Проведено численное моделирование движения вязкой несжимаемой неизотермической жидкости в открытой полости учётом её охлаждения через внешнюю границу боковой поверхности. Получены гидродинамическая картина течения жидкости и температурные профили для твёрдой и жидкой фаз. Изучено влияние условий теплообмена на характер движения теплоносителя.
Ключевые слова: сопряжённый теплоперенос, гидродинамика, технологическая полость, вязкая несжимаемая неизотермическая жидкость, численное моделирование.
Введение. Важное прикладное значение имеют процессы переноса тепла с учетом движения среды. Это обусловлено тем, что такие процессы реализуются в теплотехнических устройствах, энергетических системах и технологических процессах различных производственных циклов. Необходимость изучения режимов движения конвективных течений и сложных условий теплообмена связано с развитием энергоемких отраслей промышленности [1–6].
В данной работе рассматривается нестационарное взаимодействие жидкости с открытой полостью. Изучается процесс движения расплава металла в выемке с учётом теплообмена с её стенками. Теплофизические характеристики расплава и стенок полости идентичны. Цель данной работы — исследовать гидродинамику и сопряжённый теплообмен при движении вязкой несжимаемой жидкости в прямоугольной полости в условиях охлаждения внешней границы боковой стенки.
Изучение описанного процесса проводилось с использованием математической модели на основе системы уравнений Навье-Стокса в переменных вихрь-функция тока, уравнения энергии, уравнения теплопроводности для материала полости с соответствующими начальными и граничными условиями
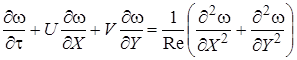 (1)
(1)
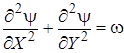 (2)
(2)
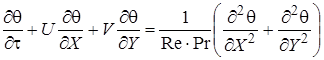 (3)
(3)
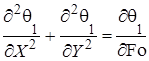 (4)
(4)
На нижней границе (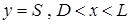 ) и боковой (
) и боковой (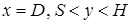 ) выставляется условие непротекания, прилипания, а также граничное условие четвёртого рода для уравнения энергии (задача решена в сопряжённой постановке).
) выставляется условие непротекания, прилипания, а также граничное условие четвёртого рода для уравнения энергии (задача решена в сопряжённой постановке).
Условия неразрывности тепловых потоков и непротеканиязаданы на линии симметрии (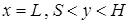 ). На участке выхода выставлялись условия «сноса» и «мягкое» граничное условие для скорости и температуры соответственно [4].
). На участке выхода выставлялись условия «сноса» и «мягкое» граничное условие для скорости и температуры соответственно [4].
На внешних границах полости заданы условия теплоизоляции, за исключением боковой области (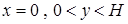 ), на которой задано граничное условие третьего рода (моделируется интенсивный теплообмен с внешней средой):
), на которой задано граничное условие третьего рода (моделируется интенсивный теплообмен с внешней средой):
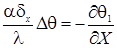 .
.
Здесь Fo — число Фурье; Re — число Рейнольдса; Pr — число Прандтля; 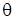 — безразмерная температура жидкости;
— безразмерная температура жидкости; 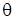 1 — безразмерная температура материала полости; X, Y — безразмерные декартовы координаты; U, V — безразмерные продольная и поперечная составляющая скорости движения жидкости соответственно; ω, ψ — переменные вихрь — функция тока; x,y — размерные декартовы координаты; L, H — линейный размер полости по координате x и y соответственно; D, S — линейный размер стенки полости по координате x и y соответственно;
1 — безразмерная температура материала полости; X, Y — безразмерные декартовы координаты; U, V — безразмерные продольная и поперечная составляющая скорости движения жидкости соответственно; ω, ψ — переменные вихрь — функция тока; x,y — размерные декартовы координаты; L, H — линейный размер полости по координате x и y соответственно; D, S — линейный размер стенки полости по координате x и y соответственно; 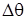 — разность безразмерных температур между внешней боковой поверхностью и окружающей средой; α — коэффициент теплоотдачи; λ — коэффициент теплопроводности; δx — толщина стенки по координате x.
— разность безразмерных температур между внешней боковой поверхностью и окружающей средой; α — коэффициент теплоотдачи; λ — коэффициент теплопроводности; δx — толщина стенки по координате x.
Решена система уравнений Навье-Стокса в переменных функция тока-вихрь, уравнение энергии и уравнение теплопроводности методом конечных разностей [4]. Разностные аналоги уравнений переноса и теплопроводности решены методом прогонки [4]. Уравнение Пуассона на каждом временном слое решалось методом последовательной верхней релаксации. Использовалась разностная схема второго порядка точности.
Вычисления выполнялись на равномерной и неравномерной разностных сетках. Оценка достоверности результатов численного моделирования проводилась проверкой консервативности использовавшейся разностной схемы аналогичным методом, применявшимся в [5, 6].
Рассматривалась жидкость разных типов (расплавленный свинец, жидкая сталь, расплав легких металлов, мазут и т. д.). На рис. 1–3 приведены типичные результаты численных исследований описанных процессов для жидкой стали.
Анализ гидродинамики течения позволяет выделить характерные области прямого (1 этап) и возвратного (2 этап) движения жидкости (рис.1).
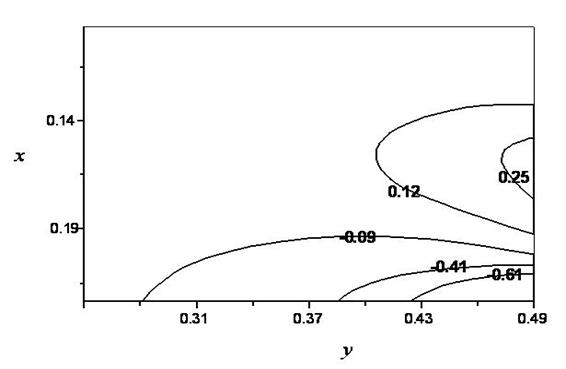
Рис. 1. Изолинии поперечной составляющей скорости в момент времени Fo=4,5∙10–2 при числе Re=300 и геометрическом отношении сторон полости L/H=1/2
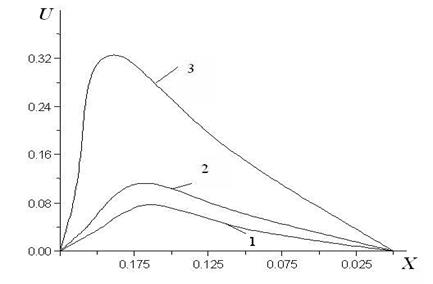
Рис. 2. Изолинии продольной составляющей скорости в момент времени Fo=4,5∙10–2 при числе Re=300 и геометрическом отношении сторон полости L/H=1/2. Кривые соответствуют значениям U(X) в сечениях: 1 — y=0.815; 2 -y=0.733; 3 — y=0.625
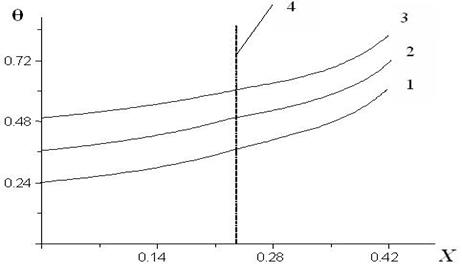
Рис. 3. Распределения температуры в твёрдой и жидкой фазах в различных сечениях y по координате x в момент времени Fo=4,5∙10–2 при Re=400, Pr=0.979 и геометрическом отношении сторон полости L/H=1/2: 1 — y=0.51; 2 — y=0.6; 3 -y=0.73; 4 — граница раздела жидкой и твёрдой фаз
С увеличением скорости затекания жидкости профиль поперечной составляющей скорости в начальных сечениях полости становится более заполненным и близким к постоянному значению (темп заполнения уменьшается на 15 % по сравнению с условиями теплоотвода через внешнюю донную поверхность).
При движении жидкости к основанию выемки поперечная составляющая скорости падает в условиях роста продольной составляющей (рис.2).
На рис.3 представлены распределения температуры в твёрдой и жидкой фазах в различных сечениях y по координате x в момент времени Fo=4,5∙102 при Re=400, Pr=0.979 и геометрическом отношении сторон полости L/H=1/2: 1 — y=0.51; 2 — y=0.6; 3 — y=0.73. Характер распределения температуры в жидкой фазе по сечениям носит более выраженный характер, чем в твёрдой. В твердой фазе температурный напор уменьшается по высоте полости, что обусловлено теплоотводом с её внешней боковой поверхности и конвективным теплопереносом в гидродинамической области.
Выводы:
Результаты численного анализа позволяют оценить влияние охлаждения внешней поверхности боковой стенки полости на условия теплообмена и гидродинамическую картину течения теплоносителя.
Проведённые исследования позволяют сделать вывод о возможности расширения области применения математического аппарата [3, 6] для решения задач сопряжённого теплообмена при движении жидкости в полостях c более сложными геометриями и условиями теплопереноса.
Литература:
1. Рыкалин Н. Н., Углов А. А., Анищенко Л. М. Высокотемпературные технологические процессы. Теплофизические основы. — М.: Наука, 1985. — 172 c.
2. Fedorov A. G., Viskanta R. Three-dimensional conjugate heat transfer in the microchannel heat sink for electronic packaging // J.Heat Mass Transfer.-2000.-№ 43.-p.399–415.
3. Kraynov A. V., Kuznetsov G. V. Conjugate heat transfer during viscous liquid movement in the open cavity, considering its cooling through outer boundary of back surface (01023) // EPJ Web of Conferences. — 2014 — Vol. 76. — p. 1–6
4. Самарский А. А., Вабищевич П. Н. Вычислительная теплопередача. — М.: Едиториал УРСС, 2003. — 784 с.
5. Kuznetsov G. V., Sheremet M. A. Modelling of non-stationary heat transfer in closed area with a local heat source // J. Thermophysics and Aeromechanics.-2005.-v.12.-№ 2.-p.287–295.
6. Kuznetsov G. V., Krainov A. V. Conjugate heat exchange and hydrodynamics for a viscous incompressible fluid moving in a rectangular cavity // J. Applied Mechanics and Technical Physics.- 2001.- v.42.- № 5.- p.851–856.







