Возможности Simulink по моделированию систем связи
Simulink является мощным пакетом программы Matlab, которой предназначен для моделирования линейных и нелинейных динамических систем. Для построения функциональной блок-схемы моделируемых устройств Simulink имеет большую библиотеку блочных компонентов и редактор блок-схем. Модель можно считать программой, которую можно просмотреть с помощью тестового редактора или с помощью редактора системы MATLAB.
У Simulink богатая библиотека компонентов, которая включает источники сигналов с практически любыми временными зависимостями, масштабирующие, линейные и нелинейные преобразователи с разнообразными формами передаточных характеристик, интегрирующие и дифференцирующие блоки и т. д.
В библиотеке имеется целый набор виртуальных регистрирующих устройств — от простых измерителей, например вольтметра или амперметра, до универсальных осциллографов, позволяющих просматривать временные зависимости выходных параметров моделируемых систем. Средства графической анимации Simulink позволяют получать наглядное представление результатов моделирования.
Описание характеристик моделируемой системы
Когда речь идет о производительности приемника подразумевается наличие некоторого уровня синхронизации сигнала. Тактовая синхронизация — это процесс установления точного временного соответствия между принимаемым сигналом и последовательностью тактовых импульсов. Тактовая синхронизация требуется в любой системе цифровой связи, которая передает информацию синхронно. Восстановление несущей требуется, если сигнал детектируется когерентно. [1]
В цифровых системах выход демодулятора должен периодически стробироваться c некоторым периодом для того, чтобы восстаносить переданную информацию. Так как время распространения от передатчика к приёмнику обычно неизвестно, управление этим стробированием должно осуществляться от принимаемого сигнала.
Рассмотрим методы обеспечения синхронизации по несущей и тактам в приемнике. Для этого рассмотрим математическую модель для сигнала на входе приемника.
Пусть канал задерживает переданные сигналы и искажает посредством аддитивного гауссовского шума. Следовательно, принимаемый сигнал можно выразить так:
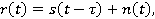
где
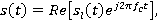
t — время задержки при распространении волны,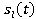
— эквивалентный низкочастотный сигнал.
Принимаемый сигнал также можно выразить:
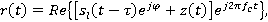
где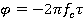 
— фаза несущей, обусловленная задержкой при распространении волны
z(t) — низкочастотный эквивалент шума.
Таким образом принимаемый сигнал можно представить так:
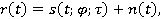
где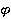 
и τ — сигнальные параметры, которые должны быть оценены.
Чтобы того, чтобы упростить обозначения, можно обозначить через ψ векторный параметр {φ,τ}.
Существуют два основных подхода, которые широко используются для оценки сигнальных параметров: подход с использованием правила максимального правдоподобия (МП) и по правилу максимума апостериорной вероятности (МАВ). В правиле МАВ сигнальный векторный параметр считается случайным и характеризуется априорной плотностью вероятности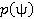 
. По правилу максимального правдоподобия сигнальный векторный параметр 
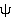трактуется как детерминированный, но неизвестный.
Формируя ортонормированное разложение r(t) по N ортонормированным функциям {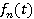
}, мы можем представить r(t) вектором коэффициентов 
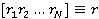. ФПВ случайных величин 
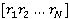можно представить условной плотностью вероятности 
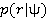. Тогда МП оценка 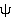— это величина, которая максимизирует 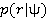. С другой стороны, оценка МАВ — это величина 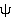, которая максимизирует апостериорную функцию плотности вероятности:
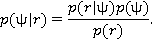
В случае, когда неизвестна априорная плотность параметра 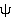, можно предположить, что 
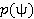равномерно распределена во всей области значений параметра. В этом случае величина 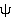,которая максимизирует 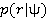, также максимизирует 
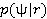. При этом оценки МАВ и МП совпадают.
В трактовке оценок параметров рассмотрим параметры φ и τ как неизвестные, но детерминированные. Поэтому для оценки используем правило МП. При такой оценке сигнальных параметров требуется, чтобы приёмник извлекал оценку путем наблюдения принимаемого сигнала на интервале времени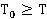 
, который называется интервалом наблюдения.
Полагая, что аддитивный шум в канале n(t) является гауссовским и белым с нулевым средним, можно совместную ФПВ 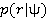выразить так:
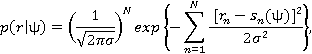
где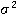 
— дисперсия случайной величины 
, 
, 
=
, 
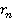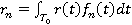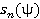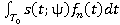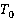— интервал интегрирования в разложени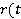и 
) и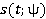 
.
Аргумент в экспоненте можно выразить через сигналы 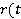) и 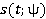. Тогда:
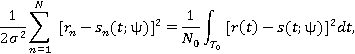
где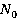 
— спектральная плотность мощности случайного процесса n(t).
Теперь максимизация 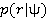, по сигнальному параметру 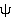эквивалентна максимизации функции правдоподобия
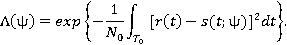
Рисунок 1 иллюстрирует блок схему демодулятора и детектора для двоичной ФМ.
Видим, что оценка фазы несущей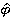 
нужна при генерировании опорного сигнала 
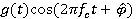для коррелятора. Синхронизатор тактов управляет стробирующим устройством и генератором сигнального импульса. В случае, когда сигнальный импульс прямоугольный, генератор сигнального импульса можно исключить.
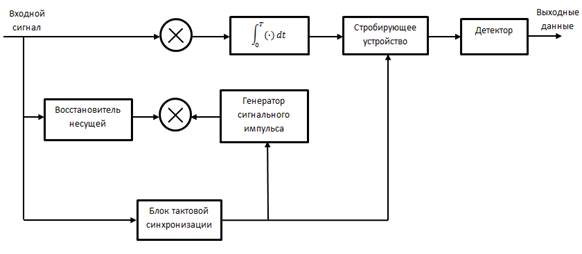
Рис. 1. Блок-схема приёмника двоичной ФМ
Блок-схема демодулятора для М-позиционной ФМ показана на рисунке 2. В этом случае требуется два коррелятора (или согласованных фильтра) для корреляции принимаемых сигналов с двумя квадратурными несущими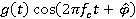 
и 
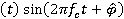, где 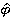-оценка фазы несущей. Фазовый детектор сравнивает фазы принимаемого сигнала с возможными к передаче фазами сигнала
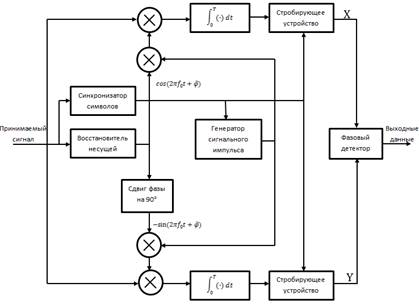
Рис. 2. Блок-схема приёмника М-позиционной ФМ
Описание модели Simulink
Реализация блок-схемы приёмника 4-позиционной ФМ (QPSK) показана на рисунке 3.
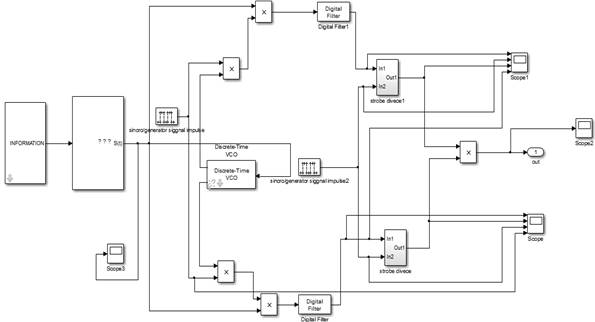
Рис. 3. Реализация приёмника 4-позиционной ФМ в Simulink
В качестве принимаемого сигнала мы используем QPSK сигнал, который формируется при помощи блоков INFORMATION и Transmitter S(t). Входным параметром блока INFORMATION является F=1/τ=20/(0.5e-6).
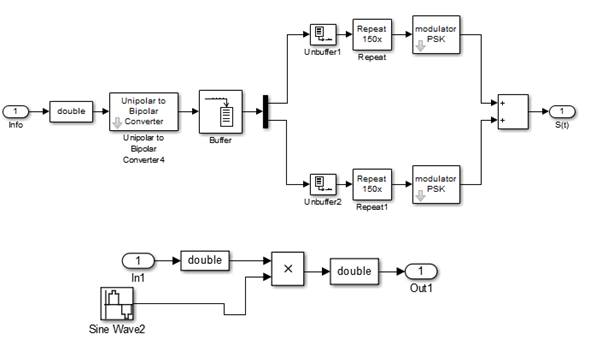
Рис. 4. Подсистемы блоков Transmitter S(t) и modulator PSK
Входным параметром блока modulator PSK является f=1/(40e6). В блок Sine Wave1 записываются следующие параметры:
- Amplitude = 1;
- Phase = 0 rad;
- Frequency = 2π* fпч= 2*pi*400e6 rad/sec;
- Sample time = 1/fнес=1/3e9 s.
А в блок Sine Wave2 (для второго modulator PSK):
- Amplitude = 1;
- Phase = pi/2 rad;
- Frequency = 2π* fпч= 2*pi*(400e6) rad/sec;
- Sample time = 1/fнес=1/3e9 s.
Полученный QPSK сигнал мы можем увидеть, используя осциллограф scope 3. Показания осциллографа изображены на рисунке 5.
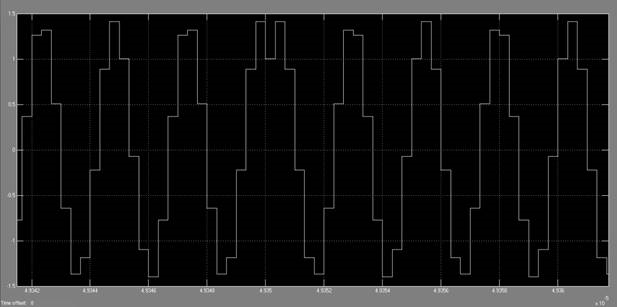
Рис. 5. QPSK сигнал
В процессе восстановления несущей мы используем блок Discrete-time VCO, подсистема которого изображена на рисунке 6. Входными параметрами данного блока являются:
- Output amplitude =1 V;
- Quiescent frequency = 400e+6 Hz;
- Input sensitivity = 10000 Hz/V;
- Initial phase = 0 rad;
- Sample time = 1/(3e+9) s.
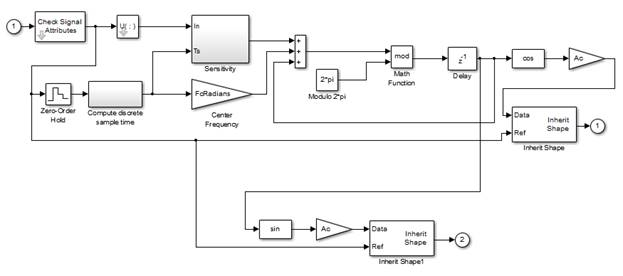
Рис. 6. Подсистема блока Discrete-time VCO
Блок sincro/generator signal impulse используется в схеме в качестве синхронизатора символов и описывается следующими параметрами:
Amplitude=1;
Period (number of samples)=20;
Pulse width (number of samples)=10;
Phase delay (number of samples)=0;
Sample time= 1/3e9.
В качестве генератора сигнального импульса мы используем блок sincro/generator signal impulse2, который описывается параметрами:
Amplitude=1;
Period (number of samples)=400;
Pulse width (number of samples)=200;
Phase delay (number of samples)=10;
Sample time= 1/3e9.
Для корреляции сигналов с двумя квадратурными несущими мы используем два согласованных фильтра, роль которых в схеме играют блоки Digital Filter и Digital Filter1. Далее сигналы подаются на входы стробирующих устройств.
Показания осциллографов scope1 и scope изображены на рисунках 7 и 8 соответственно.
Рис. 7.Показания осциллографа scope1
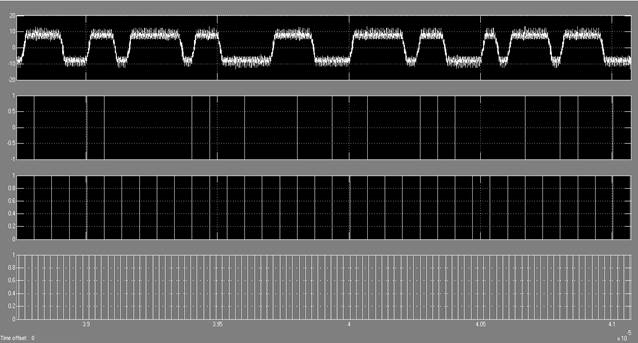
Рис. 8. Показания осциллографа scope2
Далее сравниваются фазы двух сигналов, и мы получаем сигнал на выходе приёмника, который изображен на рисунке 9.
Рис. 9. Показания осциллографа scope3
Литература:
1. Прокис Джон «Цифровая связь» М.: Радио и связь, 2000.-800 с.
2. Черных И. В. «Моделирование электротехнических устройств в MATLAB, SimPowerSystems и Simulink» М.: ДМК Пресс; СПб.: Питер, 2008. — 288 с.
