Приведен алгоритм синтеза робастного закона управления нестационарными динамическими объектами, функционирующими в условиях априорной неопределенности информации. Для синтеза нелинейных робастных алгоритмов управления предложен метод интегрального неравенства, позволяющий получить новый класс робастных законов управления. Полученный нелинейный робастный закон управления не содержит сигнальной составляющей, что значительно упрощает его реализации и обеспечивает высокие показатели качества функционирования системы управления.
Ключевые слова: робастность, нестационарность, динамический объект, неопределенность, законы управления, эталонная модель.
При разработке систем управления технологическими объектами, функционирующими в условиях априорной неопределенности, в настоящее время широко используются методы адаптивного, робастного управления, методы нечеткой логики или нейросетевых регуляторов [1]. Последнее время широкое распространения получили методы робастного управления динамическими объектами, в которых желаемая динамика выхода объекта управления задается с помощью явной или неявной эталонной моделью [2,3]. При этом целенаправленное использование нелинейностей в законе управления позволяет применить принципиально новые механизмы подавления факторов неопределенности и нестационарности объекта управления [4–6].
При создании систем управления нелинейными нестационарными динамическими объектами часто возникают трудности, связанные с априорной неопределенности информации.
Задача проектирования робастных систем управления нелинейными нестационарными объектами с различными типами запаздывающего аргумента, функционирующими в условиях априорной неопределенности, решение которой связано с разработкой сравнительно простых управляющих структур и эффективных законов управления, обеспечивающих желаемое качество процессов управления при неполном измерении элементов вектора состояний, является актуальной задачей.
Пусть объект управления задается системой дифференциальных уравнений, записанной в векторно-матричной форме:
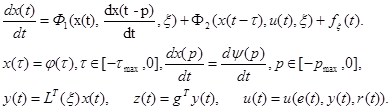 (1)
(1)
где 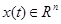 — вектор переменных состояния;
— вектор переменных состояния; 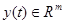 — вектор выхода объекта,
— вектор выхода объекта, 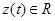 — обобщенный выход объекта; g — n-мерный вектор линейного компенсатора;
— обобщенный выход объекта; g — n-мерный вектор линейного компенсатора; 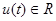 — управляющее воздействие, явный вид которого подлежит определению;
— управляющее воздействие, явный вид которого подлежит определению; 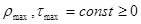 - известные запаздывания;
- известные запаздывания; 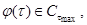
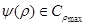 — вектор функции:
— вектор функции: 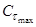 ,
,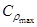 — пространства непрерывных ограниченных функций;
— пространства непрерывных ограниченных функций; 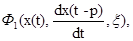
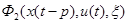 — отображения, удовлетворяющие условиям существования и единственности решения (1) при заданных начальных вектор–функциях
— отображения, удовлетворяющие условиям существования и единственности решения (1) при заданных начальных вектор–функциях 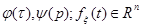 — вектор внешних возмущений или помех, который может удовлетворять неравенству вида:
— вектор внешних возмущений или помех, который может удовлетворять неравенству вида:
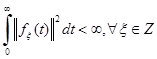 (2)
(2)
или быть ограниченным по норме
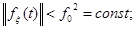
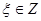 вектор неизвестных параметров;
вектор неизвестных параметров; 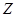 известное множество возможных значений вектора
известное множество возможных значений вектора 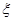 или множество, задающее класс априорной неопределенности параметров объекта управления;
или множество, задающее класс априорной неопределенности параметров объекта управления; 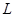 — квазипостоянная матрица заданного размера,
— квазипостоянная матрица заданного размера, 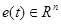 - ошибка рассогласования состояний объекта управления и эталонной модели, которая может присутствовать в системе как явно или неявно, так и явно-неявно;
- ошибка рассогласования состояний объекта управления и эталонной модели, которая может присутствовать в системе как явно или неявно, так и явно-неявно; 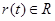 - задающее воздействие относительная степень объекта
- задающее воздействие относительная степень объекта 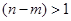 . Объект управления (1) функционирует в условиях априорной неопределенности, заданной классом
. Объект управления (1) функционирует в условиях априорной неопределенности, заданной классом 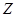 .
.
Задача управления нестационарным объектом (1) заключается в следующем: требуется построить робастную систему управления с таким управляющим воздействием 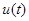 , чтобы при любом наборе
, чтобы при любом наборе 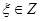 и при любых начальных условиях
и при любых начальных условиях 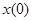 и возмущениях
и возмущениях 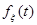 со свойствами (2) выполнялось бы целевое условие вида:
со свойствами (2) выполнялось бы целевое условие вида:
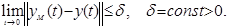
В работе предлагается метод синтеза нелинейных робастных законов управления для разных типов систем управления с нелинейными нестационарными динамическими объектами. Полученный новый класс нелинейных робастных законов управления не содержит сигнальной составляющей (знаковая функция sign), что позволяет значительно упростить реализацию робастных алгоритмов практически с высокими показателями качества функционирования систем управления.
Рассмотрим решения задачи синтеза робастного закона управления нелинейным нестационарным объектом управления, описываемый уравнениями:
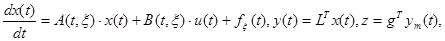 (3)
(3)
функционирующий в условиях априорной неопределенности
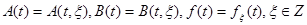 .
.
Пусть эталонная модель в системе задана неявно
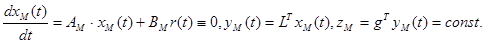 (4)
(4)
Предполагается, что выполнены следующие условия структурного согласования между объектом и эталоном:
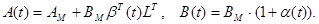 (5)
(5)
Разработка нелинейного робастного закона управления объектом в системе с неявном эталонным моделям (НЭМ) осуществляется на базе типовых этапов синтеза систем управления динамическими объектами.
Эквивалентное математическое описание исследуемой системы управления находится путем совместного преобразования уравнений объекта (3), эталона (4), а также учета условий структурного согласования (5). В результате чего получаются следующие соотношения:
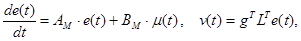 (6)
(6)
где 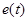 - сигнал рассогласования между объектом и эталонной моделью:
- сигнал рассогласования между объектом и эталонной моделью: 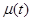 - видоизмененное управление или вход системы;
- видоизмененное управление или вход системы; 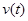 - обобщенный выход системы, формируемый за счет подбора значений вектора g в случае скалярного управления и матрицы G — в случае векторного управления.
- обобщенный выход системы, формируемый за счет подбора значений вектора g в случае скалярного управления и матрицы G — в случае векторного управления.
Для обеспечения положительности линейной стационарной части системы (6) осуществляется выбор элементов вектора или матрицы g.
Для выполнения интегрального неравенства, рассматриваемого относительно нелинейной нестационарной части системы (6), используется его модификация
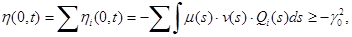 (7)
(7)
где 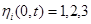 — модифицированные интегральные слагаемые вида
— модифицированные интегральные слагаемые вида
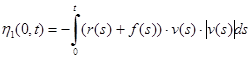 , (8)
, (8)
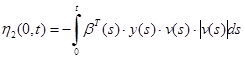 , (9)
, (9)
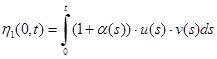 . (10)
. (10)
Выполнение (7) с учетом (8) — (10), имеет место тогда, когда нелинейный робастный закон управления синтезирован в следующем явном виде:
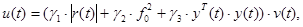
где 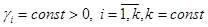 .
.
Построение нелинейных робастных законов управления для систем с явной эталонной моделью осуществляется аналогичным образом, но с учетом того, что эталонная модель входит в систему явным образом и описывается уравнениями
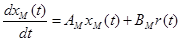 ;
;
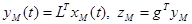 .
.
Явная эталонная модель позволяет задать желаемым образом динамику объекта управления, при этом в системе управления может использоваться эталон минимальной структурной сложности. Понижение порядка эталонной модели достигается за счет соответствующего выбора компонент вектора g и задания собственных значений матрицы 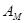 для линейной стационарной части системы с относительным порядком ее передаточной функции
для линейной стационарной части системы с относительным порядком ее передаточной функции 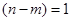 . Это позволяет сформировать явный эталонный модель в виде апериодического звена 1-го порядка, описываемого уравнением
. Это позволяет сформировать явный эталонный модель в виде апериодического звена 1-го порядка, описываемого уравнением
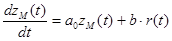
Предложенный подход реализован для синтеза нелинейного робастного алгоритма управления многодвигательным электроприводом. Результаты имитационного моделирования системы управления многодвигательным электроприводом показали, что полученный новый класс робастных законов управления позволяет обеспечить более высокое качество функционирования созданной системы.
Литература:
1. Семичевская Н. П. Нелинейное робастное управления нестационарными объектами со стационарным наблюдателем / Информатики системы управления. 2006. № 1 (11) –с.202–211.
2. Гостев В. И. Нечеткие регуляторы в системах автоматического управления. — Киев.: «Радиомотор», 2008. -972 с.
3. Баландин Д. В., Коган М. М. Алгоритмы синтеза робастного управления динамическими системами. — Нижный Новгород.: НГГУ, 2007. -88 с.
4. Поляк Б. Т., Щербаков П. С. Робастная устойчивость и управление. М.: Наука, 2002. — 239 с.
5. Siddikov I. Х. Synthesis of Neuro-Fuzzy controller for dynamic objects under conditions of uncertainty // The Advanced Science Journal. Volume 2014 Issue 2. pp.33–37.2014.
6. Сиддиков И. Х., Измайлова Р. Н., Юнусова С. Т. Алгоритм робастного управления техническим объектом, функционирующим в расплывчатых условиях // «Вестник ТГТУ» № 3–4. 2012г. –с.47–51.







