Роботы широко используются во всех отраслях промышленного производства, в домашних условиях и в сельском хозяйстве, выполняя большое количество разнообразных функций.
Роботы используются и в железнодорожной отрасли. Именно на создание робота, используемого на железной дороге, направлена наша работа.
В наше время поиск дефектов на железных дорогах очень важен, в первую очередь для безопасности передвижения поезда, целостности грузов и пассажиров.
Обнаружить такие неисправности сложно, и не всегда получается сделать это вовремя. Предлагаемый нами робот — электробалластер направлен на устранение дефектов. Он способен поставить железнодорожные пути на балластное основание при выполнении работ по строительству и техническому обслуживанию пути, проходя по ним.
Задача такого робота за короткое время выполнить дозировку балласта, предварительно выгруженного вдоль пути; срезать балласт у торцов шпал; сделать планировку откосов и междупутных зон призмы; поднять путевые решетки на формируемый балластный слой.
Конструкция электробалластера ЭЛБ-3М (Рис. 1):
расстояние между тележками 7 и 15: 30,2 м; грузоподъемность электромагнитного подъемника 440 кН; ход механизма подъема составляет 450 мм; усилена конструкция дозатора, повышенная маневренность; рельсовые и шпальные щетки снабжены электроприводом; применена четырехосная тележка.
Электробалластер ЭЛБ-3М состоит также из двух шарнирно сочлененных ферм 9 (ферма № 1) и 17 (ферма № 2), на которых смонтированы все рабочие органы. Ферма № 2 опирается на двухосную тележку (18) и четырехосную тележку (15), а ферма № 1 — на двухосную тележку (7) и междуферменный шарнир (14).
На ферме № 1 расположены кронштейн междуферменного шарнира (14), электромагнитный подъемник (13), балластерные рамы (12), механизмы сдвига пути // и подъема пути (4). У электромагнитного подъемника имеются рельсовые захваты (10), предназначенные для страховочного удержания поднятой путевой решетки при зарядке струнок n подъемке мостов. Перед тележкой № 1 установлены шпальные n рельсовые щетки (8). В хозяйственной будке (6) хранится инструмент для обслуживания механизмов электробалластера и ухода за ними. На центральном посту управления 3 находятся приборы и аппараты для управления электромагнитным подъемником и балластерными рамами
На ферме № 2 расположены кронштейн междуфермениого шарнира (14), дозатор двустороннего действия (16), машинное отделение / и пост (2) управления дозатором. Вдоль обеих ферм установлены перила (5).
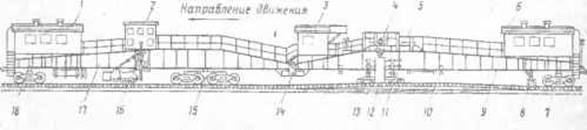
Рис.1
Благодаря наличию дифференциала поворотами робота можно управлять, изменяя скорость ω1 вращение правой полуоси: при ω1< ω2 робот поворачивает направо, при ω1>ω2 -налево. Если обычно энергия подводится к двум полуосям независимо, то в данной конструкции подвод энергии осуществлен не к левой полуоси, а к внешнему зубчатому колесу.
Это позволяет сохранить неименной величину ω2, что приводит к более равномерному движению робота.
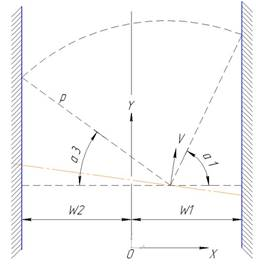
Рис. 2.
Для проведения автономного робота без столкновений с препятствиями в основу управления положен принцип «отталкивания» его от препятствий. Воображаемая «сила отталкивания» обратна расстоянию до препятствия, стремясь к бесконечности при приближении к нему в плоть до касания. Закон управления описывается следующими формулами(см. рис. 2):
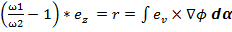 (1)
(1) 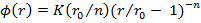 , (2)
, (2)
 Где положительные действительные величины К и n служат параметрами управления,
Где положительные действительные величины К и n служат параметрами управления, 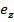 и
и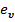 — единичные векторы в направлении оси z и скорости v соответственно, Г момент вращения относительно вертикальной оси робота,
— единичные векторы в направлении оси z и скорости v соответственно, Г момент вращения относительно вертикальной оси робота, 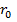 - нормальный «радиус» робота (размер зоны безопасности),
- нормальный «радиус» робота (размер зоны безопасности), 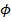 — потенциал фиктивного поля, обеспечивающего «отталкивание» от препятствий.
— потенциал фиктивного поля, обеспечивающего «отталкивание» от препятствий.
Таким образом, перемещаясь в воображаемом потенциальном поле, робот поворачивает направо при Г < 0 и налево при Г > 0.
Если обозначить 𝙙𝔁=𝙙𝒔𝜽, 𝙙𝒚=𝙙𝒔cos𝜽, (3) то можно записать 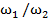 = (
= (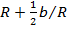 )
)
где b— расстояние между ведущими колесами робота, считая радиус кривизны левого поворота положительным, а правого — отрицательным.
Подстановка последнего выражения в управление (1) дает
Г=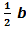 /R, (4)
/R, (4)
откуда с учетом соотношения 𝘥𝘴=-𝘙𝘥𝛳 следует 𝙙𝚹/𝙙𝙨 = -(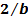 )Г(5)
)Г(5)
Траектория движения робота получается из совместного решения уравнений (1), (2), (3)и (5).
 Пусть, например, имеется прямой бесконечный коридор между двумя стенами. идеальная траектория, определяемая из уравнений (3) и (5) при Г=0, параллельна стенкам и лежит на расстоянии
Пусть, например, имеется прямой бесконечный коридор между двумя стенами. идеальная траектория, определяемая из уравнений (3) и (5) при Г=0, параллельна стенкам и лежит на расстоянии 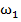 по нормали от правой стенки и на расстоянии
по нормали от правой стенки и на расстоянии 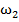 от левой стенки.
от левой стенки.
|
|
|
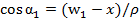 ,
, 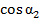 =(
=(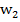 +𝑥)/𝜌, (6)
+𝑥)/𝜌, (6)
где 𝜌 — диапазон действия сенсорной системы.
Исходя из (1) и (2), можно записать
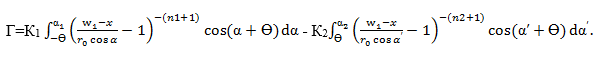 (7)
(7)
Рис. 3.
Численное решение системы (3), (5) с учетом (7) согласуется с оценками, вытекающими из теории малых возмущений. В приложении к статье приведены громоздкие выкладки. получающиеся при перемещении этой теории к выражению (7). В результате этих выкладок для случая малых отклонений, когда можно считать величины  /𝑤1, 𝜃,
/𝑤1, 𝜃, 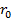 / 𝑤1 и 𝑤1/𝜌 малыми, получается отношение
/ 𝑤1 и 𝑤1/𝜌 малыми, получается отношение
Г=2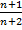 C
C 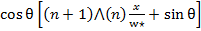 , (8)
, (8)
Где К1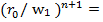 К2
К2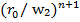 =C,
=C,
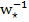 =
=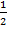
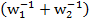 и⋀(p)=
и⋀(p)=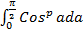 .
.
Переход к независимой переменной y с учетом равенства 𝘥𝘹/𝘥𝘺 =tg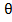 дает
дает
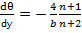 C
C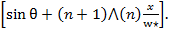 (9)
(9)
При 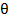 <<1 можно получить следующее линеаризованное решение:
<<1 можно получить следующее линеаризованное решение:
x =exp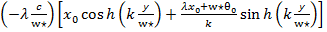 (10)
(10)
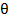 =exp
=exp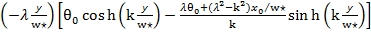 (11)
(11)
где параметры 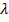 и k определяются отношениями
и k определяются отношениями 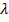 =2
=2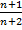 C
C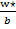 ,
, 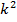 =
=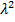 -2(n+1)⋀(n)
-2(n+1)⋀(n)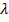 .
.
Из последнего уравнения видно, что при
С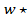 /b<(n+2) ⋀(n) (12) kявляется мнимой величиной.
/b<(n+2) ⋀(n) (12) kявляется мнимой величиной.
Если, например, положить 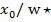 =0,1,
=0,1, 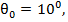 n=1 (т. е. ⋀(n) = 1), то траекторией для
n=1 (т. е. ⋀(n) = 1), то траекторией для 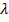 =2,4,8 примут вид, показанный на рис. 4, который демонстрирует, что при мнимом k(для
=2,4,8 примут вид, показанный на рис. 4, который демонстрирует, что при мнимом k(для 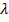 =2) возврат к идеальному маршруту происходит хуже, чем при действительном (для
=2) возврат к идеальному маршруту происходит хуже, чем при действительном (для 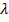 =8) и при нулевом (для
=8) и при нулевом (для 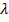 =4) значениях k.
=4) значениях k.
|
При выборе параметров К и n закона управления (1)-(2) целесообразно воспользоваться следующими соображениями:
а) поскольку величина момента Г обратно пропорциональна 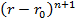 , т. е. влияние препятствия экспоненциально затухает с расстоянием, желательно уменьшать
, т. е. влияние препятствия экспоненциально затухает с расстоянием, желательно уменьшать 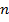 , чтобы робот не был слишком «близоруким»;
, чтобы робот не был слишком «близоруким»;
б) коэффициент К следует выбирать малым, чтобы предотвратить возникновение слишком больших центробежных сил при резких поворотах;
в) желательно избегать мнимых значений k(см. рис.4)-это определяет ограничения снизу на величину К и с учетом неравенства (12) требует малых значений 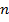 ;
;
г) очень важно упростить расчетные формулы с целью ускорения вычислений.
В соответствии с этим обычно выбирают значения 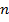 , равные 1 или 2, и k=0. При этом уравнение (10) и (11) сводятся к виду
, равные 1 или 2, и k=0. При этом уравнение (10) и (11) сводятся к виду
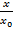 =
=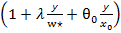 exp
exp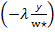
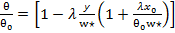 exp
exp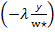 ,
,
где 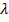 =2(
=2(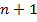 )⋀ (n).
)⋀ (n).
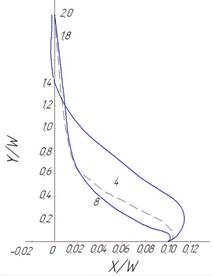
Рис. 4.
Для иллюстрации описанного метода управления движением робота в «потенциальном поле» приведены результаты машинного моделирования двух задач предотвращения столкновения мобильных роботов с препятствиями. Первая возникает при движении двух мобильных роботов на встречу друг другу в длинном узком коридоре с параллельными стенками. Вторая соответствует резкому повороту робота в Г-образном коридоре. В обоих случаях расположение стенок роботам априорно неизвестно, а расстояние до препятствий роботы определяют с помощью своих сенсорных систем.
На рис. 5 показаны траектории, полученные при модельном решении первой задачи в предположении, что роботу предложен формулами одинаковый и идеальный маршрут каждого из них в отдельности соответствуют значениям 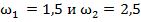 . Диапазон действия сенсоров роботов р=6; параметры управления
. Диапазон действия сенсоров роботов р=6; параметры управления 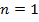 и
и 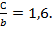
Решение второй задачи демонстрируется на рис.6, где принято 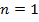 , р=6,
, р=6, 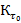 /b=9. Видно, что поворот робота происходит по достаточно плавной траектории.
/b=9. Видно, что поворот робота происходит по достаточно плавной траектории.
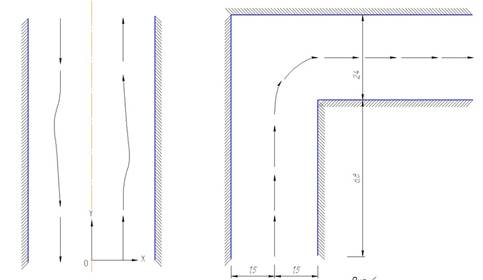
Рис. 5.
|
|
||||
Вывод
Применение современных промышленных роботов увеличивает производительность, заменяет человека на монотонных и тяжелых работах, помогает экономить материалы и энергию.
Значимость промышленных роботов не в замене человека при обслуживании известных машин. Они явились тем недостающим звеном, которое позволило объединять разрозненное технологическое оборудование в комплексные гибкие автоматизированные производственные системы машин и приборов. Именно таким системам принадлежит будущее.
Литература:
1. Поезжаева Е. В. Промышленные роботы: учебное пособие:в 3 ч.:Часть 2. Пермь Изд-во Пермского гос.техн.ун-та. 2009г. 185 с.с илл.
2. «Балластировочные, щебнеочистительные машины и хоппер — дозаторы» Соломонов С. А. М.: Транспорт, 1991. 336 с.







