При многолетнем изучении полугрупп натуральных чисел было замечено, что при сложении двух коммутативных полугрупп натуральных чисел, замкнутых относительно сложения, в результате сложения aN+bN(если a =2, а b-любое нечетное натуральное число) мы получаем НОД(a,b)\{все нечетные натуральные числа до b}.
Давайте разберемся, есть ли какая-нибудь закономерность для вычисления множества исключений при сложении полугрупп натуральных чисел, где a- нечетное число; b-нечетное число, a-четное число; b-четное число,a-четное число;b-нечетное число, и, по возможности, установим ее.
Сначала же дадим определение полугруппы, натуральных чисел и бинарной операции.
Полугруппа — множество с заданной на нем ассоциативной бинарной операцией.
Бинарной операцией на множестве S называется отображение множества всех упорядоченных пар (x, y) элементов из S в множество S, то есть правило, сопоставляющее любой такой паре вполне определенный элемент из S — результат применения данной операции к x и y. В зависимости от выбора символа для обозначения операции указанный результат обозначается как x + y, x + y, x " y, x ╒ y, x ╥ y и т. п. Операция + называется ассоциативной, если она удовлетворяет тождеству ассоциативности (по школьной терминологии, сочетательному закону): для любых x, y, z
(x + y) + z = x + (y + z).
Полугруппой называется всякое множество с заданной на нем бинарной ассоциативной операцией. Полугруппа S с операцией + называется коммутативной, если для любых x, y k S
x + y = y + x.
Если полугрупповая операция обозначена знаком + [знаком " или отсутствием знака], то ее называют сложением [умножением] и говорят об аддитивной [мультипликативной] полугруппе.
Натуральные числа (естественные числа) — числа, возникающие естественным образом при счёте. Последовательность всех натуральных чисел, расположенных в порядке их возрастания, называется натуральным рядом.
Существуют два подхода к определению натуральных чисел — это числа, возникающие при:
- подсчёте (нумерации) предметов (первый, второй, третий, …);
- обозначении количества предметов (нет предметов, один предмет, два предмета, …).
В первом случае ряд натуральных чисел начинается с единицы, во втором — с нуля. В подавляющем большинстве российских источников традиционно принят первый подход, то есть ноль не считается натуральным числом. Второй подход встречается у некоторых зарубежных авторов — например, он принят в трудах Бурбаки, где натуральные числа определяются как мощности конечных множеств. Кроме того, отсчёт с нуля широко распространён в программировании (например, для индексации массивов, нумерации битов машинного слова и т. д.).
Отрицательные и нецелые (рациональные, вещественные, …) числа к натуральным не относятся.
Множество всех натуральных чисел принято обозначать символом  (от лат. naturalis — естественный). Множество натуральных чисел является бесконечным, так как для любого натурального числа
(от лат. naturalis — естественный). Множество натуральных чисел является бесконечным, так как для любого натурального числа 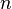 найдётся натуральное число, большее чем
найдётся натуральное число, большее чем 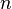 .
.
Примеры коммуникативных полугрупп натуральных чисел, замкнутых относительно сложения:
3  +7; 4
+7; 4 +11
+11 ; 2
; 2 +5
+5 и т. д.
и т. д.
Обратимся к истории исследования полугрупп натуральных чисел.
«За годы изучения этой темы опубликовано более 600 статей и более 500 тезисов докладов на различных конференциях, главным образом всесоюзных и международных. При этом более 270 статей напечатано в центральных отечественных математических журналах, более 130 — в международных журналах или трудах международных конференций, более 110 — в «Математических записках Уральского университета» (выходивших в 60–80-х годах). Отмечу обобщающие публикации по областям исследований, которым в семинаре уделялось особенно большое внимание и в которые участники семинара внесли заметный (а в некоторых вопросах — определяющий) вклад. Это обзорные статьи [6]- [13], а также монографии [14] и [15]; вторая из монографий представляет собой не просто английский перевод, а модифицированную и расширенную версию первой. Несколько из упомянутых обзорных статей, как непосредственно видно по их названиям, посвящены проблематике тождеств и другим аспектам теории многообразий. В указанных трудах обозреваются все основные достижения в соответствующих областях, принадлежащие многочисленным авторам из разных стран. Глава [16] справочной монографии по общей алгебре посвящена алгебраической теории полугрупп в целом и дает имеющий энциклопедический характер развернутый очерк этой теории (включая приложения к теориям формальных языков, автоматов и кодов) по состоянию на начало 90-х годов. Аналогичный характер имеют более ранние публикации автора данной заметки в Большой советской энциклопедии (3-е изд.) и пятитомной Математической энциклопедии (1977–1985): для первой была написана статья «Полугруппа», для второй — цикл из 40 статей по теории полугрупп. Недавно несколькими участниками семинара (М. В. Волковым, А. П. Замятиным и И. О. Коряковым) под руководством и при участии автора данной заметки подготовлен цикл из 11 статей для однотомной энциклопедии «Дискретная математика», выход которой в 2001 году.
Помимо оригинальных публикаций, определенное внимание было уделено нами и переводам на русский язык нескольких фундаментальных зарубежных трудов в областях, входящих в круг интересов участников семинара. Это двухтомная монография [17], основным переводчиком которой был В. А. Баранский (он перевел 11 глав из 12, одна глава переведена В. Г. Житомирским), монография [18] и учебное пособие [19], переведенные И. О. Коряковым»., — по Л. Н. Шеврину.
Автором данной статьи были проведены некоторые эксперименты, которые будут приведены ниже.
Пусть a=3, b=7, тогда
3 +7
+7 =\
=\ {1,2,4,5,8,11};
{1,2,4,5,8,11};
Пусть a=5, b=7, тогда
5 +7
+7 =
= \{1,2,3,4,6,8,9,11,13,16,18,23};
\{1,2,3,4,6,8,9,11,13,16,18,23};
Пусть a=4, b=5, тогда
4 +5
+5 =\
=\ {1,2,3,4,6,7,11};
{1,2,3,4,6,7,11};
Пусть a=2, b=4, тогда
2 +4
+4 =2
=2 ;
;
Пусть a=11, b=7, тогда
11 +7
+7 =\
=\ {1,2,3,4,5,6,8,9,10,12,13,15,16,17,19,20,23,24,26,27,30,31,34,37,38,41,45,48,52, 59};
{1,2,3,4,5,6,8,9,10,12,13,15,16,17,19,20,23,24,26,27,30,31,34,37,38,41,45,48,52, 59};
Пусть a=2, b=5, тогда
2 +5
+5 =
= \{1,3};
\{1,3};
Пусть a=2, b=11, тогда
2 +11
+11 =
= \{1,3,5,7,9}.
\{1,3,5,7,9}.
Результаты исследования.
При сложении двух коммутативных полугрупп натуральных чисел, замкнутых относительно сложения, в результате сложения aN+bN(если a =2, а b-любое нечетное натуральное число) мы получаем НОД(a,b)\{все нечетные натуральные числа до b}.
При сложении двух коммутативных полугрупп натуральных чисел, замкнутых относительно сложения, в результате сложения aN+bN(если a — четное натуральное число, а b- четное натуральное число) мы получаем НОД(a,b)\пустое множество.
Для вычисления результата сложения двух коммутативных полугрупп натуральных чисел, где а — нечетное число, а b — четное число и а,b — нечетные числа мною выведен алгоритм, который я приведу ниже.
Алгоритм.
1. Сумма будет равна НОД (а,b).
2. Во множество исключений войдут: все числа, меньшие меньшего из чисел а и b.
Например, если а < b,то все числа, меньшие а.
3. Определяем наибольшее число множества исключений по формуле:
m(искомое число)= аb-(a+b).
4. Сравниваем числа: b, a+b, 2a. Вписываем во множество исключений все числа, большие а, но меньшие меньшего их этих чисел.
Например, если b — наименьшее из этих чисел, то во множество исключений войдут все числа, большие а (т. к. а < b), но меньшие b.
5. Поочередно вычитаем из числа m: a nраз, b dраз, a+bc раз,(где n, d, c — любые числа), пока в результате вычитания мы не получим одно из полученных ранее нами чисел.
Например, пусть a=5, b=7, тогда
5 +7
+7 =\
=\ {1,2,3,4,6,8,9,11,13,16,18,23};
{1,2,3,4,6,8,9,11,13,16,18,23};
Где 1,2,3,4-числа, меньшие а; 6- число между a и b (т. к. в данном случае b — наименьшее из чисел a+b, 2а, b); 8, 9, 11, 13, 16,18 — результаты поочередного вычитания из наибольшего числа множества исключений чисел a nраз, b dраз, a+bc раз,(где n, d, c — любые числа); 23 — наибольшее число множества исключений, выведенное по приведенной выше формуле.
Из приведенных выше экспериментов, полученных результатов был выведен алгоритм вычисления множества исключений при сложении коммутативных полугрупп натуральных чисел, замкнутых относительно сложения. Этот алгоритм в несколько раз облегчает процедуру поиска множества исключений и считанными операциями ограничивает область поиска исключений. Выведением данного алгоритма решается одна из многочисленных задач, возникающих при тщательном изучении полугрупп натуральных чисел, но, тем не менее, нерешенных задач, с каждым днем становится все больше, а вопросы, не имеющие в настоящее время ответов, становятся все сложнее и сложнее. Автор данной статьи выражает надежду на то, что методом подобных исследований и экспериментов с течением времени ученым все-таки удастся найти правильные ответы на эти вопросы.
Литература:
1. https://ru.wikipedia.org/wiki/ %D2 %E5 %EE %F0 %E5 %EC %E0_ %D4 %F0 %EE %E1 %E5 %ED %E8 %F3 %F1 %E0
2. http://dxdy.ru/topic9137.html
3. http://enc-dic.com/enc_math/Perrona---frobeniusa-teorema-3104.html







