В данной статье разобраны алгоритмы шифрования и дешифрования текста шифром Цезаря и шифром Хилла, а также описывается Windows-приложение, реализующее данные алгоритмы.
Ключевые слова:шифрование, дешифрование, шифр Цезаря, шифр Хилла, криптология.
Введение
Описание алгоритмов шифров Цезаря и Хилла
Люди стали использовать шифрование еще с древних времен, когда появилась первая секретная информация. Один из самых первых и известных шифров — это шифр Цезаря. Он использовал простейший метод шифрования, смысл которого заключается в том, чтобы каждая буква заменялась буквой на три позиции дальше по алфавиту. Правило шифрования будет выглядеть следующим образом: «А» заменяется на «Г», «Б» заменяется на «Д», «В» заменяется на «Е» и так далее. В свою очередь, «Ь» заменяется на «Я», а буква «Э» заменится на «А» и снова по кругу. Также всю полезную информацию о данном шифре можно найти в [2] и [4].
Шифр Хилла — это шифр подстановки, основанный на законах линейной алгебры и изобретенный в 1929 году Лестером С. Хиллом. Алгоритм данного шифра состоит в следующем: для начала следует пронумеровать исходный алфавит. Алфавитом считаются не только буквы, но и символы, причем заглавная буква «А» будет отличаться от прописной буквы «а». Полученное количество букв и символов далее будет называться модулем. Например, в русском алфавите из заглавных букв модуль будет равен 33. Ниже в примере будет рассматриваться именно этот алфавит. Таким образом, сегмент из 33 номеров можно представить в виде некоторого вектора v1. Следующий шаг — составление ключевой матрицы C. При этом матрица может быть любого размера, только следует помнить, что, чем больше матрица, тем сложнее расшифровывать текст и, соответственно, наоборот. Также следует избегать нулей в ключевой матрице — это способствует быстрой расшифровке, а значит, такой шифр гораздо легче взломать. Еще один из очень важных пунктов, которые не следует забывать: ключевая матрица должна быть обратимой, иначе расшифровка текста будет невозможной. Стоит, к тому же, проверить, чтобы модуль алфавита и определитель ключевой матрицы не имели никаких общих делителей, кроме единицы. Затем матрица C умножается на вектор v1 по модулю 33. Проблема данного шифра заключается в том, что на все известные языки мира составлена статистика частоты встречаемости каждой буквы, что, несомненно, сильно упрощает расшифровку текста, не зная при этом ключевой матрицы. Особенности шифра Хилла можно найти в [1] и [3].
Для лучшего понимания шифровки и дешифровки текста ниже разобран пример.
Рассмотрим слово «МОСКВА». Оно делится на два блока по три буквы: «МОС» и «КВА». Блоку «МОС» соответствует вектор v1 = (14, 16, 19), а блоку «КВА» — вектор v2 = (12, 3, 1).
Ключом данного шифра будет матрица С (которая необходима для шифрования) размерностью 3*3, т. е. n = 3:
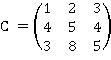
Обратной матрицей по модулю 33 будет матрица D (которая необходима для расшифровки):
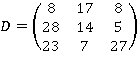
Тогда C*v1 = (103, 212, 265), a C*v2 = (21, 67, 65).
Полученные значения следует разделить на 33 и записать остаток — он и будет зашифрованным сообщением.
(103 mod 33, 212 mod 33, 265 mod 33) = (4, 14, 1), что соответствует вектору «ГМА».
(21 mod 33, 67 mod 33, 65 mod 33) = (21, 1, 32), что соответствует вектору «УАЮ».
Таким образом, вместо слова «МОСКВА» мы получили слово «ГМАУАЮ».
Расшифруем данное сообщение:
w1 = (4, 14, 1), тогда D*w1 = (278, 313, 217), а w2 = (21, 1, 32), и D*w2 = (441, 762, 1354).
(278 mod 33, 313 mod 33, 217 mod 33) = (14, 16, 19) — это и есть блок «МОС».
(441 mod 33, 762 mod 33, 1354 mod 33) = (12, 3, 1) — а это блок «КВА».
Итак, в ходе дешифровки получилось исходное слово «МОСКВА». Так как после дешифрования получилось слово, которое и было зашифровано, то можно сказать, что шифрование было выполнено верно.
Описание разработанного приложения
Приложения, реализующего шифрование и дешифрование текста шифром Цезаря и шифром Хилла, в общем доступе обнаружено не было. Следовательно, данное приложение будет одним из первых в своем роде. Поэтому приложение должно быть дружелюбным и интуитивно простым в использовании, чтобы каждый среднестатистический пользователь компьютера мог самостоятельно работать в нем. Для быстрого и удобного шифрования и дешифрования текста было разработано приложение, реализующее алгоритмы шифров Цезаря и Хилла только на стационарных компьютерах.
Приложение получает на вход:
1. Текстовое сообщение (на русском языке с использованием знаков препинания).
2. Шифр на выбор пользователя: либо шифр Цезаря, либо шифр Хилла.
3. Действие на выбор пользователя: либо шифрование, либо дешифрование.
4. Если пользователем был выбран шифр Цезаря, то пользователь также должен ввести величину сдвига (максимальный размер которого 6 знаков).
5. Если пользователем был выбран шифр Хилла, то пользователь также должен ввести размерность ключевой матрицы (максимальный размер матрицы равен 9*9) и саму матрицу (члены которой имеют максимальный размер 3 знака).
6. Результатом работы приложения будет являться зашифрованная строка.
Для получения наиболее удобного в использовании интерфейса было разработано две формы, которые показаны на рисунках 1 и 2. Также на рисунках 1, 2 и 3 показаны примеры результата работы приложения.
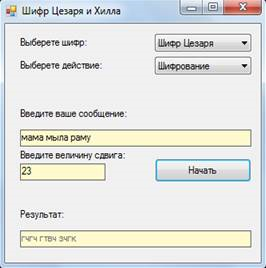
Рис. 1. Пример работы шифрования текста шифром Цезаря
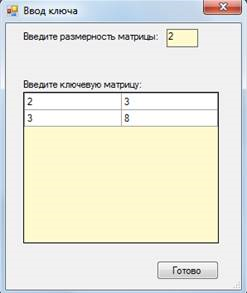
Рис. 2. Пример ввода ключевой матрицы для шифра Хилла
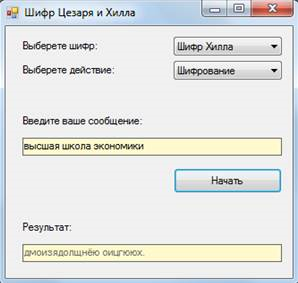
Рис. 3. Пример работы шифрования текста шифром Хилла
Итогом работы стало приложение, выполняющее шифрование и дешифрование текста шифром Цезаря и шифром Хилла.
Для разработки данного приложения были изучены такие разделы линейной алгебры как обратный элемент в кольце по модулю, расширенный алгоритм Евклида, нахождение обратной матрицы по модулю, к тому же были разобраны методы работы с WindowsForms, библиотекой Math.NetNumerics и листами, а также отработаны навыки программирования, алгоритмизации и проектирования интерфейса.
Данное приложение можно улучшить, если добавить возможность выбирать файлы для шифрования. Дополнительно можно добавить модернизированные виды шифров, а также новые шифры, возможность шифрования текста не только на русском языке, но и на других языках мира.
1. Шифр Хилла. // Проект КРИПТО-NNN. [Электронный ресурс]. [Режим доступа: http://crypto.hut2.ru/hill.html] [Проверено: 12.03.2015]
2. Worbst R. Cryptology Unlocked Translated by Angelika Shafir, 2007. — 557 с.
3. Шифр Хилла. // Академик. [Электронный ресурс]. [Режим доступа: http://dic.academic.ru/dic.nsf/ruwiki/1346299#.D0.9F.D1.80.D0.B8.D0.BC.D0.B5.D1.87.D0.B0.D0.BD.D0.B8.D1.8F] [Проверено: 9.03.2014]
4. Dennis L. Cryptology: From Caesar Ciphers to Public-Key Cryptosystems, 1997. — 17c.







