Рассматриваются вопросы оптимизации кода для многопроцессорных систем на базе концептуально нового поколения вычислительной техники — нейрокомпьютеров, принцип функционирования которых основан на принципах мышления человека. Показана методология разбиения программы на множество подпрограмм, загружаемых на нейропроцессорный вычислительный модуль системы.
Ключевые слова: нейрокомпьютер, оптимизация, распараллеливание, обработка информации, программа.
Введение. Программирование нейрокомпьютера — это обучение его на выполнение той или иной задачи, в связи с чем известные методы оптимизации и распараллеливания нейрокомпьютерной программы не могут быть ипользованы [1]. В свою очередь, интерес же к нейрокомпьютерам и нейрокомпьютерным системам постоянно увеличивается, их применяют в различных сферах: космос, военная промышленность, дорожное движение и др., в связи с чем, возникает необходимость разработки математического, алгоритмического и программного обеспечения создания и оптимизации программ для нейрокомпьютеров и систем на их базе. Следует также отметить, что нейрокомпьютерные системы обладают очень высоким уровнем распараллелирования, в связи с чем наиболее важна задача именно распараллеливания и оптимизации вычислительных систем на базе нейропроцессорных устройств [1–3].
Цель работы: разработка математического аппарата программной оптимизации в вычислительных системах различной структуры на базе нейропроцессоров.
Пусть 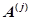 — некоторый
— некоторый 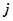 -й алгоритм обработки информации для реализации его на на нейропроцессорной платформе. Введем множество операций
-й алгоритм обработки информации для реализации его на на нейропроцессорной платформе. Введем множество операций 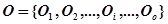 . С учетом введенного множества операций этот алгоритм обработки информации представляет собой кортеж, состоящий из операций
. С учетом введенного множества операций этот алгоритм обработки информации представляет собой кортеж, состоящий из операций 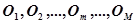 длиной
длиной 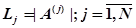 , т. е.:
, т. е.:
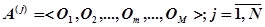 . (1)
. (1)
Исходя из математического смысла нейрокомпьютерной обработки множество операций нейрокомпьютера рационально разделить на 2 подмножества [4–11]:
1. Множество операций первого типа, представляющих математическую модель формального нейрона, и состоящее из одной операции 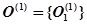 :
:
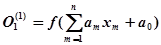 (2)
(2)
Операция 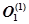 может быть рассмотрена в виде множества самостоятельных операций исходя из функциональных блоков, ее реализующих:
может быть рассмотрена в виде множества самостоятельных операций исходя из функциональных блоков, ее реализующих:
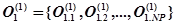 , (3)
, (3)
где 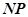 — количество возможных видов векторных операций эмуляции нейрона в нейропроцессоре.
— количество возможных видов векторных операций эмуляции нейрона в нейропроцессоре.
2. Множество вспомогательных операций второго типа: обмена данными, управления подготовки данных, и др.
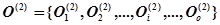 (5)
(5)
Тогда алгоритм (1) можно записать следующим образом:
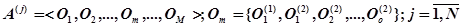 (6)
(6)
На этапе разработки программы каждой операции ставится в соответствие микрокоманда процессора 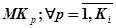 , где
, где 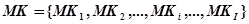 - множество микрокоманд, написанных на внутреннем языке нейропроцессора;
- множество микрокоманд, написанных на внутреннем языке нейропроцессора; 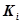 - минимальное количество микрокоманд, необходимое для реализации операции
- минимальное количество микрокоманд, необходимое для реализации операции 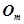 .
.
Множество микрокоманд также можно разделить на 2 подмножества:
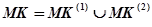 , (7)
, (7)
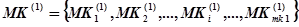 , (8)
, (8)
где 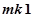 — число сочетаний исходя из (3) для конкретного нейропроцессора. Для того, чтобы определить
— число сочетаний исходя из (3) для конкретного нейропроцессора. Для того, чтобы определить 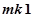 , необходимо найти количество сочетаний команды притом, что часть функциональных блоков и часть может быть незадействована, т. е. количество возможных вариантов, если задействован один функциональный блок, если два, и т. д.:
, необходимо найти количество сочетаний команды притом, что часть функциональных блоков и часть может быть незадействована, т. е. количество возможных вариантов, если задействован один функциональный блок, если два, и т. д.:
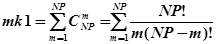 , (9)
, (9)
где 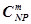 — число сочетаний из
— число сочетаний из 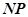 элементов по
элементов по 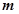 .
.
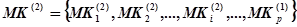 , (10)
, (10)
где 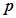 — количество возможных микрокоманд, возможных для реализации вспомогательных операций второго типа, определяемых согласно (5).
— количество возможных микрокоманд, возможных для реализации вспомогательных операций второго типа, определяемых согласно (5).
Тогда, для каждой операции первого типа:
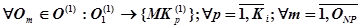 , (11)
, (11)
Под программой 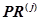 понимается кортеж микрокоманд:
понимается кортеж микрокоманд:
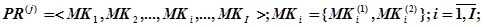 , (12)
, (12)
длиной 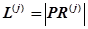 .
.
В данном пункте на основании алгебраического подхода предлагается методика разбиения программы 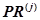 на множество подпрограмм
на множество подпрограмм 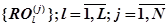 исходя из числа нейропроцессорных вычислительных модулей (НПВМ)
исходя из числа нейропроцессорных вычислительных модулей (НПВМ) 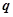 [78].
[78].
Исходя из специфики и принципов функционирования нейрокомпьютеров, количество команд 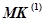 гораздо больше команд
гораздо больше команд 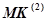 (не превышает 1 %), более того команды второго типа «делят» кортеж микрокоманд на сегменты, так как являются вспомогательными для подготовки данных (рисунок 1).
(не превышает 1 %), более того команды второго типа «делят» кортеж микрокоманд на сегменты, так как являются вспомогательными для подготовки данных (рисунок 1).

Рис. 1. Сегменты программы для нейрокомпьютера
Исходя из принципов функционирования и назначения нейрокомпьютера, количество и вид команд 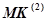 зависит от кортежа команд
зависит от кортежа команд 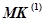 , то есть каждая, произвольно взятая команда
, то есть каждая, произвольно взятая команда 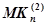 зависит от некоторой команды
зависит от некоторой команды 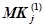 то есть:
то есть:
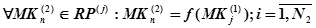 , (13)
, (13)
где 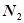 — количество операций второго типа. Также, каждой операции
— количество операций второго типа. Также, каждой операции 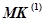 может соответствовать одна или несколько операций
может соответствовать одна или несколько операций 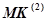 , подготавливающих данные. Поэтому, в дальнейших рассуждениях считаем команды
, подготавливающих данные. Поэтому, в дальнейших рассуждениях считаем команды 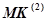 невлияющими на функционирование нейропроцессорной системы и не рассматриваем отдельно.
невлияющими на функционирование нейропроцессорной системы и не рассматриваем отдельно.
Рассмотрим отношение двух произвольно взятых микрокоманд 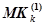 и
и 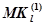 , каждая из которых представляет собой комплекс несвязанных между собой команд
, каждая из которых представляет собой комплекс несвязанных между собой команд 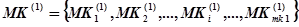 , число которых зависит от конкретного нейрокомпьютера. При этом, рассматривая две команды в виде «черного ящика», имеем:
, число которых зависит от конкретного нейрокомпьютера. При этом, рассматривая две команды в виде «черного ящика», имеем:
- одинаковое функциональное назначение — эмуляция нейрона;
- одинаковое время выполнения команды, равное одному такту нейропроцессора;
- воздействие на один и тот же набор аппаратных ресурсов;
- аппаратная реализация нейрокомпьютера предполагает один и тот же путь потока данных и потока команд.
Введем понятие функционального равенства микрокоманд 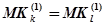 , под которым будет подразумеваться равенство времени исполнения команды
, под которым будет подразумеваться равенство времени исполнения команды 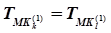 и равенство используемых командой аппаратных ресурсов
и равенство используемых командой аппаратных ресурсов 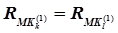 , т.е:
, т.е:
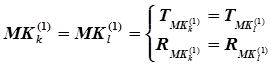 . (14)
. (14)
Тогда справедливо утверждение о том, что отношение 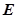 двух произвольно взятых микрокоманд
двух произвольно взятых микрокоманд 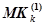 и
и 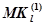 ,удовлетворяющим (14), есть отношение эквивалентности.
,удовлетворяющим (14), есть отношение эквивалентности.
Отношение эквивалентности — это бинарное отношение, для которого выполнены следующие условия: рефлексивность, симметричность, транзитивность.
Рассмотрим каждое из этих условий:
1. Всякая микронейрокоманда 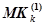 , удовлетворяющая (14), и являющаяся отражением модели нейрона, может выполняться параллельно самой себе, что подразумевает сама архитектура нейросети и нейрокомпьютера, т. е.
, удовлетворяющая (14), и являющаяся отражением модели нейрона, может выполняться параллельно самой себе, что подразумевает сама архитектура нейросети и нейрокомпьютера, т. е. 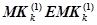 . Таким образом, справедливо условие рефлективности команд
. Таким образом, справедливо условие рефлективности команд 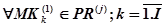 .
.
2. Если команда 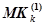 , функционально равна команде
, функционально равна команде 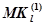 , то и команда
, то и команда 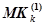 функционально равна команде
функционально равна команде 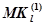 и одновременно с ней может выполняться, что предполагается исходя из парадигмы нейрокомпьютинга т. е.:
и одновременно с ней может выполняться, что предполагается исходя из парадигмы нейрокомпьютинга т. е.:
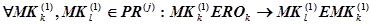 . (15)
. (15)
Другими словами выполняется условие симметричности двух нейромикрокоманд.
3. Если команда 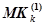 функционально равна команде
функционально равна команде 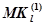 , а команда
, а команда 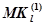 функционально равна
функционально равна 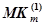 , тогда команда
, тогда команда 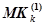 функционально равна
функционально равна 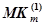 и параллельна команде
и параллельна команде 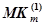 , т. е.
, т. е.
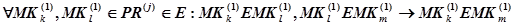 . (16)
. (16)
Таким образом, справедливо условие транзитивности нейромикрокоманд.
Введем понятие сегмента 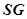 нейромикропрограммного кода, поразумевающего кортеж команд
нейромикропрограммного кода, поразумевающего кортеж команд 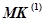 и связанных вспомогательных команд подготовки данных
и связанных вспомогательных команд подготовки данных 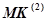 :
:
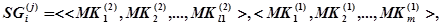
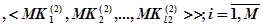 (17)
(17)
Тогда всю программу 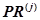 можно разделить на кортеж сегментов:
можно разделить на кортеж сегментов:
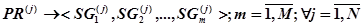 (18)
(18)
Под подпрограммой нейропрограммы 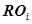 будем понимать кортеж сегментов:
будем понимать кортеж сегментов:
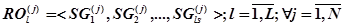 (19)
(19)
На рисунке 2 показано сегментирование и программы 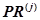 .
.
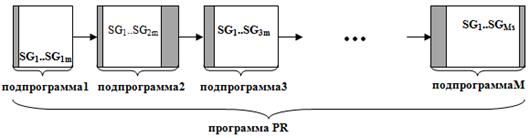
Рис. 2. Сегментирование программы 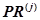
Рассмотрим две произвольно взятые подпрограммы 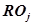 и
и 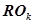 , каждая из которых представляет собой некоторый сегмент (рисунок 2), то есть представляет собой множество команд эмуляции нейрона, каждая из которых эквивалентна другой, произвольно выбранной команде, и вспомогательные команды, подготавливающие данные для обработки и являющиеся неотъемлимой частью множества команд первого типа:
, каждая из которых представляет собой некоторый сегмент (рисунок 2), то есть представляет собой множество команд эмуляции нейрона, каждая из которых эквивалентна другой, произвольно выбранной команде, и вспомогательные команды, подготавливающие данные для обработки и являющиеся неотъемлимой частью множества команд первого типа:
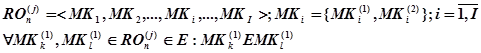 . (20)
. (20)
Рассмотрим отношение 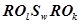 структуры
структуры 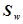 , которое указывает на то, что любые две произвольно взятые подпрограммы
, которое указывает на то, что любые две произвольно взятые подпрограммы 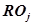 и
и 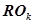 , удовлетворяющие (17), могут выполняться одновременно на разных НПВМ под управлением микрокоманд, принадлежащих указанным подпрограммам, т. е.:
, удовлетворяющие (17), могут выполняться одновременно на разных НПВМ под управлением микрокоманд, принадлежащих указанным подпрограммам, т. е.:
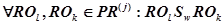 . (21)
. (21)
Справедливо утверждение о том, что отношение структуры обработки 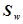 есть отношение эквивалентности. Тогда задача разбиения программы на множество подпрограмм преобразуется в задачу рационального последовательного объединения сегментов
есть отношение эквивалентности. Тогда задача разбиения программы на множество подпрограмм преобразуется в задачу рационального последовательного объединения сегментов 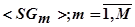 в множество подпрограмм
в множество подпрограмм 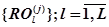 :
:
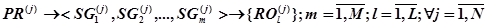 (22)
(22)
То есть, задача разбиения заключается в нахождении значения 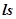 выражения (22) для всех подпрограмм
выражения (22) для всех подпрограмм 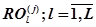 , где число подпрограмм равно числу НПВМ
, где число подпрограмм равно числу НПВМ 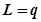 :
:
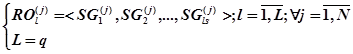 (23)
(23)
Пусть число команд 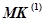 в программе
в программе 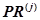 , определяемой как (18) равно
, определяемой как (18) равно 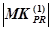 , число команд некоторого сегмента
, число команд некоторого сегмента 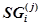 равно
равно 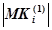 .
.
Цель разбиения программы на подпрограммы состоит в достижении одинакового времени обработки для всех этапов, то есть, в данном случае, в достижении одинакового количества команд 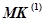 для всех подпрограмм. Тогда необходимо определить среднее число
для всех подпрограмм. Тогда необходимо определить среднее число 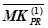 команд
команд 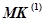 в подпрограмме:
в подпрограмме:
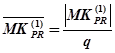 . (24)
. (24)
Далее, добавление нового сегмента 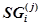 к подпрограмме возможно лишь тогда, когда разность значения
к подпрограмме возможно лишь тогда, когда разность значения 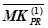 и суммарного количества команд
и суммарного количества команд 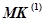 уже добавленных в подпрограмму
уже добавленных в подпрограмму 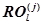 сегментов больше, чем
сегментов больше, чем 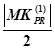 .
.
То есть, если верно условие 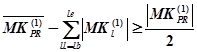 , (25)
, (25)
где 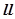 определяет номера сегментов, уже включенных в подпрограмму:
определяет номера сегментов, уже включенных в подпрограмму:
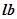 — номер первого сегмента в подпрограмме
— номер первого сегмента в подпрограмме 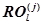 ;
;
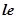 — номер последнего сегмента в подпрограмме
— номер последнего сегмента в подпрограмме 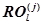 .
.
Тогда 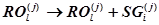 ;
; 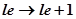 (26)
(26)
Если условие (25) неверно, то
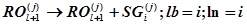 (27)
(27)
Таким образом, в соответствии с выражениями (23)-(27), нейромикропрограмма 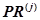 может быть рационально разделена на подпрограммы
может быть рационально разделена на подпрограммы 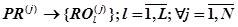 , для которых верно отношение структуры обработки информации
, для которых верно отношение структуры обработки информации 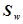 .
.
Литература:
1. Галушкин А. И. Нейронные ЭВМ — перспективное направление развития вычислительной техники — М.: Препринт, 1991.-615 с.
2. Головкин Б. А. Вычислительные системы с большим числом процессоров. М.: Радио и связь, 1995. — 320 с.
3. Злобин В. К., Григоренко Д. В., Ручкин В. Н., Романчук В. А. Кластеризация и восстанавливаемость нейропроцессорных систем обработки данных // Известия тульского государственного университета. Технические науки. — Тула: Издательство ТулГУ, 2013. — Вып.9. — Ч.2. — С.125–135.
4. Романчук В. А., Ручкин В. Н. Разработка программных средств анализа нейропроцессорных систем // Вестник РГРТУ. — Рязань: РГРТУ, 2010. — № 2. — Вып.32. — С.61–67.
5. Романчук В. А., Ручкин В. Н. Разработка программного комплекса для моделирования и анализа нейропроцессорных систем обработки изображений // Цифровая обработка сигналов. — Рязань: Информационные технологии, 2010. — № 1. — С.53–58.
6. Романчук В. А., Ручкин В. Н. Оценка результатов моделирования вычислительных систем на базе нейропроцессоров // Известия тульского государственного университета. Технические науки. — Тула: Издательство ТулГУ, 2013. — Вып.9–2 — С.194–203.
7. Романчук В. А. Моделирование нейропроцессорных систем // Отраслевые аспекты технических наук: научно-практический журнал. — Москва: ИНГН, 2013. — № 10(34). — С.19–24.
8. Романчук В. А., Ручкин В. Н. Разработка алгоритмов определения вида структуры нейропроцессорной системы на основе описания связей ее элементов // Информатика и прикладная математика: межвуз. сб. науч. тр. — Рязань: РГУ имени С. А. Есенина, 2011. — Вып.17. — С.106–109.
9. Романчук В. А. Инновационный программный комплекс моделирования вычислительных систем на базе нейропроцессоров «НейроКС» // Современные научные исследования и инновации. — Декабрь, 2012 [Электронный ресурс]. — URL: http://web.snauka.ru/issues/2012/12/19407.
10. Романчук В. А. Разработка алгоритмов определения связей элементов вычислительной структуры на базе нейропроцессоров // Информатика и прикладная математика: межвуз. сб. науч. тр. — Рязань: РГУ имени С. А. Есенина, 2011. — Вып.17. — С.102–105.
11. Романчук В. А. Оптимизация программных и аппаратных средств сложных вычислительных систем на базе нейропроцессоров // Моделирование, оптимизация и информационные технологии. — 2015. — № 1(8) 3 [Электронный ресурс]. URL: http://moit.vivt.ru/wp-content/uploads/2015/03/Romanchuk_1_15_1.pdf.
12. Ручкин В. Н., Романчук В. А., Фулин В. А., Пролыгина А. А. Экспертная система нечеткой кластеризации нейропроцессорных систем // Известия тульского государственного университета. Технические науки. — Тула: Издательство ТулГУ, 2014. — Вып.6. — С.162–167.







