Статья посвящена разработке одного из средств предпрофильной подготовки выпускников основной школы — элективного курса по математике, спроектированного на интеграционной основе.
Ключевые слова: интеграционные связи, интродисциплинарные связи, интердисциплинарные связи, предпрофильная подготовка, элективный курс.
Одной из главных задач выпускника основной ступени общего образования является построение своей индивидуальной образовательной траектории. Выпускник 9 класса, получающий аттестат об основном общем образовании, ориентируется на получение среднего (полного) общего образования, начального или среднего профессионального образования. Многие выпускники основной школы еще не определились со своей будущей профессией и поэтому собираются продолжать обучение в старшей школе. В связи с этим актуализируется проблема выбора будущего профилирующего направления. Поэтому одним из условий такого самоопределения обучающегося является введение предпрофильной подготовки.
Предпрофильная подготовка, в частности, включает в себя элективные курсы. Как правило, это небольшие по объему (до 30 учебных часов) курсы, основная цель которых состоит в расширении и углублении знаний по предмету, расширении кругозора учащихся, развитии определенных сторон мышления и формировании ряда личностных качеств.
С введением с 2015 года двух уровней единого государственного экзамена по математике — базового и профильного — проблема проектирования элективных курсов по математике стала особенно актуальной. Выпускник 9 класса, планирующий свое дальнейшее обучение в старшей школе, должен не просто определиться с профилирующим направлением, но и выбрать для себя уровень будущего обязательного ЕГЭ по математике.
На наш взгляд, элективные курсы по математике не должны повторять темы школьной программы. Их цель состоит в удовлетворении познавательных интересов учащихся, формировании их образовательных траекторий, знакомству с математикой, как с общекультурной ценностью, компонентом общечеловеческой культуры. Основой подобных курсов должен стать интеграционный подход, что способствует формированию единых представлений о мире, картины мира как целостного процесса [5. С. 66–72].
Исходя из этого, мы считаем возможным введение таких элективных курсов по математике, как «Эйлеровы графы» [3. С.689–691], «Специальные числа натурального ряда», «Рекуррентные соотношения и числа Фибоначчи», «Диофантовы уравнения» [4. С. 1–5] и др.
Остановимся на содержании разработанного нами элективного курса «Некоторые специальные числа натурального ряда».
Понятие числа является фундаментальным понятием математики. Линия числовых систем — одна из основных содержательно методических линий школьного курса математики. Числовые системы изучаются школьниками на протяжении всех лет обучения. Но, как правило, изучение натуральных чисел заканчивается в 5–6 классах знакомством с простыми и составными числами. Специальные числа натурального ряда — пифагоровы и героновы тройки, числа Фибоначчи, Люка и Каталана, фигурные, совершенные и дружественные числа — имеют богатую историю, различные практические приложения, интересные и разнообразные свойства.
Так, например, изучение совершенных и дружественных чисел не требует специальных знаний, выходящих за пределы программы основной школы, но позволяет реализовать целый ряд разнообразных интеграционных связей, как интродисциплинарных (с различными разделами математики), так и интердисциплинарных (с историей, культурой, искусством).
Греческие математики называли число совершенным, если сумма всех его собственных делителей (т. е. натуральных делителей, отличных от самого числа) была равна этому числу.
Им были известны четыре таких числа: 6 (=1+2+3), 28 (=1+2+4+7), 496 (=1+2+4+8+16+31+62+124+248) и 8128 (=1+2+4+8+16+32+64+127+254+508+1016+ +2032+4064).
Первые два числа знали уже пифагорейцы (VI в. до н. э.), которые считали, что они отражают совершенство, а заслуга открытия двух последних принадлежит Евклиду. Эти числа приведены в Арифметике Никомаха Геразского. Евклид доказал, что если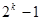 
, где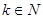 
— простое число, то и 
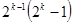— число совершенное. В 1849 г. Эйлер доказал, что все четные совершенные числа имеют именно такой вид [1. С.118].
Поскольку число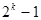 
может быть простым только при простом k, то первые четыре совершенные числа получаются при:
k=2 (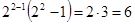
),
k=3 (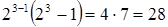
),
k=5 (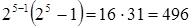
),
k=7 (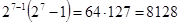
).
Пятое совершенное число обнаружил немецкий математик Региомонтан (1436–1476) лишь в XV веке. Это число также подчиняется условию Евклида. Она равно 33 550 336 и соответствует k=13 в формуле Евклида [2. С.14].
Впоследствии были найдены еще 14 совершенных чисел, причем последние 7 были найдены с помощью компьютеров. Существует гипотеза о бесконечности множества четных совершенных чисел. Что касается нечетных совершенных чисел, то пока не найдено ни одного такого числа, но, в то же время не доказано, что таких чисел не существует.
Числа, сумма собственных делителей которых была больше или меньше самого числа, назывались греческими авторами соответственно избыточными и недостаточными. Эта терминология сохранилась и в наше время.
Совершенные числа обладают интересными свойствами, в частности,
- последняя цифра четного совершенного числа всегда равна 6 или 8,
- каждое четное совершенное число является треугольным, т. е. является суммой первых натуральных чисел,
- число натуральных делителей четного совершенного числа четно,
- четное совершенное число (кроме 6) сравнимо с 1 по модулю 9
и многими другими. Доказательство этих свойств доступно школьникам и рассматривается в рамках элективного курса.
Дружественные числа — это два натуральных числа, каждое из которых равно сумме собственных делителей второго числа (заметим, что каждое совершенное число можно рассматривать как дружественное самому себе).
Открытие наименьшей пары дружественных чисел (220, 284) (220=1+2+4+71+142, 284=1+2+4+5+10+11+20+22+44+55+110) приписывают пифагорейцам. Первым из сохранившихся документов, содержащих упоминание о дружественных числах, является трактат «Изложение пифагорейского учения», написанный в III в. н. э. Ямвлихом из Хальциса. Ямвлих рассказывает, как однажды великий Пифагор на вопрос, кого следует считать другом, ответил: «Того, кто является моим вторым я, как числа 220 и 284» [1. С.134]. В течение пятнадцати веков эта пара оставалась единственной! Нахождение общего способа получения дружественных чисел до сих пор является нерешенной задачей. Дружественные числа также имеют интересные свойства, причем некоторые из них вполне доступны для старшеклассников.
Изучение специальных чисел натурального ряда повышает интерес школьников к теории чисел, что впоследствии дает возможность рассмотреть задачи олимпиадного типа, встречающихся в задачах типа 21 Единого Государственного Экзамена по математике Российской Федерации профильного уровня (до 2015 г. — задача типа С6). Тем самым реализуются интродисциплинарные (внутриматематические) связи элективного курса между элементарной математикой и теорией чисел.
Богатая и драматичная история открытия совершенных и дружественных чисел и их свойств позволяет осуществить интердисциплинарные связи математики с историей, искусством и литературой, поэтому данный элективный курс будет полезен и тем учащимся, которые не планируют для себя в дальнейшем углубленное изучение математики.
Таким образом, элективный курс «Некоторые специальные числа натурального ряда», построенный на интеграционной основе, позволяет не только пробудить и развить интерес обучающихся к математике, но и повысить уровень их общей культуры.
Литература:
1. Деза Е. И. Специальные числа натурального ряда: учеб. пособие. — М.: Книжный дом «ЛИБРОКОМ», 2010.
2. Депман И. Совершенные числа // Квант. — 1991. — № 5. — С. 13–17, 22
3. Жмурова И. Ю., Коршунова Л. А. Элективный курс «Эйлеровы графы» как средство реализации интеграционных связей математики // Молодой ученый. — 2013. — № 5. — С.689–691
4. Жмурова И. Ю., Ленивова А. В. Диофантовы уравнения от древности до наших дней // Молодой ученый. 2014. № 9. С. 1–5
5. Полякова Т. С., Жмурова И. Ю., Лялина Е. В. Интеграционные связи и их оценка учителями математики и бакалаврами педагогико-математического образования // Методический поиск: проблемы и решения. 2015. № 1 (18). С. 66–72.
