В статье рассматриваются различные численные методы решения задачи непоршневого вытеснения нефти водой. Произведен анализ результатов расчетов для двумерной фильтрации.
Ключевые слова: двухфазнаяфильтрация, модель Баклея — Леверетта, модифицированный попеременно-треугольный метод.
Для рационального освоения нефтяных месторождений большое значение имеют знание современных гидродинамических методов получения информации и научных основ установления оптимального режима эксплуатации скважин. Создано множество методов и алгоритмов изучения процесса фильтрации, т. е. процесса протекания жидкостей в среде [1]. Статья посвящена исследованию различных численных методов решения задачи фильтрации и разработке достаточно точных и эффективных вычислительных алгоритмов.
Постановка задачи и разностная схема. Рассмотрим классическую модель двухфазной фильтрации Баклея-Леверетта [1], которая наиболее точно описывает задачу нефтедобычи с помощью дифференциальных уравнений гидродинамики [2]:
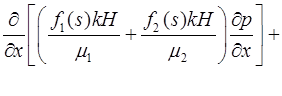
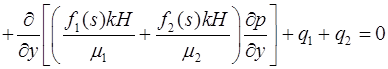, (1)
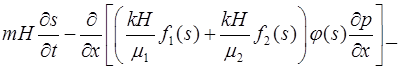
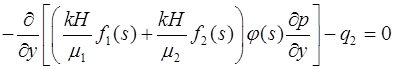, (2)
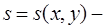водонасыщенность; 
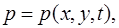давление;
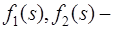относительные фазовые проницаемости для нефти и воды соответственно; 
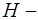мощность пласта; 
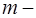пористость пласта; 
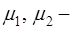вязкость нефти и воды соответственно; 
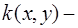проницаемость пласта; 
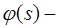функция Баклея―Леверетта
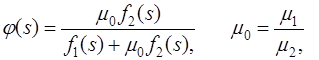(3)
для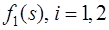 
будем использовать полиномы второго порядка
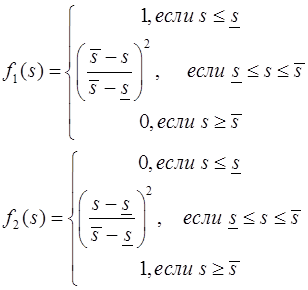, (4)
где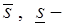 
предельные значения водонасыщенности [2].
В области G с границей Г рассмотрим граничные условия. Если граница непроницаемая то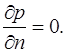 
Если граница проницаемая, рассмотрим граничные условия 1 и 2 рода:
при совместном движении фаз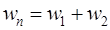 
, где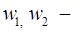 
потоки нефти и воды, удовлетворяющие условиям:
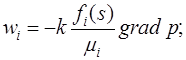
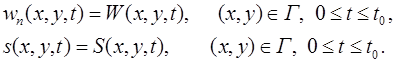
При заданном отборе или давлении
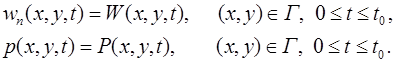
Для суммарного потока, вытекающего через границу, граничное условие для насыщенности имеет вид
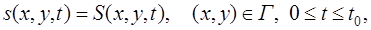где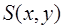 
водонасыщенность на границе области в данный момент времени.
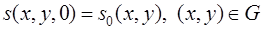- начальное условие. (5)
Итак, для уравнений (1), (2) построена задача Коши (1)-(5).
Решение задачи (1)-(5) будем искать в прямоугольной области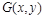 
. В области построим равномерную пространственную сетку
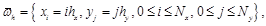
неравномерную временную сетку
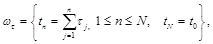
где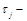 
величина временного шага, определяемая из условий устойчивости и пространственно-временную сетку 
.
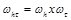Получим консервативную разностную схему интегро-интерполяционным методом [7,8,10].
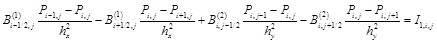(6)
где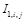 
— функция принимает значение 0, если узел сетки 
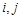расположен вне скважины, 
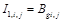, в случае если узел расположен на скважине
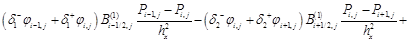
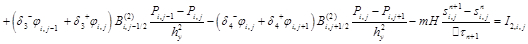, (7)
где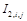 
— функция принимает значение 0, если узел сетки 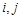расположен вне скважины, 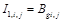, в случае если узел расположен на нагнетательной скважине, то 
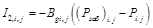,а в случае эксплуатационной скважины:
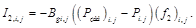
Символы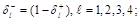 
определяются из условий [9]:
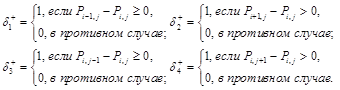(8)
Коэффициенты уравнения (6) и (7) получим, используя интегро-интерполяционный метод:
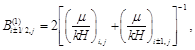
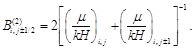(9)
Численная реализация задачи. При численной реализации разностной задачи основной объем вычислительной работы приходится на решение системы (6). Если перейти к более подробным пространственным сеткам вычислительные затраты для нахождения давления растут и превышают 90 % для последовательных алгоритмов решения задачи. Применим усовершенствованный модифицированный попеременно-треугольный метод, имеющий высокую скорость сходимости в случае сильно неоднородных пластов и применения подробных пространственных сеток [3,5,6].
Представим систему (6) в стандартном виде:
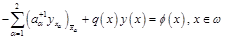(10)
, 
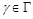, (11)
, 
, 
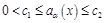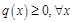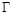— граница прямоугольника 
, 
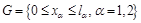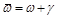— равномерная сетка, 
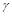— множество граничных узлов сетки.
Коэффициентами уравнений (10) и (6) связаны равенством:
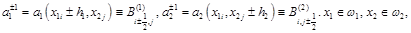
где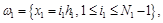 
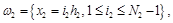
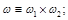
сетка ω — равномерная, покрывающая область G.
Сеточные функции в равенствах (6) и (10) задаются следующим образом
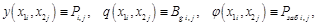
Рассмотрим смещенные сетки
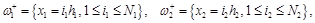
Запишем сеточную задачу (11), в операторном виде [7]:
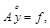
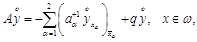(12)
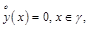
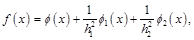
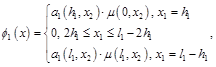
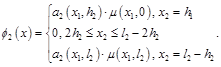
Схема итерационного двухслойного модифицированного попеременно-треугольного метода имеет вид [3,4,5]:
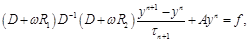(13)
где 
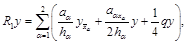
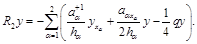(14)
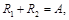
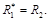Оценки для постоянных Δ и δ, входящих в неравенства:
, 
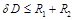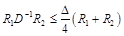. (15)
имеют следующий вид
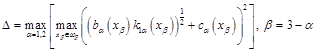, δ =1, (16)
где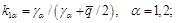 
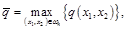(17)
,
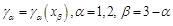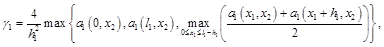
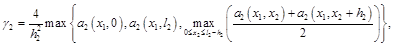
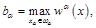
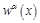— решение краевой задачи:
, 
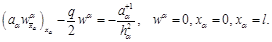
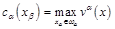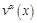— решение краевой задачи:
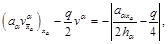
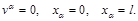(18)
Выражение для функции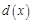 
, имеет вид
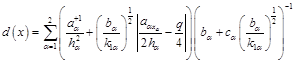(19)
Поскольку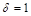 
, то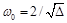 
и при использовании чебышевского ускорения [8] для числа итераций справедлива оценка: 
, 
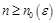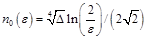. Аналогично «стандартному» варианту МПТМ отсюда имеем оценку 
.
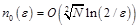Заключение. Численные эксперименты показали заметное уменьшение числа итераций по сравнению со «стандартным» алгоритмом модифицированного попеременно-треугольного метода, за счет учета функции источников [3].
Литература:
1. Коновалов А. Н. Задачи фильтрации многофазной несжимаемой жидкости. — Новосибирск: Наука, 1988. — 166 с.
2. Коновалов А. Н. Метод скорейшего спуска с адаптивным попеременно-треугольным переобусловливателем // Дифференциальные уравнения. —2004.—Т. 40, № 7. — С. 953–963.
3. Коновалов А. Н. К теории попеременно-треугольного итерационного метода // Сибирский математический журнал. —2002. —Т. 43, № 3. — С. 552–572.
4. Сухинов А. И. Модифицированный попеременно-треугольный метод для задач теплопроводности и фильтрации // Вычислительные системы и алгоритмы. — 1984. — С.52–59.
5. Сухинов А. И., Чистяков А. Е. Адаптивный попеременно-треугольный метод для решения сеточных уравнений с несамосопряженным оператором // Математическое моделирование. —2012. —Т. 24, № 1. — С. 3–20.
6. Сухинов А. И., Шишеня А. В. Повышение эффективности попеременно-треугольного метода на основе уточненных спектральных оценок // Математическое моделирование. —2012. —Т.24, № 11. — С. 10–22.
7. Самарский А. А. Теория разностных схем. М.: Наука, 1989. —656 с.
8. Самарский А. А., Николаев Е. С. Методы решения сеточных уравнений. М.: Наука, 1978. —592 с.
9. Григорян Л. А. Моделирование фильтрации двухфазной жидкости методом конечных элементов. Вестник. Северо-Кавказский федеральный университет. Ставрополь: СКФУ,-2013. -№ 2-С.13–16.
10. Григорян Л. А. Математическое моделирование задачи разработки нефтяных месторождений. / Л. А. Григорян, Е. Ф. Тимофеева // Естественные и математические науки в современном мире / Сборник статей по материалам ХVIII международной научно-практической конференции. Новосибирск: Изд. «СибАК», 2014. 218 с.
