В настоящее время при моделировании различных объектов широко используются такие направления науки, как нейронные сети, генетические алгоритмы и нечеткие системы — так называемые современные вычислительные технологии. В данной работе рассмотрим прикладные возможности одного из этих направлений — нейронные сети. Искусственные нейронные сети строятся на основе знаний о функционировании нервной системы живых организмов. То есть сетевые конфигурации и алгоритмы строятся как аналоги процессов, происходящих в живых нервных системах. При этом ученным часто приходится выходить за приделы современных знаний биологии в поисках структур, которые смогут выполнять нужные и важные функции задаваемой информационной системой на должном уровне [2,4,9]. Поэтому иногда приходится отказываться от свойства правдоподобия, но даже при таком подходе состоят из элементов которые аналогичны большинству элементарных функций биологического нейрона (они могут организоваться по способу нашего мозга, или не могут, это выбирают создатели). Хотя нейронные сети и похоже на наш мозг (хотя скорей это только внешнее подобие), но они демонстрируют удивительное число свойств присущих нашему мозгу [1,3]. Например, нейронные сети могу обучатся за счет поступления информации, обучатся на случаях, которые уже происходили в них. В нейронных сетях можно выделить несколько плюсов, которых нету в других системах [7,8,5].
1. Обучение — то есть нейронные сети могут менять своё поведение в зависимости от условий внешней среды. После предъявления входных сигналов, нейронные сети самонастраиваются, чтобы обеспечить необходимую реакцию. В настоящий момент разработано множество обучающих алгоритмов.
2. Обобщение — то есть сеть может пренебрегать небольшими изменениями входных сигналов. Эта способность позволяет видеть сквозь искажения информации. Она необходима для распознавания образов в реальном мире. Так же она помогает преодолеть требование к строгой точности, которая так необходима простым компьютерам. Важно отметить, что нейронная сеть делает обобщение сама, а не с помощью программ, так называемого «человеческого интелекта».
3. Абстрагирование — позволяет извлекать сущность из входных сигналов, и создавать что-то новое. Например, в сигнале искажена буква «Т», так после определенного обучения, нейронная сеть породит букву совершенной формы, то есть она научится создавать то, что никогда не видела.
4. Применимость — нейронная сеть не годится для выполнения «мелких задач», но им будут отдавать предпочтения в большом классе задач по распознаванию образов, с которыми плохо справляются обычные компьютеры.
Рассмотрим нейрон с точки зрения биологии человека. Нервная система человека, построенная из элементов, называемых нейронами, имеет очень большую сложность. Приблизительно 1011 нейронов участвуют в 1015 связях [4,9]. Каждый нейрон обладает огромным количеством функций, свойств, а также качествами, общими с другими элементами тела, но его уникальным свойством можно считать прием, обработку и передачу информации по нервным путям.
Искусственный нейрон имитирует приближенную копию биологического нейрона. На вход искусственного нейрона поступает сигнал, который является выходом другого нейрона. Искусственные нейронные сети можно разделить на два вида: однослойные и многослойные искусственные нейронные сети [5,6]. Бывает самое разнообразное количество нейронных сетей, но большинство из них подчиняется одной конфигурации. Входной сигнал умножается на вес ребра, по которому идет, и поступает в суммирующий блок.
Однослойная нейронная сеть представляет собой сеть из определенной группы нейронов. Сеть состоит из определенных точек, которые помогают в распределении сигналов, а также с вычислительными нейронами, которые считаются слоем (то есть распределители не считаются слоем, скорей они помогают в создании сети и распределении ресурсов сети). Любая нейронная сеть может быть представлена в виде графа. (рисунок 1)
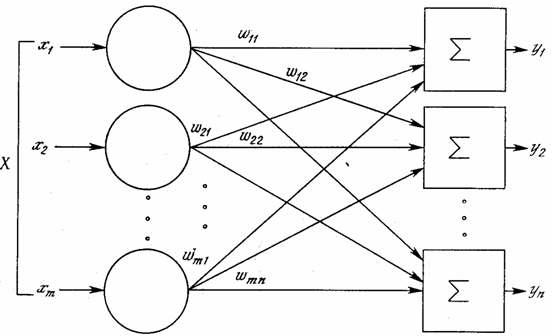
Рис. 1. Однослойная нейронная сеть
Вычислительные нейроны на рисунке 1 представлены в виде квадратов, когда распределительные элементы имеют вид кружков. В данном примере каждая точка распределения имеет связь с каждым вычислительным нейроном. Можно сказать, что данный пример является эталонным, так как обычно не все распределительные точки имеют связь с каждым вычислительным нейроном. В жизни нейронные сети представляют собой не полный граф, то есть некоторые связи могут отсутствовать. Каждое ребро записывается двумя значениями: m — номером вычислительного нейрона и n — номером выхода. То есть вычислительная мощность считается по матрице.
Многослойная искусственная нейронная сеть представляет собой более сложную структуру, которая обладает более высокой вычислительной мощью и вычислительными возможностями. Многослойные нейронные сети построены из определенных отделов мозга. Многослойные нейронные сети могут создаваться с помощью нескольких слоев, то есть выход из одного слоя является входом для следующего. (рисунок 2)
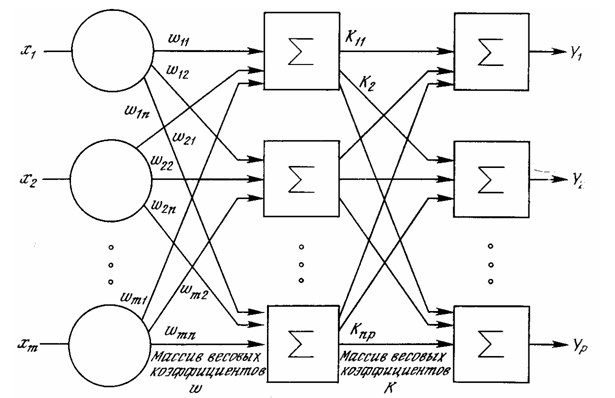 Рис. 2. Многослойная нейронная сеть
Рис. 2. Многослойная нейронная сеть
На рисунке 2 представлена многослойная нейронная сеть эталонного вида, то есть со всеми связями.
Как уже ранее говорилось, любая нейронная сеть может обучаться, но делает это она с помощью специализированных программ. Сейчас для обучения нейронной сети нужно решит огромное количество различных проблем, чтобы узнать на правильном пути мы находимся или нет, но уже есть так называемая «говорящая сеть» Сейновского, которая позволяет решить большинство из этих проблем [5,7,8,9].
Целью обучения является научить нейронную сеть выдавать необходимое количества выходов при некотором множестве входов. Сейчас существует два подхода обучения нейронных сетей: первый представляет собой обучение без учителя, второй с учителем. Обучение с учителем предполагает, что для каждого входного вектора существует целевой вектор, который направляется на необходимый выход. Вместе они называются обучающей парой. Нейронная сеть обучается на нескольких таких парах, а не на одной. В основном обучение происходит по одной стандартной схеме. Выходной вектор проходит по сети, вычисляется выход сети и сравнивается со значением выходного вектора обучающего вектора, разность с помощью обратной связи возвращается в сеть и вес ребер меняется в соответствии с алгоритмом, который стремится минимизировать ошибку [2,5,7,9]. Каждый обучающий вектор используется последовательно, после чего вычисляется разность и веса подстраиваются для каждого вектора, пока разность по массиву не достигнет низкого уровня. Обучение с учителем часто критикуют за биологическую неправдоподобие.
В свою очередь обучение без учителя является более правдивой моделью обучения. Она была развита Кохоненом [7,8,9]. В обучении без учителя нет сравнения выходных данных с идеальными выходными данными, которые заложены в системе обучения. В обучении используются только входные данные, то есть обучающие алгоритмы подстраивают веса сети так, чтобы входные и выходные вектора были близки. Обучающая программа с помощью статистических методов группирует векторы в классы. То есть входной вектор из определенного класса даст определенный векторный выход. До обучения нельзя предсказать какой выход будет у определенного входного вектора, но после трансформации нейронной сети в определенную форму, которая создается процессом обучения, это перестало быть недостатком этого метода, а идентифицировать связь между входом и выходом обычно не составляет труда.
Большинство алгоритмов обучения произошло из концепции Хебба [3,5,7,9]. Им была предложена модель обучения без учителя, в которой все ребра возрастают, если источник и приемник активированы. То есть часто используемые пути в сети усиливаются через повторения пути.
Свой метод, или точнее было сказать гипотезу (потому что изначально его метод обучения являлся гипотезой), Хебб выдвинул на основе физических и психологических исследований, которая говорит свою о том, как обучается набор биологических нейронов [3,6,9]. Его теория имела только локальное взаимодействие между нейронами. Предполагалось, что обучения будет неконтролируемым (отсутствие глобального учителя). Хотя его гипотеза не имеет математического анализа, она получила статус универсальных допущений. Нейронные сети, использующие обучение по Хеббу, развивались на протяжении долгого времени, но сейчас уже создаются более действующие(эффективные) методы обучения, такие как метод обучения Уидроу-Хоффа, самоорганизация, обучение персептрона.
Обучение персептрона [1,4,8]. Данную модель разработал Разенблатт в 1957 году. Она вызвала огромный интерес у исследователей. Обучение персептрона представляет собой классический способ обучения с учителем, то есть на множестве входов генерируются значения, которые не превышают 0 и 1, и алгоритм вырабатывает путь обучения. После обучения сеть получает на входе набор непрерывных входов и вырабатывает требуемый выход в виде вектора.
Метод обучения Уидроу-Хоффа [2,5,9]. Этот метод обучения строится на алгоритме обучения персептрона, действует также, как метод персептрона, с одним изменением. В данном методе используются непрерывные сигналы, вместо бинарных. То есть, если в предыдущем методе обучения ошибки вычислялись бинарными сигналами, то в этом методе они непрерывные.
Самоорганизация, или алгоритмы Кохонена строятся на исследованиях самоорганизующихся структурах, которые используются для распознавания личности [3,6]. Алгоритмы Кохонена основываются на методе обучения без учителя. После обучения подача входного вектора из определенного класса будет приводить к возбуждению уровня в каждом выходном нейроне. Такой метод обучения проводится без вектора, то есть определить к какому классу нейрон будет относиться заранее невозможно. Перед обучением каждый компонент вектора получает случайную величину, а затем каждый вектор нормализуется в вектор с единичной длиной.
Литература:
1. Барский А. Б. Нейронные сети: распознавание, управление, принятие решений. — М.: Финансы и статистика, 2004. — 176 с.
2. Осовский С. Нейронные сети для обработки информации / Пер. с польского И. Д. Рудинского. — М.:Финансы и статистика, 2002. — 344с.
3. Каллан Роберт. Основные концепции нейронных сетей: Пер. с англ. — М.: Издательский дом «Вильямс», 2001
4. Комарцова Л. Г., Максимов А. В. Нейрокомпьютеры: Учеб. пособие для вузов. — 2-е изд.,перераб. и доп. — М.: Изд-во МГТУ им. Н. Э. Баумана, 2004. — 400с.
5. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польск. И. Д. Рудинского- М.: Горячая линия-Телеком, 2006–452с.
6. Kureychik V. V. Melikhova O. A. Gaydukov A. B. Chumichev V. S. Dzhambinov S. V. Bukach S. A. Proceedings of the International Scientific and Practical Conference «Innovative technologies in science, Vol. I (February 21–22, 2015, Dubai, UAE)". — Dubai.: Rost Publishing, 2015. — P. 57–67.
7. Мелихова О. А., Чумичев В. С., Джамбинов С. В., Гайдуков А. Б. Некоторые аспекты криптографического взлома и повышения надежности алгоритмов шифрования// Молодой ученный.- Казань, № 11(91), 2015. — С. 392–394
8. Мелихова О. А. Приложение матлогики к проблемам моделирования// Известия ЮФУ. Технические науки. — Таганрог: Изд-во ТТИ ЮФУ, 2014. № 7(156). — С.204–214.
9. Уоссермен Ф. Нейрокомпьютерная техника: Теория и практика. М.:Мир,1992- 184с.







