Данная работа является продолжением работ [1]…[4], где подробно, без сокращений дан математический аппарат асинхронного двигателя (АД). В этой работе расчет параметров двигателя производится в Script, а моделирование идет в Simulink. Эта работа важна для учебных целей для студентов.
В работах [2], [3], [4] были получены следующие уравнения с переменными 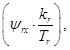
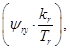
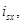
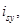
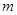 и
и 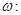
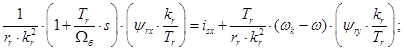 (1)
(1)
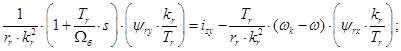 (2)
(2)
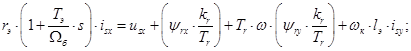 (3)
(3)
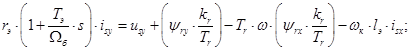 (4)
(4)
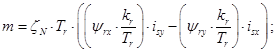 (5)
(5)
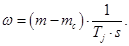 (6)
(6)
В работах [1]…[4] приведены формулы для расчета всех коэффициентов, входящих в уравнения (1)…(6). Приведем некоторые из них:
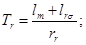
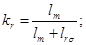
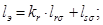
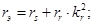
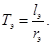
Рассмотрим два варианта.
Вариант 1. Математическая модель АД с переменными 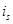 —
— 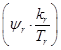 на выходе апериодических звеньев.
на выходе апериодических звеньев.
Из уравнений (1) - (4) получим следующие уравнения:
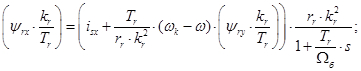
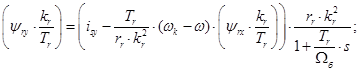
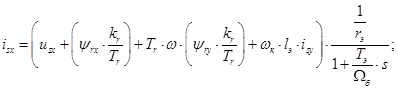
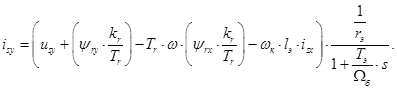
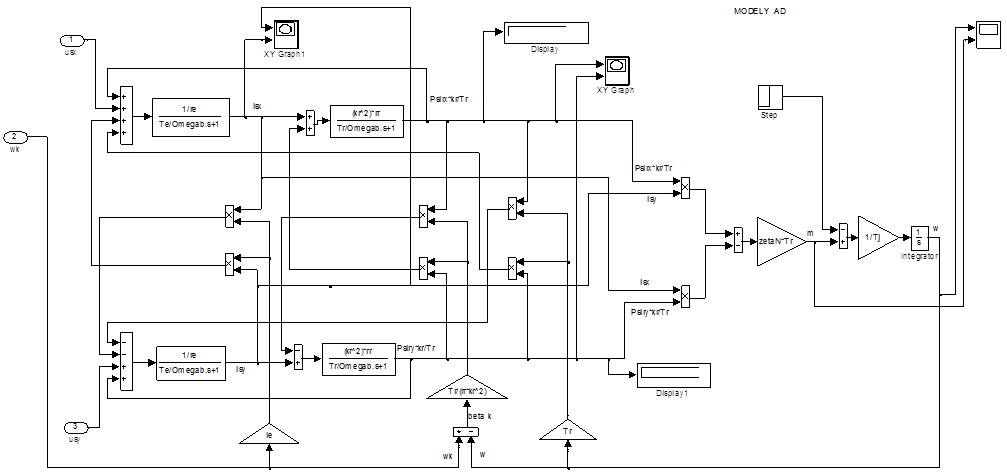
Уравнения (5) и (6) остаются без изменения. Этим уравнениям соответствует следующая полная структурная схема (рис. 1).
Вариант 2. Математическая модель АД с переменными 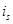 —
— 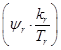 на выходе интегрирующих звеньев.
на выходе интегрирующих звеньев.
Из уравнений (1)…(4) получим следующие уравнения:
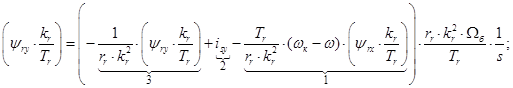
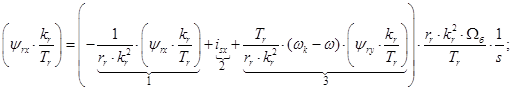
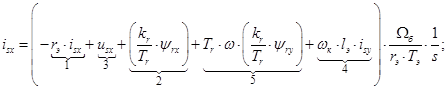
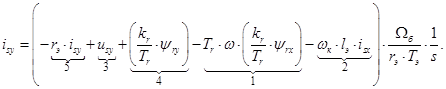
Уравнения (5) и (6) остаются без изменений.
Этим уравнениям соответствует полная структурная схема, представленная на
рис. 2.
В работе [6] в главе 6 «Примеры» дан образец расчета параметров асинхронного двигателя. В наших дальнейших работах направленных на подготовку студентов к исследовательской работе, глава 6 окажет неоценимую помощь. Можно было бы по аналогии рассмотреть паспортные данные любого другого двигателя, но для проверки правильности выводов уравнений сделанных исследовательской группой самостоятельно, необходимо постоянно выходить на многие полученные результаты в работе [7]. Поэтому, этот пример расчета окажется очень полезным.
Номинальные данные:
Номинальный режим работы S1;
Номинальная мощность 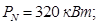
Номинальное фазное напряжение 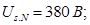
Номинальный фазный ток 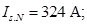
Номинальная частота 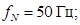
Номинальная синхронная скорость 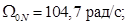
Номинальная скорость ротора 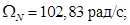
Номинальный КПД 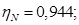
Номинальный коэффициент мощности 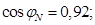
Число пар полюсов 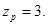

Рис. 2. Математическая модель АД с переменными 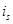 —
— 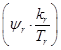 на выходе интегрирующих звеньев
на выходе интегрирующих звеньев
Параметры Т-образной схемы замещения при номинальной частоте:
Активное сопротивление обмотки статора 
Индуктивное сопротивление рассеяния обмотки статора 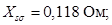
Активное сопротивление обмотки ротора, приведенное к статору 
Индуктивное сопротивление рассеяния обмотки ротора, приведенное статору 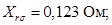
Главное индуктивное сопротивление 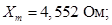
Суммарный момент инерции двигателя и механизма 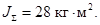
Базисные величины системы относительных единиц:
Напряжение 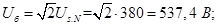
Ток 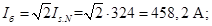
Частота 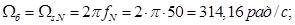
Скорость ротора 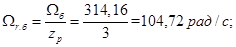
Сопротивление 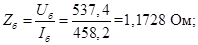
Потокосцепление 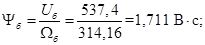
Индуктивность 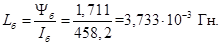
Используя номинальные данные двигателя, определяем:
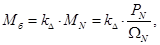
где 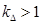 – коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (
– коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (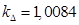 ).
).
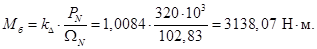
В качестве базисной мощности выбираем значение электромагнитной мощности двигателя в номинальном режиме, определяемое по следующей формуле:
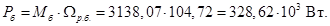
Относительные значения параметров схемы замещения двигателя:
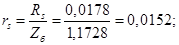
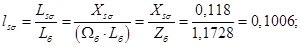
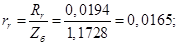
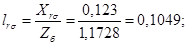
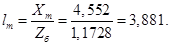
Механическая постоянная времени:
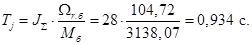
Номинальное значение скольжения:
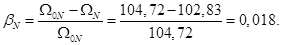
Относительное значение номинальной скорости ротора:
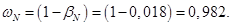
Нормирующий энергетический коэффициент:
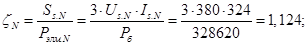
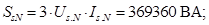
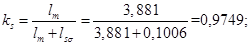
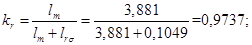
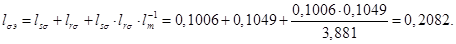
При расчете режимов работы, для того чтобы 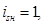
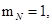
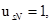
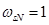 и
и 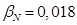 необходимо откорректировать
необходимо откорректировать 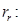
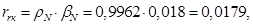
где 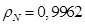 – корректирующий коэффициент [6, с. 296].
– корректирующий коэффициент [6, с. 296].
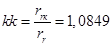 - коэффициент, показывающий отношение
- коэффициент, показывающий отношение 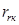 к
к 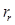 .
.
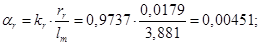
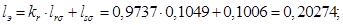
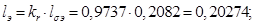
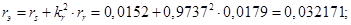
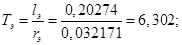
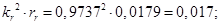
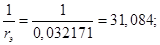
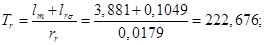

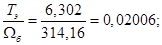
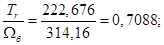
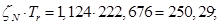
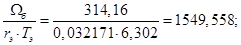
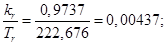
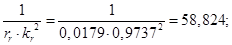
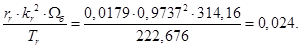
Расчет этих коэффициентов производим в Script:
%Номинальные данные
PN=320000;
UsN=380;
IsN=324;
fN=50;
Omega0N=104.7;
OmegaN=102.83;
nN=0.944;
cos_phiN=0.92;
zp=3;
%Параметры Т-образной схемы замещения при номинальной частоте
Rs=0.0178;
Xs=0.118;
Rr=0.0194;
Xr=0.123;
Xm=4.552;
J=28;
%Базисные величины системы относительных единиц
Ub=sqrt(2)*UsN;
Ib=sqrt(2)*IsN;
OmegasN=2*pi*fN;
Omegab=OmegasN;
Omegarb=Omegab/zp;
Zb=Ub/Ib;
Psib=Ub/Omegab;
Lb=Psib/Ib;
kd=1.0084;
Mb=kd*PN/OmegaN;
Pb=Mb*Omegarb;
rs=Rs/Zb;
ls=Xs/Zb;
rr=Rr/Zb;
lr=Xr/Zb;
lm=Xm/Zb;
Tj=J*Omegarb/Mb;
betaN=(Omega0N-OmegaN)/Omega0N;
wN=(1-betaN);
SsN=3*UsN*IsN;
zetaN=SsN/Pb;
ks=lm/(lm+ls);
kr=lm/(lm+lr);
lbe=ls+lr+ls*lr*lm^(-1);
roN=0.9962;
rrk=roN*betaN;
alphar=kr*rr/lm;
le=kr*lbe;
re=rs+(kr^2)*rr;
Te=le/re;
Tr=(lm+lr)/rr;
Преобразователь координат и блок ориентации подробно приведены в работах [3] и [4] и остаются без изменений.
Общий вид системы для двух вариантов приведен на рис. 3.
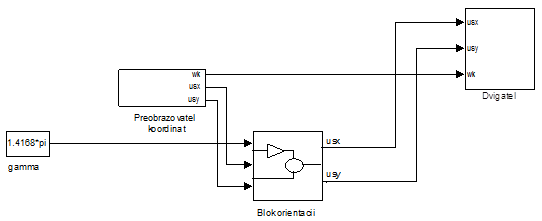
Рис. 3. Общий вид системы с двигателем двух вариантов (с интегрирующими и апериодическими звеньями)
Алгоритм пуска системы Script-Simulink заключается в следующем: открываем набранные параметры двигателя в Script → запускаем Run → открываем модель системы и производим пуск.
Результаты для двух вариантов одинаковы и приведены на рис. 4, 5 и 6.
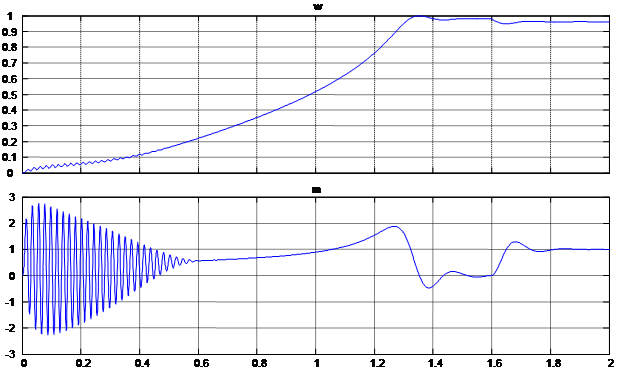
Рис. 4. Графики скорости и момента
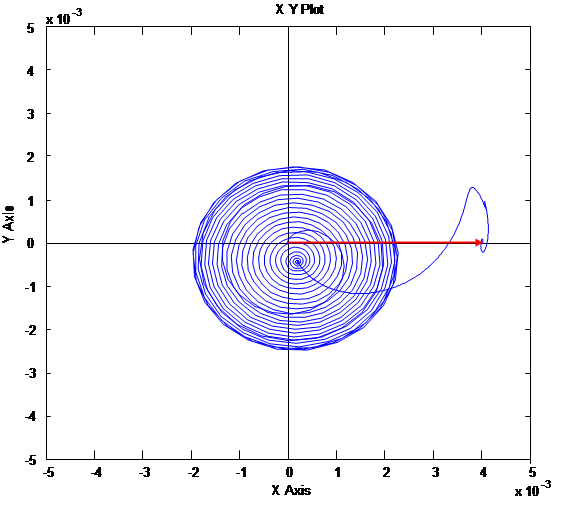
Рис. 5. Ориентация системы координат по потокосцеплению ротора
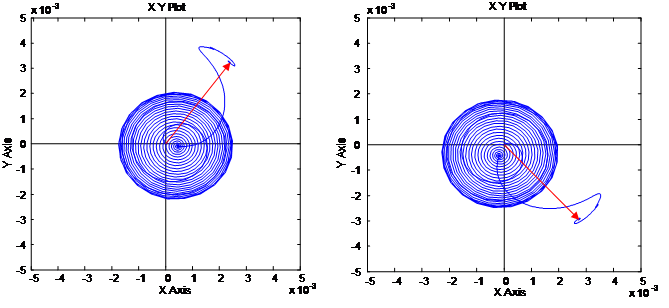
Рис. 6. Произвольная ориентация системы координат
Литература:
1. Емельянов А.А., Козлов А.М., Бесклеткин В.В., Авдеев А.С., Чернов М.В., Киряков Г.А., Габзалилов Э.Ф., Фуртиков К.А., Реутов А.Я., Королёв О.А. Математическая модель асинхронного двигателя с переменными 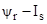 в произвольной системе координат // Молодой ученый. – 2015. - № 13. – С. 7-20.
в произвольной системе координат // Молодой ученый. – 2015. - № 13. – С. 7-20.
2. Емельянов А.А., Козлов А.М., Бесклеткин В.В., Авдеев А.С., Чернов М.В., Киряков Г.А., Габзалилов Э.Ф., Фуртиков К.А., Реутов А.Я., Королёв О.А. Пространственные векторы в асинхронном двигателе в относительной системе единиц // Молодой ученый. - 2015. - № 11. - С. 133-156.
4. Емельянов А.А., Бесклеткин В.В., Авдеев А.С., Чернов М.В., Киряков Г.А., Габзалилов Э.Ф., Фуртиков К.А., Реутов А.Я., Королёв О.А. Математическая модель асинхронного двигателя с переменными 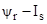 в произвольной системе координат на основе интегрирующих звеньев // Молодой ученый. — 2015. — № 15 (95). — С. 7-30.
в произвольной системе координат на основе интегрирующих звеньев // Молодой ученый. — 2015. — № 15 (95). — С. 7-30.
5. Медведев А.В., Емельянов А.А., Клишин А.В. Математическая модель асинхронного двигателя в неподвижной системе координат с переменными ir – ψr // Молодой ученый. — 2010. — №4. — С. 8-24.
6. Шрейнер Р.Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р.Т. Шрейнер, А.В. Костылев, В.К. Кривовяз, С.И. Шилин. Под ред. проф. д.т.н. Р.Т. Шрейнера. - Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. - 361 с.
7. Шрейнер Р.Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. - Екатеринбург УРО РАН, 2000. - 654 с.