В данной работе представлен способ управления движением автономного мобильного робота в относительной системе координат гравитационного и магнитного поля Земли. В процессе разработки были получены: общая структурная и функциональная схема мобильного робота, математические модели для определения координат и управления движением мобильного робота, и алгоритм функционирования мобильного робота.
Ключевые слова: навигация, автономный мобильный робот, относительная система координат, гравитационное поле Земли и магнитное поле Земли.
Одним из перспективных направлений проектирования мобильных роботов является обеспечение автономности перемещения в течение длительного интервала времени по неизвестной (недетерминированной) открытой или закрытой местности, без использования дополнительных технических средств навигации. Данный класс мобильных роботов позволит сравнительно недорого и без опасности для здоровья людей решать комплекс задач. Такие задачи встречаются во многих областях науки, техники и промышленности, в первую очередь там, где жизнедеятельность человека либо затруднена, либо вообще невозможна, например, в зонах радиоактивного или химического загрязнения, при проведении подводных или космических исследований, а также при решении задач, связанных с контролем, защитой и охраной окружающей среды, разведкой и картографией местности. Основной проблемой мобильных роботов является решение задачи навигации, что подразумевает локализацию и картографию рабочего пространства. Информация о локализации необходима для решения большинства задач управления: прохождение заданной траектории, поиск траектории к заданной точке, возвращение в исходное положение. Картография необходима для запоминания пройденного маршрута, планирования траектории в обход статических препятствий, слежения за динамическими объектами и т. д. Задача локализации является наиболее сложной, хотя она может быть решена при помощи датчиков, спутниковых навигационных систем GPS и ГЛОНАСС. Недостатком данных систем является низкая точность и ограничения доступности сигналов спутников, что делает невозможным определение положения робота внутри зданий, а также вблизи высоких сооружений или деревьев [1–3].
Однако, внутреннее строение Земли предоставляет идеальную систему координат, которая может быть использована для управления движением автономного мобильного робота. Данная система координат может быть сформирована за счет магнитного [4] и гравитационного поля Земли [5], которые присутствуют практически везде, а точность определения координат будет зависеть только от сложности программного и аппаратного обеспечения мобильного робота.
Формулирование задачи проектирования. В ситуациях отсутствия глобальных систем навигации (GPS и ГЛОНАСС) управление автономным мобильным роботом в неопределенном трехмерном пространстве становится проблематичным. Наличие подъемов и спусков на поверхности добавляют значительные ошибки в процессе навигации, что может привести к потере мобильного робота. С целью исключения данных недостатков предлагается способ управления движением автономного мобильного робота в относительной системе координат гравитационного и магнитного поля Земли.
Решение задачи проектирования. С целью достижения поставленной задачи в работе были реализованы следующие шаги: синтез общей структурной схемы, синтез функциональной схемы мобильного робота, синтез математической модели для определения координат и управления движением мобильного робота, и синтез алгоритма функционирования мобильного робота.
Общая структурная схема управления. На Рисунке 1 представлена общая структурная схема управления автономным мобильным роботом в относительной системе координат магнитного и гравитационного поля Земли. Схема содержит: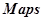 
— плоскость 
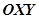которая представляет собой отображение трехмерного пространства 
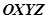, в котором перемещяется мобильный робот; 
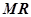— мобильный робот; 
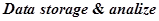— компьютер для определения заданий, сбора и анализа данных; 
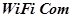— обмен данными между мобильным роботом и компьютером; 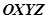— относительная система координат, центр которой является исходным положением мобильного робота 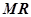перед началом движения; 
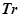— условная траектория движения мобильного робота для достижения точки 
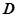с координатами 
.
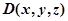Перед началом движения, мобильный робот 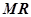получает от компьютера исходные координаты 
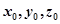, которые соответствуют центру относительной системы координат 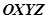и координаты точки назначения 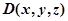, заданные на плоскости 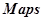. Так как, плоскость 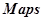это отображение трехмерного пространства 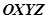, для инициализации процесса управления необходимо определить только 
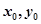и 
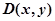. В процессе перемещения мобильного робота 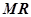происходит определение вектора направления движения 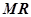по отношению к магнитному полю Земли и определение наклонности плоскости 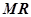по отношению к гравитационному полю Земли. Полученные данные используются для коррекции координат 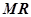на плоскости 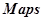и для вычисления следующего шага необходимого для перемещения 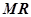с целью достижения точки .
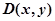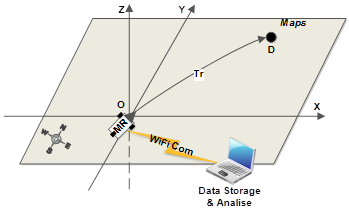
Рис. 1. Общая структурная схема управления автономным мобильным роботом в относительной системе координат магнитного и гравитационного поля Земли
Функциональная схема мобильного робота. В данной работе был рассмотрен мобильный робот 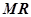, который представляет собой трехколесную структуру (Рисунок 2), где: 
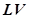и 
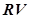— соответственно левое и правое ведущие колеса, соединенные с двигателями постоянного тока; 
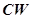— поворотное колесо для направления движения 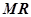налево или направо в зависимости от скорости вращения 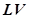и ;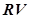 
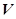— вектор направления движения мобильного робота .
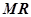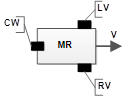
Рис. 2. Структура мобильного робота
Функциональная схема блока управления мобильным роботом представлена на Рисунке 3. Схема состоит из следующих компонентов:
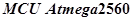— микроконтроллер фирмы Atmel [6];
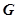— трехосевой гироскоп, модель L3G4200D [7];
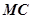— магнитный компас, модель MAG3110 [8];
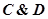— клавиатура для установки режимов функционирования и дисплей для отображения состояния блока управления;
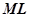и 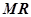— левый и правый двигатели постоянного тока, соответственно;
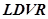и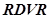 
— драйвер модели L298N [9] для управления двигателям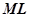и и 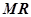при помощи широтно-импульсной модуляции (ШИМ);
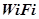— модуль для беспроводной коммуникации в сети, модель ESP8266 [10];
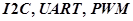и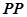 
— стандартные порты ввода/вывода микроконтроллера 
.
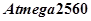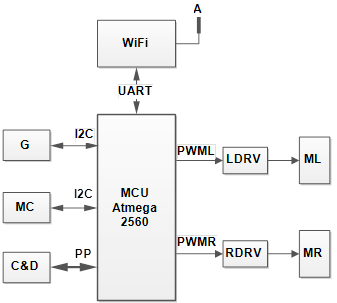
Рис. 3. Функциональная схема блока управления мобильным роботом
Математическая модель для определения координат и управления движением мобильного робота. Управление движением мобильного робота 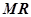осуществляется на основе текущих координат и конечных координат точки 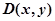. На Рисунке 4 представлена схема для вычисления координат мобильного робота на плоскости 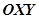в зависимости от координат в трехмерном пространстве 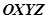, где: ось координат 
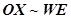(долгота, направление запад — восток) и 
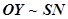(широта, направление юг — север), 
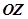— высота по отношению к точке 
;
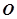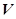— вектор направления движения мобильного робота в пространстве ;
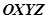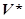— проекция вектора 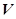на плоскости 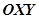, где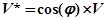 
;
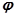— угол между вектором 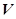и плоскостью 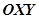, где 
, 
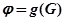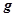— это функция преобразования данных от гироскопа 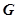в угол ;
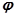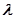— угол между вектором 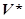и ось координат 
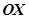, где 
, 
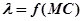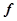— это функция преобразования данных от магнитного компаса 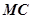в угол ;
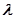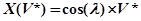— координата вектора 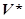по оси ;
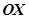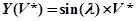— координата вектора 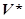по оси 
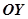[11].
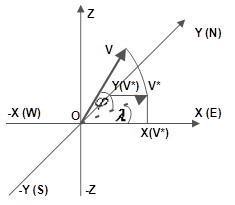
Рис. 4. Схема вычисления координат мобильного робота на плоскости
Из Рисунка 4 видно, что на каждом шаге управления происходит изменение координат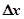 
и 
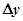, соответственно: 
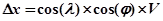и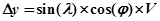 
.
Динамику перемещения мобильного робота можно представить следующей системой уравнений:
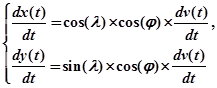(1)
В результате преобразования (1) получаем:
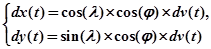. (2)
Интегрируя систему уравнений (2) получаем текущие координаты мобильного робота на плоскости :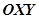
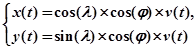(3)
где: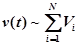
, 
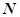— число шагов перемещения мобильного робота.
Имея текущие координаты мобильного робота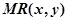 
и координаты цели 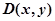можно составить уравнения для ШИМ управления двигателями 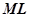и :
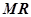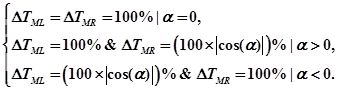(4)
В уравнениях (4) обозначено: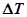 
— длительность импульса для ШИМ управления двигателям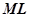и и ;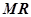 
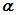— угол между вектором 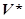и траектория .
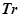Алгоритм функционирования мобильного робота. Алгоритм функционирования мобильного робота представлен на Рисунке 5, где: 1 — начало алгоритма; 2 — прием данных из сети 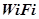для инициализации процесса перемещения; 3 — инициализация начальной точки 
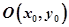и конечной точки 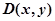; 4 — ввод данных с гироскопа 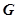; 5 — ввод данных с магнитного компаса 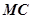; 6 — вычисление углов 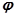и 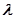; 7 — вычисление текущих координат мобильного робота; 8 — вычисление длительности ШИМ сигналов управления; 9 — вывод сигналов управления двигателями; 10 — передача текущих координат через сеть ; 11 — проверка условия конца алгоритма; 12 — конец алгоритма.
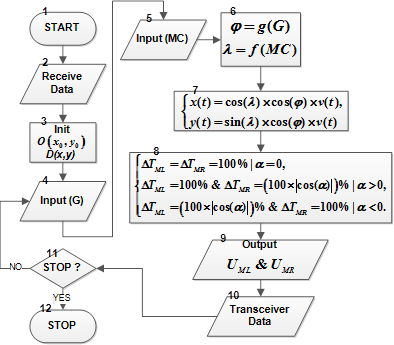
Рис. 5. Блок-схема алгоритма функционирования мобильного робота
Выводы. Основной целью данной работы является разработка способа управления автономным мобильным роботом используя магнитное и гравитационное поля Земли. Разработаный метод позволяет управлять движением робота в условиях ограниченого действия или полного отсутствия спутниковых навигационных систем GPS и ГЛОНАСС. Полученные результаты могут быть использованы для проектирования систем навигации мобильных роботов предназначеных для работы в местах недоступных для спутниковых сигналов или на других планетах при условии наличия магнитного и гравитационного поля.
Литература:
1. Герасимов, В.Н.; Михайлов, Б. Б. Решение задачи управления движением мобильного робота при наличии динамических препятствий. Вестник МГТУ им. Н. Э. Баумана. Сер. “Приборостроение”. 2012. стр. 83–92, ISSN 0236–3933.
2. Мартыненко, Ю. Г. Управление движением мобильных колёсных роботов // Фундаментальная и прикладная математика. 2005. Т. 11, Вып. 8. С. 29–80.
3. Ababii, V.; Sudacevschi, V.; Podubnii, M.; Cojuhari, I. Sensors network based on mobile robots. International Conference on DEVELOPMENT AND APPLICATION SYSTEMS 12th Edition, May 15–17, 2014, Suceava, ROMANIA, pp. 70–72, ISSN 1844–5039. DOI: 10.1109/DAAS.2014.6842430. In SCOPUS: (http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=6842430&sortType %3Dasc_p_Sequence %26filter %3DAND %28p_IS_Number %3A6842413 %29).
4. Дьяченко, А. И. Магнитные полюса Земли. Серия Математическое просвещение. М.: МЦНМО, 2003. — 48с., ISBN 5–94057–080–1.
5. Иваненко, Д. Д. Гравитация. Отв. ред. П. И. Фомин. — 5-е изд. — М.: Изд-во ЛКИ, 2012. — 200с., ISBN 978–5-382–01360–2.
6. http://www.atmel.com/devices/atmega2560.aspx, (Дата доступа 10.08.2015).
7. http://www.st.com/web/en/resource/technical/document/datasheet/CD00265057. pdf, (Дата доступа 14.08.2015).
8. http://www.chipdip.ru/product/mag3110-board/, (Дата доступа 17.08.2015).
9. http://tronixlabs.com/news/tutorial-l298n-dual-motor-controller-module-2a-and-arduino/, (Дата доступа 13.08.2015).
10. https://www.sparkfun.com/products/13678, (Дата доступа 01.08.2015).
11. Тимченко, Д. Н. Синтез логико-динамической системы оптимального управления нелинейным неголономным объектом типа «мобильный робот». // Технические науки в России и за рубежом: материалы междунар. науч. конф. (г. Москва, май 2011 г.). — М.: Ваш полиграфический партнер, 2011. — С. 43–48.
