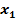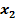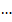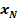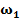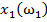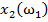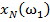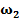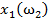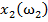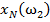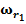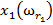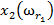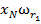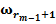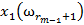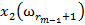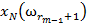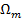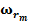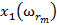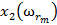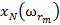В данной статье приводится математическая модель системы распознавания изображений, содержащих текстовую информацию или использующих такую информацию при своей генерации. Предполагается, что рассматриваемые системы будет основаны на возможностях нейронных сетей.
Ключевые слова:компоненты связности, нейронные сети, обучение с учителем, распознавание, сегментация.
В общем случае распознавание текста состоит из следующих процедур и методов:
1. Предварительная обработка.
2. Сегментация.
3. Распознавание.
Предварительная обработка представляет собой процесс последовательного применения фильтров и операций для усреднения и выравнивания гистограмм текстового изображения, а также для исключения содержащихся в нем помех и подавления шумов.
Сегментация является процессом разбиения изображения, содержащего текстовую информацию, на отдельные символы.
Входные данные для осуществления распознавания — это изображения, которые были получены в результате процессов предварительной обработки и сегментации.
Предварительная обработка
Предварительная обработка текстового изображения заключается в его нормализации, то есть, мы пытаемся очистить такое изображение от зашумляющих элементов, которые могут в нем содержаться.
Пусть:
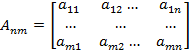 — текстовое изображение размера
— текстовое изображение размера 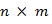 пикселей;
пикселей;
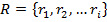 — множество грамматических правил, применяемых к
— множество грамматических правил, применяемых к 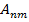 ;
;
Под методом предварительной обработки будем понимать отображение:
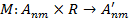
Функция 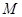 на основе требования
на основе требования 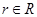 и информации о генерации
и информации о генерации 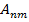 , подлежащей процедуре предварительной обработки, выполняет обработку исходного текстового изображения и формирование промежуточного изображения
, подлежащей процедуре предварительной обработки, выполняет обработку исходного текстового изображения и формирование промежуточного изображения 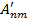 .
.
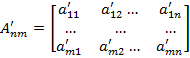 — промежуточное изображение размера
— промежуточное изображение размера 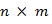 пикселей, полученное в ходе предварительной обработки.
пикселей, полученное в ходе предварительной обработки.
Сегментация
Сегментация представляет собой разделение изображения на однородные области. Существует множество методов сегментации. Метод на основе поиска компонент связности является одним из самых действенных в отношении изображений, содержащих текстовую информацию.
Сегментированное изображение задается парой — изображение и разметка на классы. 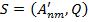 . Разметкой является матрица Q размерами
. Разметкой является матрица Q размерами 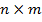 . Ее элементы — числа (1,..., 8).
. Ее элементы — числа (1,..., 8).
Введем понятие компоненты связности. Зададим граф смежности между пикселями с 8-связной системой соседства. Назовем окрестностью пикселя множество его соседей. Если один пиксель лежит в окрестности другого, то эти пиксели смежны. Пусть имеется множество пикселей V. V называется связным множеством, если любой пары пикселей 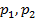 найдется последовательность пикселей
найдется последовательность пикселей 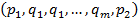 , в которой пиксели
, в которой пиксели 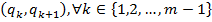 и
и 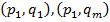 смежны [3].
смежны [3].
Таким образом, множество Q распадается однозначным образом на множество непересекающихся связных множеств 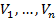 , которые называются компонентами связности множества Q.
, которые называются компонентами связности множества Q.
Каждая компонента связности представляет из себя пару (B, M): бинарную маску 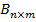 и метку класса M. Получаем, что:
и метку класса M. Получаем, что:
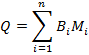
В итоге сегментированное изображение — это:
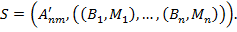
Предположим, что существует некоторая истинная сегментация для данного изображения 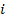 :
:
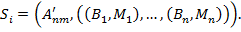
Сегментация, полученная неким алгоритмом на изображении 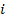 :
:
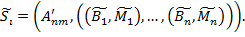
Распознавание
Распознавание (обучение с учителем) — отнесение предъявляемых объектов к определённым классам с помощью применения известных правил классификации [2]. Это наиболее типичная задача систем распознавания. Для того чтобы система могла выполнять данный функционал, необходимо провести ее обучение, используя большую выборку примеров, представляющую обучающую выборку объектов распознавания.
Формулировка задачи распознавания символов текстовых изображений представлена в таблице 1. Исходя из нее, для нашей работы была выбрана многослойная нейронная сеть с обратным распространением ошибки с обучением с учителем.
Таблица 1
Формулировка задачи распознавания символов
|
|
Задача распознавания букв |
Формулировка для нейронной сети |
|
Дано |
Черно-белое изображение единицы алфавита размером |
Входной вектор из |
|
Надо |
Определить, к какому символу алфавита относится входящий символ. Всего в алфавите |
Построить нейронную сеть с |
Дано множество M объектов ω. Объекты задаются значениями некоторых признаков 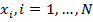 , наборы которых одинаковы для всех объектов. Совокупность признаков объекта ω определяет некоторым образом его описание
, наборы которых одинаковы для всех объектов. Совокупность признаков объекта ω определяет некоторым образом его описание 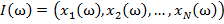 [1]. Признаки могут выражаться значениями из набора возможных вариантов языка
[1]. Признаки могут выражаться значениями из набора возможных вариантов языка 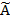 .
.
На всём множестве M существует разбиение на подмножества (классы объектов):
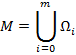
Разбиение на классы может быть задано полностью или определяться некоторой априорной информацией 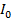 о классах
о классах 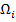 — например, характеристическим описанием входящих в них объектов.
— например, характеристическим описанием входящих в них объектов.
Задача распознавания состоит в том, чтобы для каждого данного объекта ω по его описанию 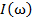 и априорной (обучающей) информации
и априорной (обучающей) информации 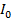 вычислить значения предикатов
вычислить значения предикатов
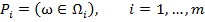
Для описания невозможности распознавания объектов предикаты 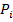 заменяются величинами
заменяются величинами 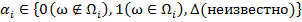 [1]. Таким образом, для рассматриваемого объекта ω необходимо вычислить его информационный вектор
[1]. Таким образом, для рассматриваемого объекта ω необходимо вычислить его информационный вектор 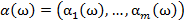 .
.
Процедура, строящая информационный вектор 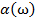 в данном случае выражает алгоритм принятия решения об отнесении объекта
в данном случае выражает алгоритм принятия решения об отнесении объекта 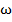 к тому или иному классу и называется «решающей функцией» [4].
к тому или иному классу и называется «решающей функцией» [4].
Альтернативой ручному вводу в систему описаний классов объектов и параметров решающей функции является обучение системы. Оно представляет собой процедуру самонастройки системы распознавания на основе воспринимаемой информации и может происходить как при подготовке системы, так и в процессе её работы по мере «накопления опыта».
Вид обучения, в котором системе представляется набор образцов распознаваемых объектов с указанием их принадлежности классам, называется обучением с учителем. Набор образцовых объектов называется обучающей выборкой. Необученная система производит распознавание предлагаемых объектов и сравнивает свои результаты с правильными ответами, поступающими от учителя. По результатам сравнения система корректирует параметры решающей функции.
Итак, обучающая выборка в задаче распознавания является априорной информацией о множестве распознаваемых объектов и представляет описание всех классов объектов [6]:
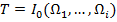
Её составляют описания предложенных учителем объектов с указанием их принадлежности классам, т. е. можно определить её как совокупность описаний объектов [1]:
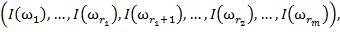
где объекты 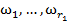 принадлежат классу
принадлежат классу 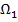 , объекты
, объекты 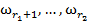 — классу
— классу 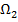 и т. д.
и т. д.
Таким образом, обучающая выборка представляет собой таблицу, строки которой помечены названиями объектов 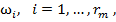 а столбцы — названиями признаков
а столбцы — названиями признаков 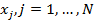 (см. таблицу 2). Элементами таблицы являются значения признаков объектов
(см. таблицу 2). Элементами таблицы являются значения признаков объектов 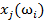 . Строки таблицы сгруппированы по классам
. Строки таблицы сгруппированы по классам 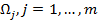 .
.
Таблица 2
Обучающая выборка
|
|
|
|
|
|
Классы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для обучения сети необходимо иметь множество пар векторов {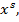
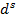 },
}, 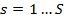 , где {
, где {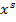 } = {
} = {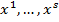 } — множество входных векторов
} — множество входных векторов 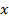 , {
, {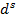 } = {
} = {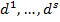 } — множество эталонов выходных векторов [5]. Совокупность пар {
} — множество эталонов выходных векторов [5]. Совокупность пар {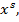
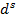 } образует обучающее множество.
} образует обучающее множество.
Количество элементов S в обучающем множестве должно быть достаточным для обучения сети, чтобы алгоритм смог сформировать набор параметров сети, выдающий в результате нужное отображение x → y. Количество пар в обучающем множестве не имеет четких значений. Однако если элементов слишком много или мало, сеть не обучится и не решит поставленную задачу. Выберем один из векторов 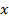 и подадим его на вход сети. На выходе получится некоторый вектор
и подадим его на вход сети. На выходе получится некоторый вектор 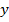 .
.
Для оценки качества обучения чаще всего выбирают суммарную квадратичную ошибку [2,5]:
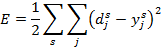
где 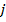 — число нейронов в выходном слое,
— число нейронов в выходном слое,
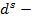 известное решение задачи
известное решение задачи 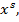
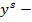 решение, полученное на выходе обученной нейронной сети.
решение, полученное на выходе обученной нейронной сети.
Данная оценка помогает подогнать входные данные алгоритма до оптимальных для повышения его качества.
Литература:
1. Журавлёв Ю. И. Распознавание. Классификация. Прогноз. Математические методы и их применение. Вып.2. М.: Наука, 1989. С.208–327.
2. Заенцев И. В. Нейронные сети: Основные модели. Воронеж, 1999, С.76.
3. Малышева Е. К. Автоматическая сегментация изображений рукописных документов. М., 2014.
4. Ту Дж., Гонсалес Р. Принципы распознавания образов. М.: Мир, 1978.
5. Сотник С. Л. Конспект лекций по курсу «основы проектирования систем искусственного интеллекта», Москва, 1998.
6. Riedmiller Martin, Braun Heinrich. A direct adaptive method for faster backpropagation learning: The RPROP algorithm // In Proceedings of the IEEE International Conference on Neural Networks, 1993.







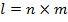 двоичных символов.
двоичных символов.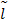 символов.
символов.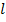 входами и
входами и 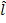 выходами, которые помечены как символы алфавита. Таким образом, если на входе изображение символа «А», то максимальное значение выходного сигнала достигается на выходе «А». Аналогично сеть работает для всех
выходами, которые помечены как символы алфавита. Таким образом, если на входе изображение символа «А», то максимальное значение выходного сигнала достигается на выходе «А». Аналогично сеть работает для всех