Введение.Во многих прикладных задачах биологии и медицины приходится рассматривать большое число факторов, оказывающих сложное, разнонаправленное влияние, как на результирующий показатель, так и друг на друга. ИНС как метод мягких вычислений позволяет, не выполняя детального исследования всех величин, влияющих на результат, всё же получить прогноз. Целью работы является предложение ИНС – модели и применение её на практике.
Модель. В предлагаемой ИНС - модели функциональных взаимосвязей нейрон NpTij – это двоичный элемент, NpTij =1, если актуализируется j-я функциональная модель влияния на показатель p на временном отрезке в окрестности Ti. Функциональную модель влияния будем называть уравнением влияния. В противном случае, те, если уравнение влияния не актуально, нейрон равен нулю. Вес, который имеет связь нейронов, будет ненулевым, если два уравнения влияния связывает факт выполнения в последовательные моменты времени. Чем чаще этот переход происходит на практике, тем больше вес связи. Калибровка весов производится по формуле:
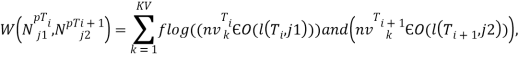 ( 1)
( 1)
Здесь k-е наблюдение является временным рядом; flog(true)=1,flog(false)=0; O(x)- окрестность x; nvTik- значение i-го элемента k-го временного ряда; l(T,j)- ограничение на значение p- го показателя в j-м уравнении влияния для момента T. По сути, предлагается другое использование уравнений влияния, которые не редко являются самым перспективным результатом исследования биологического процесса, но их практическое применение ограничено наличием большого числа не до конца известных ограничений на значения параметров. Этот недостаток преодолевался либо посредством построения более общей модели , либо уточнением трактовки результатов с помощью аппарата математической статистики.
Примеры применения ИНС-модели. Пример 1. Прогноз роста малоинвазивной опухоли с учетом фактора эндотелия сосудов. ИНС- модель строится на основе данных и выводов, полученных при построении общей модели, в идеале охватывающей все факторы[1]. В [1] опухоль рассматривается как колония клеток, окруженная нормальной тканью. Живые клетки опухоли могут находиться в двух состояниях: пролиферирующие клетки с плотностью n1(t) (t - время) делятся с постоянной скоростью и не диффундируют, мигрирующие клетки с плотностью n2(t) диффундируют и не делятся. Интенсивности переходов из одного состояния в другое ( P1(S) и P2(S)) зависят от концентрации глюкозы S (t), когда ее много, мигрирующие клетки активно переходят в пролиферирующее состояние, а при значительном снижении ее концентрации клетки перестают пролиферировать и мигрируют случайным образом, при дальнейшем снижении - гибнут. Глюкоза диффундирует в ткани с постоянным коэффициентом и потребляется как злокачественными, так и нормальными клетками организма. Мигрирующие клетки влияют на фактор роста эндотелия сосудов, который усиливает плотность сосудистой сети, и, как следствие, увеличению концентрации глюкозы. Повышение плотности пролиферирующих клеток снижает концентрацию глюкозы. С учетом этих и других факторов уравнения для клеток опухоли описывается системами дифференциальных уравнений. Два уравнения первой системы модели [1, с.366] :
![]() , (2)
, (2)
Используем следующую аппроксимацию S(t) и n1(t) (ниже KCindex – параметры):
n1(t)=KC3(t-KC1)( t-KC2)2, S(t) =KC4ln(t). (3)
Нетрудно убедиться, что модель (3), дополненная необходимыми ограничениями, не противоречит модели [1], и при этом отражает биологические данные о том, что повышение концентрации глюкозы вызывает рост плотности пролиферирующих клеток, особенно резкий после прохождения некоторого предела (см. рис. 1.A.)
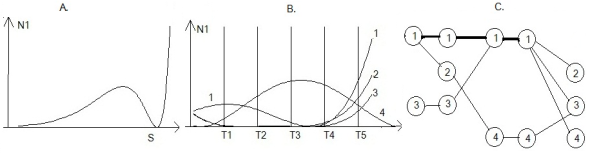
Рис.1. Этапы разработки ИНС-модели роста малоинвазивной опухоли
При переходе к вычислительной процедуре используем гипотетические значения KCi (табл.1, рис.1.B.).В ИНС-модели p=1, показатель - n1 ,уравнения влияния: l(T,1)=1; l(T,2)=13, l(T,3)=8; l(T,4)=20.
Таблица 1
Расчёт параметров ИНС-модели
|
Ti |
Nv |
l |
j |
nv |
l |
j |
nv |
l |
j |
nv |
l |
j |
|
KC1=120, KC2=-28 |
KC1=36, KC2=56 |
KC1=30, KC2=70 |
KC1=6, KC2=126 |
|||||||||
|
1 |
10 |
8 |
3 |
0 |
1 |
1 |
0 |
1 |
1 |
3 |
1 |
1 |
|
2 |
7 |
8 |
3 |
0 |
1 |
1 |
0 |
1 |
1 |
14 |
13 |
2 |
|
3 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
21 |
20 |
4 |
|
4 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
19 |
20 |
4 |
|
5 |
21 |
20 |
4 |
13 |
13 |
2 |
7 |
8 |
3 |
9 |
8 |
3 |
Используя (1) , получаем: W(N11,N21)=2; W(N21,N31)=2; W(N31,N41)=3. Прочие веса между связанными нейронами (см. рис.1.С.) равны единице. Прогноз основывается на том, что текущее состояние больного, описанное в форме актуальных уравнений влияния, определяет дальнейшее возбуждение сети, а значит и, последовательность возможных состояний. Пример 2. Пусть по результатам исследования известна форма зависимости показателя, разная для разных значений параметров. Построим ИНС, называемую персептрон. Сенсорный слой – входные значения параметров, ассоциативный слой – нейроны A, отражающие актуальность уравнений влияния. На внешнем слое – решающие элементы R, веса связей A и R элементов подобраны так, чтобы получить ответ на вопрос в форме определения класса входных данных, этот результат даёт стандартная процедура обучения. Чтобы использовать модель для работы с реальными данными, предлагаем использовать нечёткий вывод и с его помощью отобразить вектор параметров одного больного в подмножество обучающего множества векторов сенсорного слоя, которое может рассматриваться как неполное изображение, подлежащее распознаванию.
Обозначим через X вектор параметров. Нечёткое отношение N осуществляет отображение переменной Xt больного t универсума X0 в переменную Yt универсума Y0 ,Xt формируется стандартной процедурой фазификации на X0, {x0i – выбранное значение i-го параметра}. Y0={y0j}, y0j-j-е уравнение влияние. Nij- частота, с которой x0iнаходится достаточно близко от значения i-й пары параметр-значение при выполнении j-го уравнения влияния. Переменная Yt дефазифицируется сопоставлением µj с порогом Θ. Ненулевые значения вектора определяют подмножество уравнений влияний, которые объединяет актуальность, так определяются значения А-элементов. Обратимся к реальным данным. Исследуются различные особенности гемопоэтических нарушений у больных вторичным миелодиспластическим синдромом[2]. Требуется определить риск МДС IPPSS, если у больного бластных клеток -12 % и кариотип – аномалии 5-й хромосомы. Пусть уравнение влияния – диагноз, Θ=0.5. Данные взяты из [2, с.140].
Таблица 2
Матрица элементов нечёткого отношения Nij и параметров персептрона
|
Характеристики: 1.Кариотип 2.Кол-во бласт-х клеток в костном мозге(%) |
µ(Yt) |
0.48(0) |
0.58(1) |
0.46(0) |
0.62(1) |
|
µ(Xt) |
Множеств. миелома |
Лимфома Ходжкина |
Неходж-е лимфомы |
Комбиниров-я терапиия |
|
|
i\j |
j=1, A1 |
j=2, A2 |
j=3, A3 |
j=4, A4 |
|
|
1.1-аномалии 5 хромосомы 1.2- прочее |
1 0 |
0/3=0 3/3=1 |
1/12=0.08 11/12=0.92 |
0/13=0 13/13=1 |
0/13=1 13/13=1 |
|
2.3 5-10 2.4 11-19 2.5 20-29 |
0.81 0.87 0.48 |
0 1/3=0.33 2/3=0.66 |
7/12=0.58 4/12=0.33 1/12=0.08 |
4/13=0.31 6/13=0.46 3/13=0.23 |
8/13=0.62 2/13=0.15 1/13=0.08 |
|
Риски МДС IPPSS |
Веса связи A-элементов с R- элементами персептрона |
||||
|
Низкий Высокий |
W1j W2j |
0 3*24/18=4 |
7 6*24/18=8 |
8 5*24/18=6.67 |
9 4*24/18=5.33 |
По результатам (табл.2) имеем A=(0,1,0,1), R1 =16 и R2=13.33. Отсюда следует , что для больного риск МДС IPPSS низкий, тк R1>R2.
Заключение. С нашей точки зрения в моделировании биологических процессов представляет интерес применение ИНС-моделирования и других методов мягких вычислений. Это объективно обусловлено тем, что специфика объекта моделирования приводит к появлению NP-сложности, те ситуации, когда алгоритмический класс необходимо учитывать для корректной постановки и корректного решения задачи.
Литература:
- Колобов А.В., Кузнецов М.Б. Математическое моделирование роста малоинвазивной опухоли с учётом инактивации антиангиогенным препаратом фактора роста эндотелия сосудов //Компьютерные исследования и моделирование. 2015 г. Т. 7. № 2. С. 374–381.
- Шатохин Ю.В., Снежко И.В., Куцев С.И., Сизякина Л.П., Кузуб Е.И., Шатохина О.Н.,Гранкина Е.А. Клинико-морфологические, иммунологические особенности гемопоэтическим нарушений у больных вторичным миелодиспластическим синдромом//Цитокины и воспаление. 2010. Т. 9. № 4. С. 139-142.







