Одной из дисциплин, изучаемых студентами бакалавриата, обучающимися по направлению «Программная инженерия», является «Тестирование программного обеспечения». Известно, что тестирование представляет собой один из этапов жизненного цикла разработки программного обеспечения и важнейшую составляющую обеспечения качества программного обеспечения [1, 2].
В ходе одной из лабораторных работ студент должен научиться производить тестирование программного обеспечения способом тестирования базового пути [1, 3].
Рассмотрим некоторые особенности разработанного методического пособия по данной теме. В разделе «Краткие теоретические сведения» методического пособия представлена необходимая теория, посвященная данному способу тестирования, сопровождаемая примерами. Далее рассмотрим содержание этого раздела, основанное на работе [1].
Тестирование базового пути — это способ тестирования, который основан на принципе «белого ящика». Автор этого способа — Том МакКейб (1976 г.).
Следует отметить, что при использовании тестирования «белого ящика» как одного из принципов тестирования, известна внутренняя структура программы, а исследуются внутренние элементы программы и связи между ними.
Способ тестирования базового пути дает возможность получить оценку комплексной сложности программы, а затем использовать эту оценку для определения необходимого количества тестовых вариантов.
Тестовые варианты разрабатываются для проверки базового множества путей (маршрутов) в программе. Они гарантируют однократное выполнение каждого оператора программы при тестировании.
Для представления программы при использовании данного способа тестирования используется потоковый граф.
Потоковый граф строится отображением управляющей структуры программы. В ходе отображения закрывающие скобки условных операторов и операторов циклов рассматриваются как отдельные (фиктивные) операторы.
Узлы (вершины) потокового графа соответствуют линейным участкам программы, включают один или несколько операторов программы.
Дуги потокового графа отображают поток управления в программе (передача управления между операторами).
Различают операторные и предикатные узлы. Из операторного узла выходит одна дуга, а из предикатного — две дуги.
Предикатные узлы соответствуют простым условиям в программе. Составное условие программы отображается в несколько предикатных узлов. Составным называют условие, в котором используется одна или несколько булевых операций (конъюнкция, дизъюнкция).
Замкнутые области, образованные дугами и узлами, называют регионами. Окружающая граф среда рассматривается как дополнительный регион.
Рассмотрим пример построения потокового графа. Дана программа, написанная на языке Pascal [4] в системе «Pascal ABC» [5] (рис. 1).

Рис. 1. Пример программы на языке Pascal
С целью построения потокового графа (рис. 2) операторы программы на рис. 1 пронумерованы с использованием комментариев. Следует отметить, что некоторые операторы, составляющие единый линейный участок программы, объединены в один узел (например, три идущих подряд оператора присваивания обозначены цифрой 1, а три идущих подряд оператора вывода — цифрой 9).
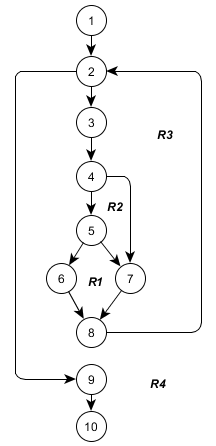
Рис. 2. Потоковый граф
Следует обратить внимание, что составное условие (a>0) and (a<7), согласно правилам построения потокового графа, отображается в два предикатных узла, а именно в узел 4, соответствующий простому условию a>0, и узел 5, соответствующий простому условию a<7.
В приведенном на рис. 2 потоковом графе:
1) 10 вершин (узлов), обозначенных кружками (все они пронумерованы в соответствии с нумерацией операторов в программе), каждая из которых соответствует линейному участку программы, включает один или несколько операторов;
2) 12 дуг (обозначенных стрелками), отображающих поток управления в программе;
3) 3 предикатных узла, соответствующих простым условиям в программе: a>b, a>0 и a<7.
4) четыре региона: замкнутые области, образованные дугами и узлами (обозначены как 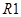 ,
, 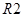 ,
, 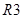 ) и окружающая граф среда (
) и окружающая граф среда (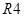 ).
).
Цикломатическая сложность — это метрика программного обеспечения, которая обеспечивает количественную оценку логической сложности программы. В способе тестирования базового пути цикломатическая сложность определяет:
1) количество независимых путей в базовом множестве программы;
2) верхнюю оценку количества тестов, которое гарантирует однократное выполнение всех операторов.
Независимым называется любой путь, который вводит новый оператор обработки или новое условие. В терминах потокового графа независимый путь должен содержать дугу, не входящую в ранее определенные пути.
Путь начинается в начальном узле, а заканчивается в конечном узле графа. Независимые пути формируются в порядке от самого короткого к самому длинному.
Перечислим независимые пути для потокового графа на рис. 2:
Путь 1: 1–2-9–10.
Путь 2: 1–2-3–4-7–8-2–9-10.
Путь 3: 1–2-3–4-5–7-8–2-9–10.
Путь 4: 1–2-3–4-5–6-8–2-9–10.
Заметим, что каждый новый путь включает новую дугу.
Все независимые пути графа образуют базовое множество.
Свойства базового множества:
1) тесты, обеспечивающие его проверку, гарантируют:
а) однократное выполнение каждого оператора;
б) выполнение каждого условия по true-ветви и по false-ветви;
2) мощность базового множества равна цикломатической сложности потокового графа.
Ценность 2-го свойства заключается в том, что оно дает оценку количества независимых путей, которое имеет смысл искать в графе.
Цикломатическая сложность вычисляется одним из трех способов:
1) Цикломатическая сложность равна количеству регионов потокового графа.
2) Цикломатическая сложность определяется по формуле:
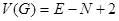 , (1)
, (1)
где 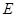 — количество дуг потокового графа
— количество дуг потокового графа 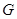 ;
;
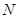 — количество узлов потокового графа
— количество узлов потокового графа 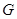 ;
;
3) Цикломатическая сложность формируется по формуле:
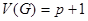 , (2)
, (2)
где 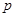 — количество предикатных узлов в потоковом графе
— количество предикатных узлов в потоковом графе 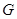 .
.
Вычислим цикломатическую сложность графа, изображенного на рис. 2, каждым из трех способов:
1) Потоковый граф имеет 4 региона (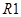 ,
, 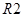 ,
, 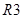 ,
, 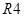 ), следовательно, цикломатическая сложность равна
), следовательно, цикломатическая сложность равна 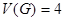 .
.
2) Количество дуг в потоковом графе равно 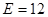 , а количество вершин -
, а количество вершин -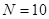 , следовательно, согласно формуле (1), цикломатическая сложность равна):
, следовательно, согласно формуле (1), цикломатическая сложность равна):
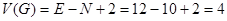 .
.
3) Количество предикатных узлов в потоковом графе равно 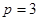 , следовательно, согласно формуле (2), цикломатическая сложность равна:
, следовательно, согласно формуле (2), цикломатическая сложность равна:
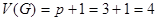 .
.
Таким образом, цикломатическая сложность потокового графа, изображенного на рис. 2, равна 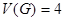 .
.
Как видно из выше изложенного, в разработанном методическом пособии в компактном виде изложена необходимая теория, посвященная основным понятиям и формулами, связанным со способом тестирования базового пути, снабженная достаточным количеством примеров. Продолжение данного исследования будет представлено в следующей статье.
Литература:
1. Орлов С. А., Цилькер Б. Я. Технологии разработки программного обеспечения: Учебник для вузов. 4-е изд. Стандарт третьего поколения. СПб.: Питер, 2012. 608 с.
2. Файзрахманов Р. А., Мурзакаев Р. Т., Брюханова А. А. Командная разработка и непрерывная интеграция в системах автоматизированного проектирования фигурного раскроя // Научное обозрение. 2015. № 1. С. 95–101.
3. Полевщиков И. С. Разработка методического пособия на тему «Тестирование базового пути» (для студентов бакалавриата направления «Программная инженерия») // Педагогика и современность. 2013. № 4. С. 83–85.
4. Полевщиков И. С. Особенности проведения лабораторной работы по дисциплине «Информатика» на тему «Структура программы на языке Паскаль. Процедуры ввода-вывода» для студентов бакалавриата // Молодой ученый. 2014. № 3. С. 69–72.
5. Система программирования Pascal ABC. URL: sunschool.mmcs.sfedu.ru/8-stranitsy-na-sajte/5-pabc. (Дата обращения: 30.08.2014).







