В статье рассматриваются явные формулы многомерной хаотической интерполяции функций многих переменных. Для нихпостроеныалгоритмыи программы.
Ключевые слова: многомерная интерполяция на хаотической сетке узлов.
In the article we consider the problem of interpolation function of many variables. For them are build the algorithms and programs.
1. Введение. Задача интерполяции является одной из основных задач численных методов. С её помощью решаются задачи приближённого аналитического представления, дифференцирования, интегрирования таблично заданных функций или функций со сложным аналитическим представлением. В настоящее время она применяется в проектировании самолётов, кораблей, деталей сложной формы, в компьютерной графике.
Задача интерполяции для функций многих переменных формулируется следующим образом. В области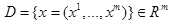 
, m-мерного евклидова пространства
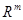c нормой 
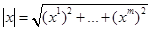, заданы точки (узлы) интерполяции, и значения 
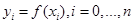,некоторой функции 
.
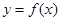Требуется найти интерполяционную функцию
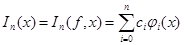, (1)
такую, что выполнялись условия интерполяции:
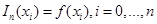. (2)
До 1960 годах в основном рассматривалась задача интерполяции функции от одной переменной. Интерполяционная формула строилась в виде линейной комбинации чебышевской системы функций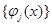 
, для которой
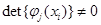,и задача (2) для любых множества точек интерполяции разрешима однозначно.Самыми ивестными являются формулы интерполяции Ньютона, Лагранжа, Гаусса,Эрмита, Стирлинга, Бесселя, Эверетта, Тиле. Приведем интерполяционные формулы Ньютона и Лагранжа:
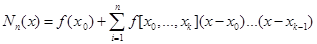, (3)
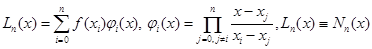, (4)
где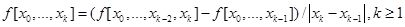
. Известная теорема Мейерхьюбера, о том, что если D замкнутое ограниченное множество, то в пространстве непрерывных функций С(D) нет чебышевской системы функций размерности больше единицы, в некоторое время задерживала поиск многомерных интерполяционных формул.
С 1960 года в задаче интерполяции появились сплайны, представляющие, в простейшем случае, кусочно-полиномиальные гладкие функции. Сплайны являются оптимальными в классе интерполяционных формул, например,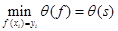 
, где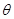 
-некоторый квадратичный функционал [5,6,7].
В связи с этим, сплайнами начали называть решения подобных вариационных задач. Такой подход оказался плодотворным, и позволил решить даже многомерную интерполяционную задачу, правда позволил найти неявную интерполяционную формулу. Явные интерполяционные формулы всё же создавались, но они едва были заметны в фоне модных сплайновых интерполяционных формул.
Известны следующие интерполяционные формулы и схемы:
1) интерполяционная формула Березина-Жидкова (1959):
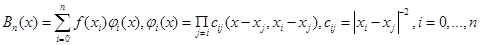. (5)
2) интерполяционная формула Шепарда (1965):
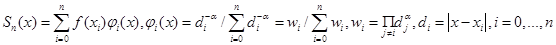(6)
3) интерполяционная схема Лебедева (1975)
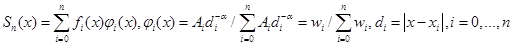(7)
где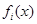 
-отрезок
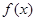по формуле Тейлора типа: 
.
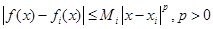4) весовая интерполяционная схема Франка:
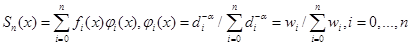, (8)
5) обобщённая интерполяционная формула типа Ньютона [3,4]:
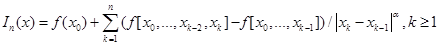, (9)
где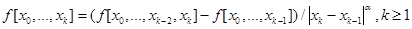 
- разделённые разности.
6) обобщённая интерполяционная формула типа Лагранжа [3,4]:
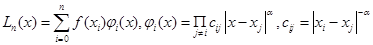. (10)
7) интерполяционная схема [3,4]:
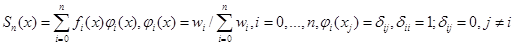. (11)
В частности,можно принять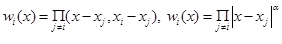 
.
8) обобщённая схема Эйткена [3,4] вычисления интерполяционной формулы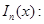 
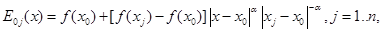
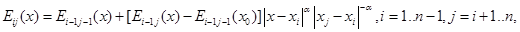(12)
В результате вычислений получаем: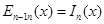 
.
2. Оценки остаточных членов. Для всех интерполяционных формул можно дать выражение для остаточного члена.
Лемма. Пусть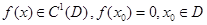 
. Тогда существует функция 
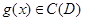такая, что 
.
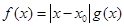Доказательство. По формуле конечных приращений Лагранжа и используя выражения для скалярного произведения в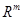 
имеем:
.
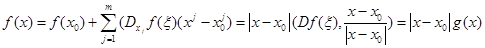Теорема 1. Пусть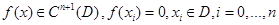 
. Тогда существует функция 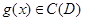такая, что 
.
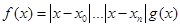Доказательство вытекает последовательным применением леммы. Из леммы вытекает что, для малости остаточного члена, необходимо хорошая гладкость, как самой интерполируемой функции, так и интерполяционной формулы.
Для интерполяционной формулы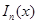
выражение остаточного члена находиться достаточно просто.
Теорема 2. Пусть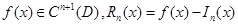 
. Тогда справедливо равенство
.
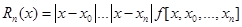Доказательство. Согласно определению разделённых разностей имеем,
.
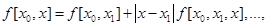
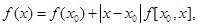
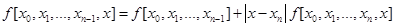Каждую следующую формулу подставляем в предыдущую и получаем:
.
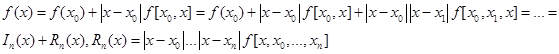3. Программы на языке Паскаль. Приведём программу построения .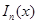
Newtoninterpolation;
type vec=array[0..100] of real; var i,j,n:integer;x1,x2,y,f:vec;p,c,In,t1,t2:real;
function d(u,v:real):real; begin d:=(u*u+v*v) end;
procedure tab(n:integer;var x1,x2,y:vec);
var i:integer;
begin for i:=0 to n do begin writeln('x1,x2,y[',i,']=');read(x1[i],x2[i],y[i]); end; end;
procedure Newton(n:integer;x1,x2,y:vec;u,v:real;var In:real);
var i,j:integer;
begin In:=f[0];p:=1;
for i:=0 to n-1 do for j:=i+1 to n do f[j]:=(f[j]-f[i])/d(x1[j]-x1[i],x2[j]-x2[i]);
for i:=1 to n do begin p:=p*d(t1-x1[i],t2-x2[i]);In:=In+f[i]*p end;
end;
begin
write('n=?');readln(n);tab(n,x1,x2,y);
repeat write('t1,t2=?');read(t1,t2); for i:=0 to n do f[i]:=y[i];
Newton(n,x1,x2,f,t1,t2,In); writeln('In(',t1,t2,')=',In);
until false; end.
Литература:
1. Имомов А. Формулы интерполирования функций многих переменных.Вычислительные системы, Новосибирск,1978, вып.75, с.50–55.
2. Имомов А. Явные формулы интерполирования функций многих переменных.Вычислительные системы, Новосибирск,1986, вып.115, с.93–97.
3. Имомов А. Интерполяция операторов. Научный вестник ФерГУ, Фергана, 1997, вып.1–2, с.57–62.
4. Имомов А. Явные интерполяционные формулы для функций многих переменных. Методы сплайн функций. Тезисы докл. Новосибирск, Изд. ИМ, 2001, с.38–39.
5. Schumaker L. L. Fitting surfaces to scattered data. In Approximation theory II. Acad.Press, New York-London, 1976, p. 203–268.
6. Barnhill R. E. Representation and approximation of surfaces. In Mathematical software III. Acad.Press, New York-London, 1977, p. 69–120.
7. Duchon J. Interpolation des fonctions de deux variables suivant le principe de la flexion des plaques minces.R. A. I.R. O. Analyse numerique.vol.10.n0 12.decembre 1976,p.5 a 12.
