Обработка экспериментальных данных методом дисперсионного анализа с однолетними культурами



В своих работах мы с коллегами не раз обращались к тематике обработки экспериментальных данных различными методами дисперсионного анализа.

Дисперсионный анализ по неортогональным и ортогональным схемам однофакторного и двухфакторного опыта ранее мы проводили для экспериментальных данных учетов плодовых растений. Это были высоты штамбов саженцев яблонь, площадь их листовой поверхности, количественное содержание антоцианов в плодах и др.

В этой работе интересным на мой взгляд показалось проведение дисперсионного анализа для обработки экспериментальных данных однофакторного опыта, исследуя однолетние культуры.

Было изучено действие подкормок на урожай капусты.

1. Урожай стандартных кочанов капусты (ц с 1 га)

Варианты	Повторения					Число наблюдений
	I	II	III	IV	V
1	560	542	574	537	510	5
2	548	509	560	-	497	4
3(st)	595	569	631	515	501	5
4	607	594	612	586	574	5
5	629	601	-	-	597	3
6	518	502	549	518	499	5
Суммы по повторениям с полным набором вариантов (1+3+4+6)	2280	2207	2366	2156	2084	-
Средние по 4 вариантам	570	552	592	539	521	-

В варианте 2 выпала из учета делянка в IV, а в варианте 5-делянка в III и IV повторениях (табл. 1). Прежде чем проводить дисперсионный анализ данных, необходимо привести результаты опыта к сравнимому виду, т. е. «восстановить» выпавшие данные.

1) В таблицу 1 записывают суммы по повторениям, включая те варианты, которые имеют полный набор делянок (варианты I, 3, 4 и 6), рассчитывают средние по повторениям путем деления сумм на число вариантов, имеющих полный набор дат, т. е. на 4.

2) Для вычисления теоретически ожидаемых урожаев на выпавших из учета делянках составляют вспомогательную таблицу 2, куда вносят поделяночные урожаи вариантов, в которых имеются выпавшие делянки, и средние по повторениям, вычисленные для вариантов с полным набором дат (из табл. 1).

2. Вспомогательная таблица для восстановления выпавших данных

Варианты	Повторения, Х					Суммы
	I	II	III	IV	V
2	548	509	560	-	495	2112
5	629	601	-	-	597	1827
Средние по 4 вариантам	570	552	592	539	521	-
Эффекты вариантов	-	-	-	-	-	-
Восстановленный урожай
2	-	-	-	528	-	-
5	-	-	457	761	-	-

Восстанавливать утраченные даты я предлагаю по формуле

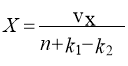
В рассматриваемом примере с использованием этой формулы получаем:

для второго повторения первого варианта:

;

для шестого повторения первого варианта:

;

для третьего повторения третьего варианта:

Таким образом, для восстановления выпавших данных предлагаемым способом необходимо по каждому варианту, где имеются утраченные величины, найти сумму элементов (), а затем вычислить необходимые величины, разделив значение полученной суммы на , где n-количество не выпавших в варианте величин, k_{1 —} количество величин которые ещё необходимо восстановить, k_{2 —} количество уже восстановленных значений. Причём при случае вычисления 2-й, 3-й и т. д. выпавших величин (кроме 1-й) в одном варианте, восстановленные до этого величины мы добавляем в сумму V_Х. Данный способ применим к величинам, имеющим нормальное распределение, к которым относятся фактически все основные показатели роста, развития и плодоношения сельскохозяйственных культур.

3) Составляют расчетную таблицу для дисперсионного анализа, в которой восстановленные урожаи заключают в скобки, подсчитывают суммы u средние по вариантам, суммы по повторениям, общую сумму и общий урожай по опыту (табл. 3). Правильность расчетов проверяют по соотношению ΣР=ΣV=16590

3. Урожай стандартных кочанов капусты (ц с 1 га)

Варианты	Повторения, Х					Суммы V	Средние
	I	II	III	IV	V
2	560	542	574	537	510	2723	544,6
1	548	509	560	(528)	497	2642	528,4
3(st)	595	569	631	515	501	2811	562,2
4	607	594	612	586	574	2973	594,6
5	629	601	(457)	(571)	597	2855	571,0
6	518	502	549	518	499	2586	517,2
Суммы Р	3457	3317	3383	3255	3178	ΣХ=16590	=553,3

4) Для вычисления сумм квадратов исходные даты целесообразно преобразовать по соотношению Х, = Х-А, приняв за условное среднее число 550,близкое к среднему урожаю по опыту. Преобразованные даты записывают в таблицу 4, суммируют даты по вариантам, повторениям и находят общую сумму ΣP=ΣV=ΣX₁=90

4. Таблица преобразованных дат

Варианты	Х1=Х-550					Суммы V
	I	II	III	IV	V
2	10	-8	24	-13	-40	-27
1	-2	-41	10	(-22)	-53	-108
3(st)	45	19	81	-35	-49	61
4	57	44	62	36	24	223
5	79	51	(-93)	(21)	47	105
6	-32	-48	-1	-32	-51	-164
Суммы Р	157	17	83	-45	-122	90= ΣХ1

Вычисляют суммы квадратов отклонений:

N=l*n=6*5=30

C=(ΣХ₁)²:N=(295)²:30=270

C_y= ΣХ₁²- C= (10²+8²+…+51²)-270 =58156–270=57886

C_p= ΣP²:Р-C=(157²+17²+…+122²):6–270=1353,8–270=1083,8

C_v= ΣV²:n-C=(27²+108²+…+164²):5–270=2702,9–270=2432,9

C_z=C_y-C_p-C_v= 57886–1083,8–2432,9=2369,3

Полученные данные заносят в таблицу дисперсионного анализа и вычисляют значение f-критерия. При вычислении числа степеней для остатка необходимо остаточное число степеней свободы, которое определяется обычным путем, уменьшить на число выпавших дат, в нашем примере на 3 даты (табл.5)

5 Результаты дисперсионного анализа

Дисперсия	Сумма квадратов	Степени свободы	Средний квадрат	Fф	F05
Общая	57886	29	-	-	-
Повторений	1083,8	4	-	-	-
Вариантов	2432,9	5	486,6	24,8	2,81
Остаток (ошибки)	2369,3	20–3=17	139,4	-	-

Значение F₀₅ будет из таблицы для 5 степеней свободы вариантов (числитель) и 17 степеней остатка (знаменатель).

Между вариантами имеются значимые на 5 % -ном уровне разности (F_ф> F₀₅), Н₀ отвергается.

5) Определение существенности частных различий в опыте с восстановленными урожаями имеет ту особенность, что необходимо учитывать число фактических дат, лежащих в основе вычисления статистических показателей. Вычисляют:

а) среднюю ошибку опыта

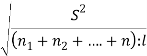= = =5,6ц

б) ошибки разности при сравнении вариантов 1,3,4 и 6 (n=5)

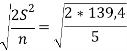= =7,4ц

варианта 2 (n=4) с вариантами 1,3,4 и 6 (n=5)

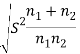== = 7,9 ц

варианта 5 (n=3) с вариантами 1,4 и 6 (n=5)

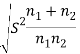== = 8,6 ц

в) наименьшие существенные разности для 5 %- ного (или 1- %- ного) уровня значимости:

НСР^/₀₅= t₀₅=2,11*7,4=15,6 ц

НСР^//₀₅ = t₀₅=2,11*7,9=16,7 ц

НСР^///₀₅ = t₀₅= 2,11*8,6=18,1 ц

Значение t₀₅ = 2,11 берут из таблицы 1 приложений для 17 степеней свободы остатка. Итоговая таблица результатов опыта и статистической обработки при сравнении опытных вариантов со стандартом имеет следующий вид:

6. Урожай стандартных кочанов капусты (ц с 1 га)

Варианты (сорта)	Урожай	Отклонение от стандартов	НСР0–5	Группа
3(st)	562,2	-	-	st
1	528,4	-33,8	15,6	III
2	544,6	-17,6	16,7	II
4	594,6	32,4	15,6	I
5	571,0	18,8	18,1	I
6	517,2	45,0	15,6	I

Можно сделать вывод. Существенную прибавку урожая обеспечит 4, 5,6-й варианты опыта (I группа), 2-й вариант по урожаю не отличается от стандарта (II группа), а 1-й вариант существенно уступает стандарту (III группа).

Литература:

1. Фролова, С. В. Статистические методы обработки экспериментальных данных в сельскохозяйственных исследованиях / С. В. Фролова, Л. И. Никонорова, Л. В. Бобрович и др. // Технические науки: теория и практика: Материалы Междунар. науч. конф. (г. Чита, апрель 2012 г.). — Чита, 2012. — С. 133–135.
2. Фролова, С. В. Вариационно-статистическая обработка экспериментальных данных при изучении качественных признаков сельскохозяйственных культур / С. В. Фролова, Л. И. Никонорова, Л. В. Бобрович // Наука и образование в ХХI веке: Материалы Междунар. науч.-практ. конф. (30 сент. 2013 г.). — Тамбов, 2013. — Ч. 18. — С. 146–148.
3. Доспехов, Б. А. Планирование полевого опыта и статистическая обработка его данных / Б. А. Доспехов. — М.: Колос, 1972. — 206 с.
4. С. В. Фролова, Л. И. Никонорова, Л. В. Бобрович, Э. Н. Аникьева. Сравнительное использование методик при обработке неполных результатов стационарного опыта // Альманах современной науки и образования. — Тамбов, 2013. — № 5 (72). — С. 177–179.
5. С. В. Фролова, Л. И. Никонорова, Л. В. Бобрович, Э. Н. Аникьева Сравнительное применение метода усреднения и метода вычеркивания при анализе данных стационарного опыта в сельскохозяйственных исследо­ваниях. Стратегия инновационного развития агропромышленного комплекса. Материалы международной научно-практической конференции 26–26 апреля 2013 г., Курган 2013. — С.- 482–486.