Инвариантность во времени распределения вероятностей значений репродуктивного возраста для внебрачных рождений
Автор: Носова Мария Геннадьевна
Рубрика: 16. Демография
Опубликовано в
Дата публикации: 18.11.2017
Статья просмотрена: 63 раза
Библиографическое описание:
Носова, М. Г. Инвариантность во времени распределения вероятностей значений репродуктивного возраста для внебрачных рождений / М. Г. Носова. — Текст : непосредственный // Проблемы и перспективы экономики и управления : материалы VI Междунар. науч. конф. (г. Санкт-Петербург, декабрь 2017 г.). — Санкт-Петербург : Свое издательство, 2017. — С. 205-208. — URL: https://moluch.ru/conf/econ/archive/263/13316/ (дата обращения: 24.04.2025).
В послевоенный период в результате вынужденной безотцовщины в России был достаточно высокий уровень внебрачной рождаемости — около 20 % по сравнению с другими развитыми странами. До середины 1980-х годов доля внебрачных рождений оставалась стабильной. Но затем она стала быстро нарастать. В период интенсивного роста в 1990–2010 гг. число внебрачных рождений в России составляла от 25 % до 30 %.
Внебрачная рождаемость за последние два десятилетия стала массовым феноменом. Следует заметить, что это связано не только с одиноким материнством, но и с супружескими парами, в которых брак по каким-то причинам не зарегистрирован. Это всеобщие очень серьезные и пока плохо понятные изменения в организации семейной жизни людей. В России, как и во всем мире, происходит смена отношения к официальному зарегистрированному браку. Как по уровню внебрачной рождаемости, так и по темпам ее роста Россия занимает серединое положение в ряду экономически развитых стран (Австрия, США, Канада, Венгрия, Румыния и т. д.).
Согласно данным [1] доля внебрачных рождений по возрасту матери в России за период 1980–2010 гг. составляет (Таблица 1).
Таблица 1
Доля внебрачных рождений по возрасту матери, 1980–2010гг.
|
Возрастной интервал |
Годы |
|||||
|
1980 |
1990 |
1995 |
2000 |
2005 |
2010 |
|
|
15–19 |
18.70 |
20.20 |
27.00 |
41.00 |
48.40 |
47.20 |
|
20–24 |
7.90 |
11.00 |
17.60 |
25.60 |
28.90 |
25.90 |
|
25–29 |
9.40 |
11.80 |
18.90 |
24.70 |
25.50 |
19.90 |
|
30–34 |
13.50 |
17.30 |
22.90 |
26.40 |
26.90 |
22.70 |
|
35–39 |
21.50 |
25.50 |
30.20 |
31.20 |
30.50 |
27.00 |
|
40–44 |
23.80 |
34.80 |
36.50 |
34.90 |
34.00 |
30.90 |
|
45–49 |
23.10 |
36.50 |
35.80 |
36.80 |
33.20 |
28.20 |
Данные Таблицы 1 дают представление о некоторых структурных характеристиках внебрачной рождаемости. Они показывают, в частности, что среди женщин наиболее интенсивно внебрачная рождаемость наблюдается в самых молодых возрастах: от 15 до 19 лет. К 20 годам доля такой рождаемости в общем числе значительно снижается, наименьшее значение наблюдается в возрасте 25–29 лет, после чего снова начинает расти.
Для применения математических методов исследования наметившихся тенденций актуальным является определение демографических инвариантов, не меняющихся с течением времени [2]. Одной из таких характеристик является распределение вероятностей значений репродуктивного возраста женщин для внебрачных рождений. Определим ее следующим образом. В демографии широко используются возрастные коэффициенты рождаемости K(x,t) — число детей рожденных за год тысячей женщин возраста (x) в году t. Определим функцию
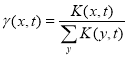 ,
,
значением которой является доля детей, рожденных в году t женщинами возраста (x), т. е. γ(x,t) — плотность распределения вероятностей значений репродуктивного возраста.
Статистические данные показывают, что возрастные коэффициенты за последние годы существенно меняются во всех возрастных группах.
Однако величины γ(x,t) обнаруживают определенную стабильность во времени. Приведем обоснование этого факта статистическим анализом возрастных коэффициентов рождаемости K(x,t) для внебрачных рождений.
Используя данные из Таблицы 1 и данные о значениях возрастных коэффициентов рождаемости [3], найдем значения возрастных коэффициентов рождаемости для внебрачных рождений. Получим следующую таблицу.
Таблица 2
Значения возрастных коэффициентов рождаемости для внебрачных рождений, 1980–2010гг.
|
Возрастной интервал |
Годы |
Сумма |
|||||
|
1980 |
1990 |
1995 |
2000 |
2005 |
2010 |
||
|
15–19 |
8.15 |
11.11 |
12.10 |
11.23 |
13.31 |
12.75 |
ν1·=68.65 |
|
20–24 |
12.45 |
17.22 |
19.84 |
23.96 |
25.09 |
22.66 |
ν2·=121.21 |
|
25–29 |
9.59 |
10.99 |
12.57 |
16.62 |
19.87 |
19.74 |
ν3·=89.37 |
|
30–34 |
7.02 |
8.34 |
6.76 |
9.29 |
12.24 |
15.28 |
ν4·=58.92 |
|
35–39 |
4.04 |
4.95 |
3.20 |
3.68 |
5.43 |
8.10 |
ν5·=29.40 |
|
40–44 |
1.10 |
1.46 |
0.80 |
0.84 |
1.02 |
1.82 |
ν6·=7.04 |
|
45–49 |
0.09 |
0.07 |
0.04 |
0.04 |
0.07 |
0.09 |
ν7·=0.39 |
|
Сумма |
ν·1=42.44 |
ν·2=54.13 |
ν·3=55.30 |
ν·4=65.68 |
ν·5=77.02 |
ν·6=80.43 |
|
Суммы по столбцам в этой таблице обозначены через ν·j. Таблица 2 представляет собой s независимых рядов наблюдений, каждому из которых соответствует один столбец. Проверим гипотезу о том, что s выборок, представленных столбцами в Таблице 2, извлечены из одной и той же совокупности, или, иначе говоря, что в этом отношении данные однородны [4]. Такая гипотеза эквивалента гипотезе о том, что существует r постоянных p1, p2,…, pr, таких, что ![]() , и вероятность принадлежности отдельного результата к i-ой группе во всех s последовательностях равна pi.
, и вероятность принадлежности отдельного результата к i-ой группе во всех s последовательностях равна pi.
Для доказательства их независимости (а следовательно однородности данных) воспользуемся критерием согласия χ2 [4, 5]. Чтобы проверить гипотезу, вычислим χ2 по формуле
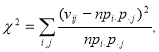
где n — объем выборки, ![]() ,
, ![]() .
.
По данным Таблицы 2 получим, что χ2=6.005. Определяя критическое значение χα2 для уровня значимости α=0.05 и m=(r-1)(s-1)=30 степеней свободы, найдем по таблице значения χα2=43.773. Поскольку χ2< χα2, то можно утверждать, что статистические данные, приведенные в таблице 2, не противоречат гипотезе об однородности данных, следовательно, эту гипотезу можно принять. Можно полагать, что γ(x,t)=γ(x).
Таким образом, показано, что распределение вероятностей репродуктивного возраста для внебрачных рождений инвариантно по времени, по крайней мере, в период 1980–2010 гг.
Этот статистический результат отражает качественную картину, заключающуюся в том, что изменения во времени коэффициентов рождаемости для внебрачных рождений связано с изменением социально-экономической ситуации в стране, а инвариантность определяется более стабильной физиологией женщины.
Согласно проведенным исследованиям [6, 7] на репродуктивное поведение женщин влияют следующие социально-экономические факторы:
‒ тип поселения (город/село): прирост рождаемости в городе был выше, чем на селе, хотя абсолютное число рождений в расчете на одну женщину на селе по-прежнему оставалось выше.
‒ состояние в браке или наличие партнера: одинаково значимы оказались не только зарегистрированный брак, но и партнер в домохозяйстве.
‒ трудовой статус партнера: его занятость увеличивает вероятность рождений.
‒ обеспеченность жильем.
‒ образование: наблюдаются сильные отличия в уровнях рождаемости у женщин с высшим образованием от прочих образовательных групп в сторону более поздних рождений и меньшего числа детей.
Общая низкая рождаемость является главной проблемой современной России [6, 7]. Она предопределяет сокращение численности населения и ведет к старению возрастного состава. Быстрое сокращение численности населения и изменение демографического баланса между поколениями имеют далеко идущие последствия для функционирования всего общества, его социальной, экономической и политической систем.
В этой сложной ситуации перед обществом стоит вопрос о том, что же необходимо и возможно сделать для устранения негативных тенденций или, по меньшей мере, ослабления их социально-экономических последствий.
Литература:
- Население России 2010–2011. Восемнадцатый — девятнадцатый ежегодный де-мографический доклад. Ответственный редактор А. Г. Вишневский. М., Изд. дом Высшей школы экономики, 2013. — 530 с.
- Носова М. Г. Применение математической модели к исследованию процесса изменения демографической ситуации в Российской Федерации // Молодой ученый. — 2017. — № 42. — С. 1–4.
- Демографический ежегодник России 2015 // Федеральная служба государственной статистики (Росстат). URL: http://www.gks.ru/wps/wcm/connect/rosstat_main/rosstat/ru/statistics/publications/catalog/doc_1137674209312 (дата обращения: 19.10.20173.
- Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся втузов. — М.: Наука, 1986. — 720 с.
- Венецкий И. Г. Статистические методы в демографии. — М.: Статистика, 1977. — 207 с.
- Носова М. Г. Автономная немарковская система массового обслуживания и ее применение в задачах демографии: Дис. … канд. физ.-мат. наук: 05.13.18/Мария Геннадьевна Носова. — Томск, 2010. — 204 с.
- Малева Т. М., Синявская О. В. Социально-экономические факторы рождаемости в России: эмпирические измерения и вызовы социальной политике // Журнал «SPERO». — 2006. — № 5. — С. 70–97.
Похожие статьи
Геометрические приложения определенного интеграла в задачах о добавочной выгоде производителя и потребителя и при нахождении коэффициента Джини
В статье рассматриваются некоторые задачи экономики, при решении которых используется нахождение площади плоской фигуры.
Похожие статьи
Геометрические приложения определенного интеграла в задачах о добавочной выгоде производителя и потребителя и при нахождении коэффициента Джини
В статье рассматриваются некоторые задачи экономики, при решении которых используется нахождение площади плоской фигуры.











