Применение вероятностных моделей многотоварных торговых операций при реализации взаимозаменяемых товаров
Авторы: Бушуева Анна Валерьевна, Пасечникова Любовь Юрьевна
Рубрика: 3. Общие вопросы экономических наук
Опубликовано в
Дата публикации: 23.09.2013
Статья просмотрена: 221 раз
Библиографическое описание:
Бушуева, А. В. Применение вероятностных моделей многотоварных торговых операций при реализации взаимозаменяемых товаров / А. В. Бушуева, Л. Ю. Пасечникова. — Текст : непосредственный // Актуальные вопросы экономики и управления : материалы II Междунар. науч. конф. (г. Москва, октябрь 2013 г.). — Т. 0. — Москва : Буки-Веди, 2013. — С. 8-10. — URL: https://moluch.ru/conf/econ/archive/91/4193/ (дата обращения: 25.04.2025).
Использование математических моделей является важным направлением совершенствования экономического анализа. Конкретизация данных или представление их в виде математической модели позволяет заранее выбрать наименее трудоёмкий путь решения, повышает эффективность анализа. На текущий момент в экономической науке имеет место широкое применение различных математических моделей, которые основаны на различных методах программирования, оптимизации, эконометрических методах, статистическом подходе. В данной работе рассмотрим модель, которая в качестве своей основы имеет методы теории вероятностей и случайных процессов.
Используемая для анализа стохастическая модель на данном этапе не обладает достаточной полнотой для описания реальных процессов, однако, достаточно адекватно отражает торговые операции по реализации нескольких товаров.
Построение подобной модели позволяет решать ряд оптимизационных задач, таких как оптимизация торгового ассортимента по распределению расходов на приобретение входящих в него товаров по их продажной цене.
Рассмотрим торговую деятельность, состоящую из некоторой последовательности сделок, выручка от каждой из которых повторно инвестируется на осуществление следующей подобной сделки в объеме, определяемом объемом полученной выручки.
Будем исследовать модель реализации товаров 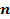 типов, образующих однородные партии по
типов, образующих однородные партии по 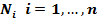 идентичных торговых единиц в каждой из партий. Закупочная оптовая цена каждой единицы товара
идентичных торговых единиц в каждой из партий. Закупочная оптовая цена каждой единицы товара 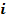 — ого типа составляет
— ого типа составляет 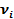 , а ее цена при первой продаже —
, а ее цена при первой продаже — 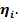 Предположим, что удельная выручка
Предположим, что удельная выручка 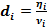 от единицы стоимости товара при каждом реинвестировании останется неизменной и равна. Получим выражение для продажной цены на втором шаге
от единицы стоимости товара при каждом реинвестировании останется неизменной и равна. Получим выражение для продажной цены на втором шаге
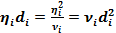 .
.
Если за фиксированный рассматриваемый промежуток времени произойдет 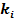 случаев закупки-продажи, то выручка от реализации единицы товара к концу интервала составит величину
случаев закупки-продажи, то выручка от реализации единицы товара к концу интервала составит величину 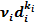 . Обозначим через
. Обозначим через 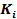 — случайную величину, которая соответствует числу спроса товара
— случайную величину, которая соответствует числу спроса товара 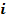 — ого типа, чьей реализацией является величина
— ого типа, чьей реализацией является величина 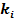 . Возьмем в качестве ее распределения пуассоновский поток случайных величин с заданными интенсивностями
. Возьмем в качестве ее распределения пуассоновский поток случайных величин с заданными интенсивностями 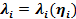 , наиболее точно описывающий данную торговую операцию. Для простоты предположим, что интенсивность
, наиболее точно описывающий данную торговую операцию. Для простоты предположим, что интенсивность 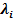 не зависит от изменений объемов и будем рассматривать интервал времени единичной длины.
не зависит от изменений объемов и будем рассматривать интервал времени единичной длины.
Необходимо оптимизировать величины продажных цен 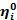 и начального ассортимента товаров. Весь ассортимент может быть определен числами единиц каждого реализуемого товара
и начального ассортимента товаров. Весь ассортимент может быть определен числами единиц каждого реализуемого товара 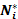 . При заданных значениях математическое ожидание общей выручки за единичный интервал времени максимизируется при ограничениях на возможный риск и имеющийся начальный капитал
. При заданных значениях математическое ожидание общей выручки за единичный интервал времени максимизируется при ограничениях на возможный риск и имеющийся начальный капитал 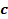 .
.
Рассмотрим случай двух товаров (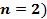 . Общая выручка составит
. Общая выручка составит 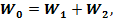 где а выручка от реализации
где а выручка от реализации 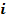 — ой типовой группы товаров будет равна
— ой типовой группы товаров будет равна
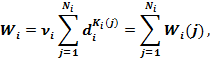
где 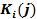 — случайное число оборотов для
— случайное число оборотов для 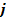 — ого экземпляра
— ого экземпляра 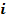 — ого типа, а
— ого типа, а 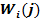 — вносимая им выручка.
— вносимая им выручка.
Найдем математическое ожидание и дисперсию случайных величин 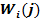 при пуассоновской аппроксимации исследуемого процесса, чтобы затем, в предположении, что достаточно велики числа
при пуассоновской аппроксимации исследуемого процесса, чтобы затем, в предположении, что достаточно велики числа 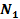 и
и 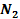 , можно воспользоваться центральной предельной теоремой:
, можно воспользоваться центральной предельной теоремой:
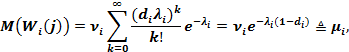
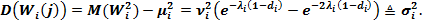
Поэтому получаем, что
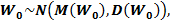
где 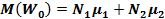 , D
, D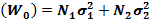 .
.
Необходимо решить задачу условной оптимизации
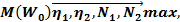
при условиях 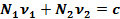 ,
, 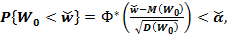 в которых
в которых 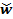 ,
, 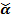 — задаваемые величины,
— задаваемые величины, 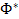 — функция Лапласа.
— функция Лапласа.
Данная модель имеет широкое применение в решении статистических и экономических задач. Рассмотрим конкретный пример оптимизации торгового ассортимента, состоящего из товаров 1-ого и 2-ого типа с закупочными ценами 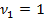 и
и 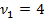 соответственно, для которых спрос аппроксимируется пуассоновскими потоками с интенсивностями
соответственно, для которых спрос аппроксимируется пуассоновскими потоками с интенсивностями
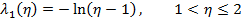
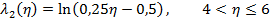
Нетрудно проверить, что данные интенсивности соответствуют функциям спроса (зависимости вероятности спроса на единичном интервале времени p от цены 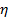 ), приведенным на рисунке:
), приведенным на рисунке:
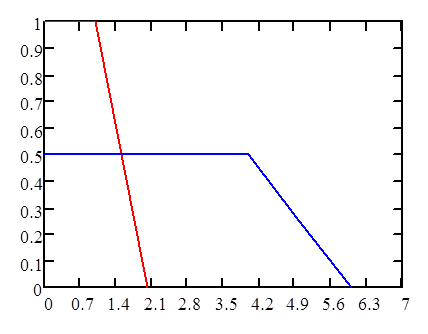
Рис. 1. Функции спроса 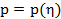
Вид получившихся функций свидетельствует о том, что товар 1-го типа ближе к товарам повседневного спроса, второй товар, в свою очередь, пользуется меньшим спросом, однако приносит большую выручку. Рынок товаров повседневного спроса, или рынок FMCG — рынок недорогих продуктов, которые быстро продаются и имеют недолгий срок службы. Несмотря на то, что абсолютная прибыль от продажи товаров на рынке FMCG невысока, общая прибыль может оказаться значительной за счет имеющихся объемов продаж. Отличительной чертой рынка FMCG можно отметить сезонность, высокую конкуренция, постоянная ротацию марок и частое возникновение новых видов товаров.
Среди товаров, которые реализуются на рынке FMCG, предметы личной гигиены, мыло, косметика, продукция для ухода за полостью рта, средства для бритья, бытовая химия, посуда, некоторые элементы питания, канцтовары. Иногда к рынку FMCG также относят и фармацевтику, бытовую электронику и ряд другой продукции.
В некоторых случаях товар второго типа может являться товаром заменителем для товара первого типа, чем, в свою очередь, и объясняется разница в поведении функций спроса для каждого из товаров. Примером взаимозаменяемых товаров могут служить молоко и сливки. Когда цена на сливки растет, потребители покупают его в меньшем количестве, что вызывает повышение спроса на молоко.
Подводя итог, стоит отметить, что когда два продукта взаимозаменяемы, между ценой на один из них и спросом на другой существует прямая зависимость. Можно привести большое количество примеров товаров данного типа: сливочное масло и маргарин, апельсины и мандарины, велосипеды и мотоциклы, куры и индейки, обувь из натуральной кожи и кожезаменителя и многие другие пары товаров.
В данном примере мы рассмотрели торговый ассортимент из товаров, в котором товаром первого типа было выбрано молоко, а товаром второго типа — сливки. Закупочные цены были взяты в пропорциональной зависимости.
Положим 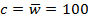 ,
, 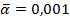 . Данный факт означает, что вероятность возврата начальных затрат к концу рассматриваемого интервала не должна быть ниже 99,9 %.
. Данный факт означает, что вероятность возврата начальных затрат к концу рассматриваемого интервала не должна быть ниже 99,9 %.
Расчёты по полученным и приведенным ранее формулам приводят к следующим оптимальным значениям продажных цен и размерам партий товаров 1-ого и 2-ого типов:
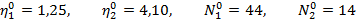
При этих данных максимально возможное значение математического ожидания общей выручки от продажи двух типов продукции составляет 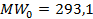 .
.
В дальнейшем может быть поставлена статистическая задача оценки влияния различных факторов на изменение величины спроса. Понятие изменения величины спроса представляет собой переход от одной комбинации «цена товара — качество товара» к другой аналогичной комбинации, при этом кривая спроса остается неизменной.
В заключении стоит отметить, что данная модель применима в различных областях коммерческой деятельности. Представляется возможным рассматривать товары различных типов и организации, ведущие коммерческую деятельность в разнообразных направлениях. Отходя от коммерческой деятельности, данная модель имеет место в решении вопросов управления инвестициями, эконометрического моделирования, финансовой математики, страховых вопросов (в частности, она может быть использована при формировании портфеля кредитных операций банка, полисов страховых фирм и. т.п.).
Литература:
1. Назаров А. А. Теория вероятностей и случайных процессов: учеб. пособие / А. А. Назаров, А. Ф. Терпугов. — Томск: Изд-во НТЛ, 2010–204с.
2. Натан А. А.. Стохастические модели в экономике: учеб. пособие. / А. А. Натан. — М.: МФТИ, 2001. — 172с.
3. Петров А. А. Опыт математического моделирования экономики / А. А. Петров, И. Г. Поспелов, А. А. Шананин — М.: Энергоатомиздат, 1996. — 544 с.
4. Макконнелл К. Р. Экономикс / К. Р. Макконнелл, С. Л. Брю — Инфа-М, 2009. — 944с.
5. Федеральная служба государственной статистики [Электронный ресурс] — URL: www.gks.ru (дата обращения: 29.08.2013).











