К вопросу о формировании знаково-символических УУД в процессе обучения решению текстовых задач

В статье рассматриваются различные приемы, направленные на формирование знаково-символических УУД в процессе решения текстовых задач. Применение знаково-символических средств позволяет адаптировать учебную информацию в доступные для учащихся формы.

Ключевые слова: универсальные учебные действия, знаково-символические УУД, схематизация, моделирование, текстовая задача.

Основным механизмом реализации целей и задач современного образования является включение учащихся разных возрастных категорий в активную учебно-познавательную деятельность. Нацеленность процесса обучения на формирование приемов умственной деятельности позволяет реализовать в практике обучения системно-деятельностный подход, базирующийся на теоретических положениях Л. С. Выготского, А. Н. Леонтьева, Д. Б. Эльконина, П. Я. Гальперина, В. В. Давыдова, А. Г. Асмолова и др. Следование этой теории позволяет сосредоточить внимание на ключевых компонентах учебной деятельности (познавательная мотивация, учебная задача, способы её решения, самоконтроль и самооценка), и создает дидактические условия для формирования универсальных учебных действий (УУД).

В стандартах второго поколения отмечается, что развитие личности в системе образования обеспечивается, прежде всего, через формирование УУД, которые являются инвариантной основой учебно-воспитательного процесса и направлены на обеспечение способности к самостоятельному усвоению новых знаний и умений, включая организацию этого процесса, а также способность субъекта к саморазвитию и самосовершенствованию путем сознательного и активного присвоения нового социального опыта.

Учебный предмет «Математика» имеет большие потенциальные возможности для формирования всех видов УУД. Реализация этих возможностей в процессе обучения математике зависит от способов организации учебно-познавательной деятельности учащихся и позволяет не только обучать математике, но и активировать способность к самостоятельному усвоению новых знаний и умений, формировать социальный статус математических знаний.

Особую группу общеучебных универсальных действий составляют знаково-символические действия: замещение; кодирование/декодирование; моделирование.

Знаково-символические универсальные действия обеспечивают конкретные способы преобразования учебного материала и выполняют следующие функции: кодирование — передача и прием информации; схематизация — использование знаково-символических средств, выполняющие функции отображения учебного материала; моделирование − выделение и отображение существенных признаков объекта с помощью оперирования знаково-символическими средствами.

Широкое использование знаково-символических средств направлено на оптимизацию процесса обучения математике. В частности, использование знаков позволяет отражать учебную информацию в более удобном и легко воспринимаемом виде. Между тем, как справедливо отмечает А. Я. Цукарь [1], знаки являются теми объектами, которые могут значительно усложнить понимание учебного материала, если оперировать ими без должной подготовки, сводя деятельность учеников к формальному заучиванию правил действий с ними без выяснения смысловой стороны знаков.

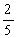Например, изучение правила нахождения числа по его дроби в учебнике «Математика 6» [2] проводится через решение следующей задачи:

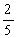Задача 1. Расчистили от снега катка, что составляет 800 м². Найдите площадь всего катка.

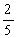
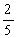
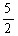
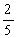Решение. Обозначим площадь катка через х м². По условию этой площади равны 800 м², т. е. х = 800. Значит х = 800: = 800 ∙ =2000. Площадь катка равна 2000 м². Далее идет формулировка самого правила, которое ученики заучивают формальным образом. Более того, образовательная практика показывает, что данное правило учащиеся часто путают с правилом нахождения дроби от числа.

При введении новых понятий, правил, процедур следует изобразить информационную составляющую носителя этой информации в виде рисунка, схемы и т. п. В данном случае, представленная ниже схема увеличивает надежность распознавания связей между данными задачи и, таким образом, достигается возможность одновременного видения этих связей.

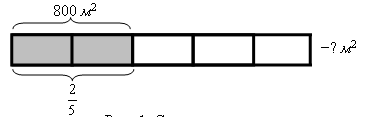
Рис. 1. Схема-рисунок задачи

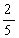Схема показывает, какие действия нужно выполнить, чтобы получить ответ на поставленный вопрос в задаче. А именно:

(800: 2) ∙ 5 = 2000 (м²), такой же результат мы получим, если 800:

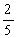После этого учащиеся приступают к самостоятельной формулировке правила. Здесь же следует привести обратную задачу: Расчистили от снега катка, площадь которого равна 2000 м². Сколько м² катка расчистили?

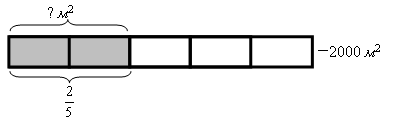
Рис. 2. Схема-рисунок обратной задачи

Приведенные выше схемы подводят учащихся к самостоятельному освоению данных правил.

Образовательная практика показывает, что многие учащиеся испытывают определенные трудности и при решении текстовых задач и «встретившись с задачей совсем не трудной, но незнакомого или малознакомого вида, не знают, как к ней подступиться, с чего начать решение» [3, с.108].

Основная причина такого положения, как отмечает Л. М. Фридман [3], состоит в том, что традиционная методика решения задач не обеспечивает формирование общих умений и способностей к решению задач.

И, как показывает наш опыт, одним из главных недостатков, возникающих при решении текстовых задач, связан с трудностями отображения информационных переходов от реальных объектов к схематизированной реальности (визуализация величин и связей между ними, представленных в задаче).

Следовательно, необходимо скорректировать методику работы по первичному восприятию и анализу задачи, которая заключается в умении так представить условие задачи в знаково-символической форме, чтобы задача стала предельно понятной для ученика. В противном случае краткая запись условия задачи не только не помогает ученику выбрать план решения, но часто приводит еще к большим затруднениям.

Качественно выполненная работа на подготовительном этапе поможет ученику свободно переключаться с восприятия одного данного на другое без потери данных и связей между ними, будет способствовать более продуктивной деятельности учащихся на следующих этапах. Дальнейшая деятельность ученика будет связана с осознанным и доказательным выбором того или иного действия в процессе решения задачи.

Задача 2. Полина и Катя собрали вместе 8400 г клюквы, причем Полина собрала на 600 г больше, чем Катя. Сколько клюквы собрала Полина и сколько − Катя?

Образовательная практика показывает, что многие учителя рекомендуют делать краткую запись условия задачи в таком виде:

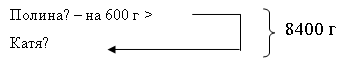
Рис. 3. Схема-рисунок условия задачи

Запись условия задачи в таком виде не соответствует адекватному восприятию учащимися задачной ситуации и не способствует созданию образа, необходимого для фиксации связей между величинами. Такой способ представления информации может привести к случайной манипуляции с числовыми данными в процессе решения задачи.

Следовательно, необходим выбор такого способа отражения задачной ситуации, который бы наглядно показывал не только скрытые зависимости между величинами, но и побуждал учащихся активно мыслить и искать наиболее рациональные пути решения задачи. В нашем случае задачную ситуацию следует представить в виде схемы:

Рис. 4. Схема-рисунок условия задачи

По схеме видно, что если от общего количества клюквы вычесть 600 г, то получится удвоенное количество клюквы, которую собрала Катя. Следовательно, Катя собрала: (8400–600): 2 = 3900 (г). Или, добавив к общему количеству 600 г, мы получим удвоенное количество клюквы, которую собрала Полина. То есть, Полина собрала: (8400 + 600): 2= 4500 (г).

Данная схема позволяет легко перейти и к алгебраическому способу решения. Для этого необходимо ввести переменную и выразить через нее неизвестные величины и составить модель задачной ситуации. Поскольку девочки собирали клюкву вместе, то образ модели будет выглядеть так:

П (г) + К (г) = 8400 (г). Схема подсказывает, как вводить переменную. Очевидно, что: x (г) собрала Катя.

(x + 600) (г) собрала Полина.

Составим уравнение: (x + 600) + x = 8400. Решение данного уравнения не представляет трудностей для учащихся 5 классов.

Задача 3. В первый день турист прошел 38 км, во второй — на 13 км меньше, а в третий день на 9 км больше, чем за второй день. Сколько километров прошел турист за три дня?

Как показывает образовательная практика, при составлении схемы задачи величины желательно изображать в виде прямоугольников с соблюдением определенного масштаба. Предложенная схема позволяет решить задачу с помощью последовательности действий или составлением числового выражения, предварительно создав его образ.

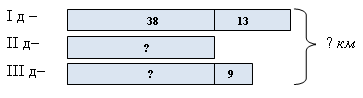
Рис. 5. Схема-рисунок условия задачи

1) Сколько километров прошел турист за II день?

38–13 = 25 (км).

2) Сколько километров прошел турист за III день?

25 + 9 = 34 (км).

3) Сколько километров прошел турист за три дня?

38 +25 + 34 = 97 (км).

Схема показывает, как нужно составить числовое выражение для получения ответа:

I (км) + II (км) + III (км), где I (км), II (км), III (км) — длины путей, проходимые туристом соответственно за каждый день.

Составим числовое выражение: 38 + (38–13) + (38–13 + 9) = 97.

Задача 4. В двух мотках 72 м веревки. В первом мотке в 3 раза меньше веревки, чем во втором. Сколько метров веревки в каждом мотке?

Для данной задачи следует применить схему, которая более адекватна условию и точнее выражает связь между данными.

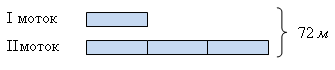
Рис. 6. Схема-рисунок условия задачи

С помощью такой схемы можно легко решить задачу арифметическим или алгебраическим способом.

В процессе составления и решения задач могут быть использованы различные знаково-символические средства для представления информационной структуры задачи:

-                     графической модели — рисунок, условный рисунок, чертеж, график, схема и вопрос;

-                     знаковой модели — краткая запись задачи, таблица;

-                     знаковой модели, представленной математическим языком — выражение, уравнение, запись решения задачи по действиям;

-                     словесно-знаковой модели и др.

Чаще всего текстовые сюжетные задачи решают арифметическим или алгебраическим способом. Иногда полезно решать задачи на основе графических или геометрических моделей, используя графические и геометрические построения. Такие разносторонние способы решения задач способствуют развитию вариативного мышления. В дальнейшем учащиеся сами определят, какому способу нужно отдать предпочтение.

Задача 5. Два снегохода вышли одновременно навстречу друг другу из двух пунктов А и В, расстояние между которыми 275 км. Через сколько часов они встретятся, если скорость одного 25 км/ч, а скорость другого на 5 км/ч больше?

Решение.

1-й способ. В прямоугольной системе координат по горизонтали отложим время движения (в часах), по вертикали — расстояние (в километрах).

Примем длину одного отрезка по вертикали за 25 км, а длину одного отрезка по горизонтали — за 1 ч. Построим графики, характеризующие движение каждого снегохода. Движение первого снегохода определяется функцией y = 25х, второго — у = 275 − 30х. Абсцисса точки пересечения их графиков (точка О) указывает, через сколько часов снегоходы встретятся. Из чертежа видно, что ее значение равно 5. Ордината указывает, на каком расстоянии от пункта А произойдет встреча. Ее значение равно 125 (рис. 7).

2-й способ. Пусть время движения снегоходов до встречи изображается отрезком ОТ, а скорость сближения — отрезком OS. Тогда площадь S прямоугольника OРRT соответствует расстоянию между пунктами А и В. Учитывая, что снегоходы сближаются каждый час на 25 + 30 = 55 (км) — сторона OР прямоугольника OРRT, расстояние между пунктами равно 275 км, имеем уравнение 275 = 55 ∙ ОТ, т. е. нужно найти сторону OT. Решив уравнение, находим ОТ = 5 (ч). Итак, снегоходы встретятся через 5 ч (рис. 8).

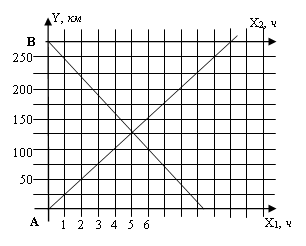
Рис. 7. Схема-рисунок решения задачи

Рис. 8. Схема-рисунок решения задачи

Применение схематизации в процессе решения текстовых задач как способа подачи информации позволяет активно и целенаправленно формировать умение оперировать знаково-символическими средствами, развивать образный компонент мыслительной деятельности учащихся. В конечном итоге, организация и осуществление этой деятельности направлены на реализацию их образовательного потенциала.

Литература:

1.      Цукарь А. Я. Методические основы обучения математике в средней школе с использованием образного мышления: Дис… д — ра пед. наук: 13. 00. 02. — М.: РГБ, 2003. — 430.

2.      Математика: Учеб. Для 6 кл. общеобразоват. учреждений/ Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 9-е изд. — М.: Мнемозина, 2001. — 304 с.: ил.

3.      Фридман Л. М. Теоретические основы методики обучения математике: Учебное пособие. Изд. 2-е, испр. и доп. — М.: Едиториал УРСС, 2005. − 248 с.