Роль и содержание курса «Математическая логика» в формировании общекультурных и профессиональных компетенций бакалавров по направлению подготовки «Математика и компьютерные науки»
Автор: Шарафеева Ландыш Рамилевна
Рубрика: 9. Педагогика высшей профессиональной школы
Опубликовано в
VI международная научная конференция «Актуальные вопросы современной педагогики» (Уфа, март 2015)
Дата публикации: 13.02.2015
Статья просмотрена: 490 раз
Библиографическое описание:
Шарафеева, Л. Р. Роль и содержание курса «Математическая логика» в формировании общекультурных и профессиональных компетенций бакалавров по направлению подготовки «Математика и компьютерные науки» / Л. Р. Шарафеева. — Текст : непосредственный // Актуальные вопросы современной педагогики : материалы VI Междунар. науч. конф. (г. Уфа, март 2015 г.). — Уфа : Лето, 2015. — С. 247-250. — URL: https://moluch.ru/conf/ped/archive/148/7367/ (дата обращения: 29.04.2025).
В современной системе высшего образования продолжается этап модернизации, суть которой заключается в принятии стандартов нового поколения. Необходимость в новых Федеральных государственных образовательных стандартах (ФГОС) третьего поколения связано с тем, что современному обществу необходимы выпускники вузов адаптированные к реальным условиям деятельности предприятий и организаций. В предыдущих стандартах было конкретно указано название и количество учебных курсов, их содержание и структура, т. е. ФГОС и учебные планы были нечетко ориентированы на требуемые профили подготовки специалистов. Стандарты нового поколения ориентированы на результат учебного процесса, другими словами в ФГОС 3+ говорится о том, какими компетенциями должен обладать выпускник вуза. Компетентностный подход в вузе требует от руководства составления перечня необходимых дисциплин для формирования компетенций и от преподавателей определения содержания учебных курсов.
В настоящее время достаточно изучены понятия «компетенция», «компетентность», а также вопросы формирования профессиональной компетентности на общем психолого-педагогическом уровне, но недостаточно изучены вопросы определения содержания конкретных предметов по новому ФГОС 3+ на основе компетентностного подхода.
Именно поэтому, в данной статье попробуем разработать модель определения содержания курса «Математическая логика» у бакалавров по направлению подготовки «Математика и компьютерные науки». Для достижения данной цели нам необходимо решить следующие задачи: 1) рассмотреть место математической логики в системе наук и изучить вопрос необходимости изучения математической логики бакалаврам по направлению подготовки «Математика и компьютерные науки»; 2) выявить компетенции из ФГОС 3+, формируемые в рамках данной дисциплины; 3) определить содержание курса.
1) Рассмотрим место математической логики в системе наук.
Математическая логика начала формироваться давно. Зарождение математической логики тесно связана с логикой и обязана ей своим возникновением. Основы логики, науки о законах и формах человеческого мышления, были заложены величайшим древнегреческим философом Аристотелем, который в своих трактатах обстоятельно исследовал терминологию логики, подробно разобрал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления, в том числе законы противоречия и исключения третьего. Вклад Аристотеля в логику весьма велик, недаром другое ее название — Аристотелева логика.
Современная логика связана с применением в традиционной логике математических методов, поэтому и называется математической логикой. Математическая логика изучает такие фундаментальные понятия как «аксиома», «формула», «доказательство», «теорема», а также вопросы построения математических теорий.
В то же время быстрое развитие информационных технологий способствует расширению как круга задач, решаемых с помощью математической логики, так и методов, применяемых для их решения. Это в первую очередь относится к задачам искусственного интеллекта, решение которых немыслимо без привлечения методов математической логики.
В ФГОС 3+ [1] указана область профессиональной деятельности бакалавров по направлению подготовки «Математика и компьютерные науки». Как видим, выпускник должен ориентироваться как в области математики, так и в информатики. А математическая логика реализует взаимосвязь между этими дисциплинами.
Таким образом, знание основ математической логики совершенно необходимо бакалаврам по направлению подготовки «Математика и компьютерные науки».
Итак, главной целью математической логики следует считать изучение бакалаврами основ математической логики, а также приобретение необходимых навыков решения практических задач.
2) Перечислим компетенции из ФГОС 3+, которые на наш взгляд необходимо развивать в рамках курса «Математическая логика»:
Общекультурные компетенции:
- способность к самоорганизации и к самообразованию (ОК-7).
Общепрофессиональные компетенции:
- готовность использовать фундаментальные знания в области математического анализа, комплексного и функционального анализа, алгебры, аналитической геометрии, дифференциальной геометрии и топологии, дифференциальных уравнений, дискретной математики и математической логики, теории вероятностей, математической статистики и случайных процессов, численных методов, теоретической механики в будущей профессиональной деятельности (ОПК-1).
Научно-исследовательская деятельность:
- способность строго доказать утверждение, сформулировать результат, увидеть следствия полученного результата (ПК-3).
3. Нами определена необходимость и цель изучения математической логики бакалаврами по направлению подготовки «Математика и компьютерное моделирование». Курс «Математическая логика» имеет обширное содержание. Поэтому необходимо определить содержание курса. Нами построена Модель определения содержания курса «Математическая логика» при компетентностном подходе (рис. 1).
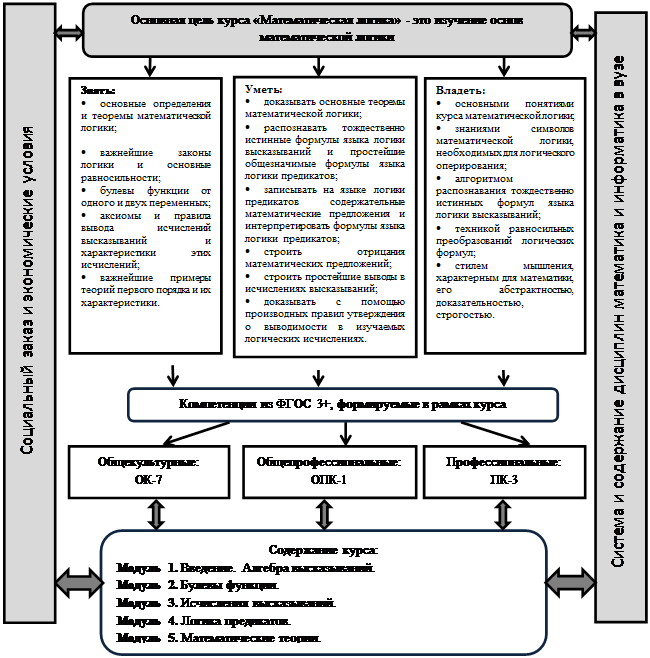 |
Рис. 1. Модель определения содержания курса «Математическая логика» при компетентностном подходе
Подробнее рассмотрим изучаемые вопросы каждого модуля и средства контроля, реализуемые при подготовке бакалавров по направлению подготовки «Математика и компьютерное моделирование» в Елабужском институте КФУ.
Модуль 1. Введение. Алгебра высказываний.
Предмет математической логики, её роль в вопросах обоснования математики. История развития математической логики. Логика высказываний. Высказывания и операции над ними. Классификация формул алгебры высказываний. Тавтологии. Основные законы логики высказываний. Равносильные формулы. Равносильные преобразования формул. Нормальные формы. СДНФ. СКНФ. Логическое следование. Приложение алгебры высказываний к логико-математической практике.
Изучение этих вопросов осуществляется во время лекционных и практических занятий. Промежуточным контролем по результатам практических занятий является контрольная работа, а лекционных — тестирование. Формируемые компетенции: ОК-7, ОПК-1, ПК-3.
Модуль 2. Булевы функции.
Булевы функции от одной переменной. Булевы функции от двух переменных. Системы булевых функций. Специальные классы булевых функций. Теорема Поста (о полноте системы булевых функций). Приложение булевых функций к анализу и синтезу релейно-контактных схем.
Изучение этих вопросов осуществляется во время лекционных и практических занятий. Промежуточным контролем по результатам практических занятий является контрольная работа, а лекционных — тестирование. Формируемые компетенции: ОК-7, ОПК-1, ПК-3.
Модуль 3. Исчисление высказываний.
Аксиоматическое построение логики высказываний. Аксиомы, правила вывода. Понятие вывода в исчислении. Выводимость из гипотез. Доказуемость формул. Производные правила. Теорема дедукции. Непротиворечивость, полнота и разрешимость исчисления высказываний. Независимость аксиом.
Изучение этих вопросов осуществляется во время лекционных занятий с демонстраций множества примеров (доказательств формул, построения вывода, применение теоремы дедукции). Промежуточным контролем является тестирование. Формируемые компетенции: ОК-7, ОПК-1, ПК-3.
Модуль 4. Логика предикатов.
Понятие предиката. Кванторы общности и существования. Формулы логики предикатов. Свободные и связные переменные. Истинностные значения формул. Равносильность. Основные равносильности. Равносильные преобразования формул. Приведенная нормальная форма. Предваренная нормальная форма. Применение языка логики предикатов для записи математических предложений, определений, построение отрицаний предложений.
Изучение этих вопросов осуществляется во время лекционных и практических занятий. Промежуточным контролем по результатам практических занятий является контрольная работа, а лекционных — тестирование. Формируемые компетенции: ОК-7, ОПК-1, ПК-3.
Модуль 5. Математические теории.
Язык первого порядка. Термы и формулы. Логические и специальные аксиомы. Правила вывода теории. Примеры математических теорий из алгебры, анализа, геометрии. Интерпретации и модели аксиоматической теории. Свойства аксиоматических теорий. Формальные теории. Теоремы Гёделя о неполноте арифметики.
Изучение этих вопросов осуществляется во время лекционных занятий с приведением множества примеров. Промежуточный контроль — тестирование. Формируемые компетенции: ОК-7, ОПК-1.
Итоговый контроль по курсу — зачет, проводится по билетам.
Для реализации учебного процесса необходимо обеспечить обучающихся учебно-методическим материалом, на этом делается акцент и в проекте ФГОС 3+. В Елабужском институте КФУ студенты обеспечены индивидуальным неограниченным доступом к электронно-библиотечным системам (znanium, bibliorossica, e.lanbook). Автором в настоящее время разрабатывается дистанционный курс в системе Moodle (http://tulpar.kfu.ru/course/view.php?id=2338), издано учебное пособие [3], содержащий конспекты лекций. Все эти возможности, во-первых, позволяют студентам проектировать свою персональную траекторию изучения дисциплины, во-вторых, развивают способность к самоорганизации и к самообразованию (ОК-7).
В системе высшего образования активно внедряется ФГОС 3+, где одно из важнейших позиций занимает компетентностный подход. В связи с этим необходимо особую роль выделить содержаниям учебных дисциплин. Разработанная нами модель определения курса «Математическая логика» дает возможность проследить процесс определения содержания любой дисциплины вуза.
Литература:
1. Проекты ФГОС 3+. Бакалавриат. 02.03.01 Математика и компьютерные науки. — Режим доступа: http://kpfu.ru/umu/normativnoe-obespechenie/obrazovatelnye-standarty/proekty-fgos-3.
2. Соснин Н. В. Содержание обучения в компетентностный модели ВПО (К освоению ФГОС ВПО): монография/ Н. В. Соснин. — Красноярск: Сибирский федеральный ун-т, 2011. — 242 с. — Режим доступа: http://znanium.com/bookread.php?book=443125.
3. Шарафеева Л. Р. Математическая логика. Учебное пособие. Конспект лекций/ Л. Р. Шарафеева. — Елабуга: Изд-во ЕИ КФУ, 2014. — 124 с.











