Развитие логического мышления у учащихся с ограниченными возможностями здоровья в процессе решения задач по схемам

У детей с ограниченными возможностями здоровья обнаруживается недостаточность всех уровней мыслительной деятельности. Учащиеся затрудняются в понимании и запоминании словесно сформулированного условия задачи, воспринимают его фрагментарно, на основе отдельных слов и выражений, не понимают ситуации, описываемой в тексте задачи, не представляют результатов её изменения, не могут перейти от понимания предметной ситуации задачи к её математическому решению. Поэтому учащихся необходимо учить определять, какими арифметическими действиями можно их решить.

Трудности в решении задач у обучающихся с ограниченными возможностями здоровья связаны с недостаточным пониманием предметно-действенной ситуации, отраженной в задаче, и математических связей и отношений между числовыми данными, а также между данными и искомыми. Учащиеся справляются с решением задач, если они составлены на основе действий с реальными предметами. Основные трудности возникают тогда, когда необходимо наглядно представить словесно сформированные задачи. [1,с.345].

Наглядность, особенно графическая, нужна на всём протяжении обучения как важное средство развития более сложных форм конкретного мышления и формирования математических понятий. Рисунки, схемы, чертежи помогают учащимся в сознательном выявлении скрытых зависимостей между величинами. Побуждают активно мыслить, искать наиболее рациональные пути решения задач, помогают усваивать знания и применять их.

Рассмотрим работу над задачей из учебника математики 5 класса на с. 56 № 123.

«В саду посадили 500 яблонь, вишен на 300 деревьев меньше, чем яблонь, а слив на 100 деревьев больше, чем вишен. Сколько всего деревьев посадили в саду?»

Учащиеся не смогли сразу ответить на вопрос о сливах «Сколько слив посадили?» Они отвечали: «Слив — 100 деревьев». Пришлось несколько раз перечитать условие задачи, но и тогда они ответили: «Слив на 100 меньше».

Понимание задачи, анализ ее условия происходит только тогда, когда учитель предлагает учащимся вопросы, направленные на установление логических отношений между величинами. В качестве методического приема, помогающего учащемуся установить взаимосвязь данных задачи и выработать общую схему решения, рекомендуется краткая запись условия. Опыт работы в специальной (коррекционной) школе показывает, что составление краткой записи условия задачипредставляет для учащихся большую сложность. Это умение формируется у детей постепенно, по мере обучения и продвижения в общем развитии.

Например, такая запись условия задачи трудна учащимся и для осмысления ее содержания, если она представлена в готовом виде, и для самостоятельного ее составления:

Яблони — 500 д.

Вишни — на 300 д. меньше, чем яблонь

Сливы — на 100 д. больше, чем вишен.

Кроме того, ученикам необходимо наглядно представить соотношения величин, о которых говорится в задаче, а краткая запись в этом плане дает немного. В процессе работы пришла к мысли, что решать задачи легче с помощью какой — либо модели, конкретно, с помощью схемы. Графическая схема наглядна, она отражает в зрительной форме количественные сравнительные характеристики данных задачи (больше, меньше, равно). Она в какой-то мере конкретна, так как величины, числовые данные с ее помощью перестают быть только знаками, а становятся образами (квадратами, прямоугольниками).

В своей практике применила следующий порядок выполнения графической схемы условия задачи. Геометрические фигуры (в нашем обучении это были прямоугольники одинаковой высоты) изображали числа. Если вместо числа в геометрическую фигуру вписывалось словесное математическое выражение, это значило, что число неизвестно и, чтобы его определить, необходимо подобрать арифметическое действие, соответствующее математическому выражению. Стрелка указывала, над каким числом надо произвести действие.

Графическая схема изложенного выше условия задачи имела следующий вид:

 

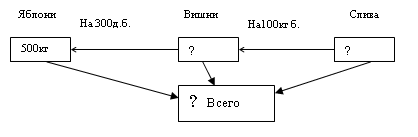
Поиск возможностей применения графического моделирования задачи привело к мысли использовать схему в виде рисунка. Она проста в исполнении, посильна для любого ребёнка, наглядна и, кроме этого, вызывает положительные эмоции. Схема удовлетворяет требованиям задачи: отображает количественные соотношения, предлагаемые в задаче; показывает связи между данными и искомыми, что позволяет легко сориентироваться в выборе действия. Объясняя свои действия при составлении схемы, ученик постоянно привыкает описывать ход мысли словами, что является базой для формирования умения анализировать задачу.

Постепенный переход от использования предметной наглядности к использованию схемы способствует формированию умения абстрагироваться — умения, необходимого для развития мышления.

Используемая схема состоит из элементов, смысл которых легко понимают дети. Схема ими легко выполняется, так как не требует никаких специальных графических умений, но требует умения писать опорные слова, что необходимо для оформления краткой записи. Схема является абстрактным изображением ситуации, которая дана в задаче, она позволяет отклониться от несущественных подробностей, приучает быстро находить главное в задаче — данные, искомое и помогает осознать условие, и выбрать действие.

Но это является конечным результатом работы. Для устранения списывания готового решения необходимо улучшить организацию первичного восприятия и анализа задачи, для осознанного выбора арифметического действия всеми учащимися. Главное на этом этапе — понять задачу, то есть уяснить, о чём эта задача, что в ней известно, что нужно узнать, как связаны между собой данные, каковы соотношения между данными и искомыми. Для этого с ребятами разбираем текст на смысловые части и моделируем их. Моделирование — замещение изучаемого объекта другим, специально созданным в упрощенно-обобщенном виде, использование моделей в процессе обучения способствует развитию у учащихся высшей формы наглядно — образного мышления — наглядно — схематического. [2, с. 145] При таком подходе в обучении решению задач выбор действия будет понятным и обоснованным, учащиеся не будут действовать наугад, механически манипулируя числами. Составленная математическая модель задачи (а это наглядный рисунок — схема) показывает им главные связи между данными искомыми и отражает количественные соотношения.

При обучении использованию схемы в моделировании простых и сложных задач на этапе ознакомления используются следующие приемы.

1.      Разъяснение учителем каждой модели.

2.      Указание к построению модели.

Сначала необходимо выбрать слова, характеризующие предметы, о которых говорится в задаче. Затем определить, какое слово включает общее понятие, какие слова являются частями целого.

3.      Моделирование по наводящим вопросам учителя и поэтапное выполнение схемы:

-        учителем на доске;

-        учащимися на доске;

-        одновременно учителем на доске, учащимися в тетради.

На этапе осмысления схематического чертежа можно использовать следующие приемы:

1.    Формулирование текста задачи по предложенному сюжету и схематическому чертежу.

2.    По схеме объяснить, что обозначают данные выражения.

3.    Предлагается модель. Необходимо указать на схеме количественные характеристики объектов:

-        точное указание модели;

-        выбор модели из числа предложенных.

4. Изменение модели или количественных характеристик.

5. Дополнение к построению схемы. Предлагается часть схемы, ученик достраивает его до завершения.

Вспомогательные модели одинаковые. Сюжеты задач разные. Рассуждения и решения идентичны.

Учащиеся подсказали учителю, что главный вопрос задачи изображался на чертеже самым большим знаком вопроса (он самый последний, самый важный). Таким образом, взглянув на чертеж, каждый мог видеть порядок действий в решении задачи.

К концу I четверти учащиеся могли уже, еще не выполняя чертежа, представить его себе и сравнить с предыдущим чертежом. Потом устно разбирая его особенности, ученики выполняли чертеж самостоятельно. В дальнейшем же дети только устанавливали особенности чертежа, его отличие от выполненного ранее. Когда учащимся стали известны все варианты данной задачи, перешли к новой, несколько отличающейся от изученной.

Графическая наглядность нужна на протяжении обучения как важное средство развития логического мышления и формирования математических понятий.

Даже простые задачи стараемся решать с помощью графического моделирования. Такой рисунок прост в исполнении, нагляден, дети с удовольствием составляют схемы. Главное достоинство схемы — это точное отображение смысла операций сложения (объединение) и вычитания (удаления части). Объясняя свои действия при составлении схемы, ученик привыкает описывать ход мысли словами. Переход к использованию схемы способствует формированию умения абстрагироваться — умения, являющегося необходимым для развития логического мышления. [3, с. 127]Схема легко выполняется любым учеником.

Схема несет двоякую нагрузку: с одной стороны, она является абстрактной моделью задачи, с другой — схема достаточно конкретна. Она воплощает те мыслительные действия, которые ученик проделывает, моделируя задачу.

Наличие схемы на стенде помогает даже слабому ученику. Аналитический подход к задаче способствует развитию логического мышления, сокращает время решения. Готовая схема — схема решения. Схема — это также и средство контроля (самоконтроля), поскольку ученик всегда может сравнить выполняемые им действия со способом действия, зафиксированным в схеме.

Образцы схем к задачам.

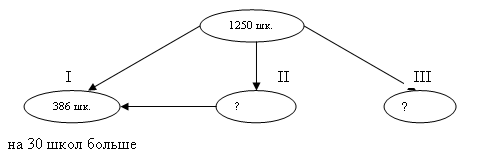
В трех летних трудовых лагерях работало 1250 школьников. В одном лагере было 386 человек, в другом на 30 человек больше. Сколько школьников в третьем лагере?

 

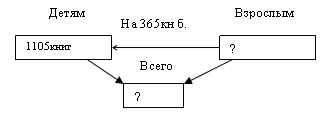
В библиотеке 1105 книг для детей, а для взрослых на 365 больше. Сколько всего книг в библиотеке?

 

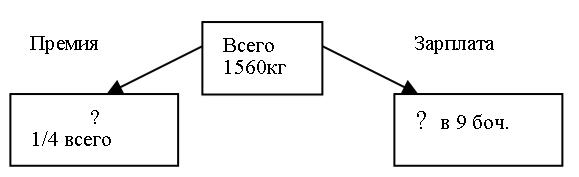
Заготовили 1560 кг капусты. Четвертую часть всей капусты оставили свежей, а остальную засолили в девяти бочках поровну. Сколько кг капусты в каждой бочке?

 

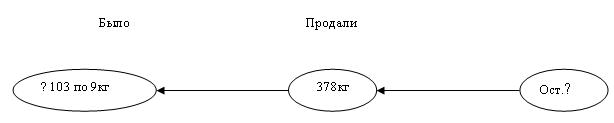
В магазин поступило 103 ящика с яблоками, по 9 кг в каждом. Продали 378 кг. Сколько кг яблок осталось?

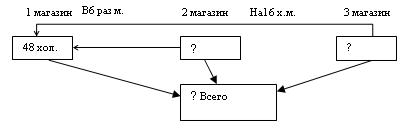
В первый магазин привезли 48 холодильников, во второй в 6 раз меньше, а в третий на 16 холодильников меньше, чем в первый магазин. Сколько всего холодильников привезли в три магазина?

 

На уроках математики учащиеся учатся применять теоретические знания, вычислительные и измерительные умения и навыки при решении задач. В арифметических задачах используется числовой материал из жизни нашей страны. Это способствует расширению кругозора учащихся, обогащению их новыми знаниями об окружающей действительности, заставляя учащихся самих «добывать» числовой материал для составления задач.Задачи ставит жизнь, и уметь их решать, значит подготовить себя к социальной адаптации в условиях современного мира. [1,с.12].

 

Литература:

 

1.                  Перова, М. Н. Методика преподавания математики в коррекционной школе VIII вида [Текст] / М. Н. Перова.— М.: Гуманит. изд. центр ВЛАДОС, 2001. — 408 с.

2.                  Обучение детей с нарушениями интеллектуального развития (Олигофренопедагогика) [Текст] / под редакцией Б. П. Пузанова. — М.: Изд. центр «Академия», 2008. — 269 с.

3.                  Липа, В. А. Основы коррекционной педагогики [Текст] / В. А. Липа— Донецк: «Лебедь», 2002. — 327 с.