Применение современных компьютерных технологий при прогнозировании методом статистического анализа

Прогнозирование, основанное на использовании методов статистического анализа ретроспективных данных, допустимо в том случае, когда между прошлым и будущим имеется определенная причинно-следственная связь.

Алгоритм построения прогноза методом статистического анализа состоит из следующих шагов:

— строится график зависимости спроса от времени, используя Мастер диаграмм Excel.

Порядок построения следующий:

1)       введите исходные данные или откройте существующий файл, содержащий анализируемые данные;

2)       активизируйте Мастер диаграмм любым из следующих способов:

а)      в главном меню выберите Вставка/Диаграмма;

б)      на панели инструментов Стандартная щелкните по кнопке Мастер диаграмм;

3)       в окне Тип выберите График (рис.1) вид графика выберите в поле рядом со списком типов. Щелкните по кнопке Далее;

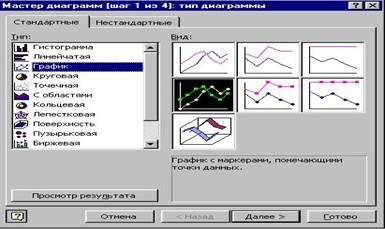
Рис. 1. Диалоговое окно Мастера диаграмм: тип диаграммы

4)       заполните диапазон данных, как показано на рис. 2. Установите флажок размещения данных в столбцах (строках). Щелкните по кнопке Далее;

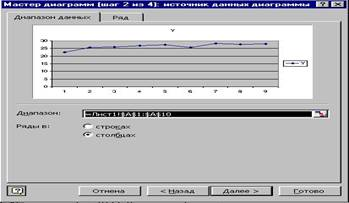
Рис. 2. Диалоговое окно Мастера диаграмм: источник данных

5)       заполните параметры диаграммы на разных закладках (рис3.): название диаграммы и осей, значения осей, линии сетки, параметры легенды, таблица и подписи данных. Щелкните по кнопке Далее;

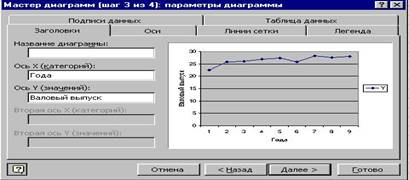
Рис. 3. Диалоговое окно Мастера диаграмм: параметры диаграммы

6)  укажите место размещения диаграммы на отдельном или на имеющемся листе (рис.4). Щелкните по кнопке Далее. Готовая диаграмма выведется на указанное место;

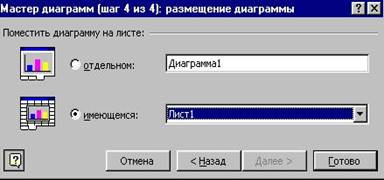
Рис. 4. Диалоговое окно Мастера диаграмм: размещение диаграммы

-        на основе визуального изучения графика делается предположение об аналитической форме кривой, которая наилучшим образом способна аппроксимировать ломаную на графике;

-        применяется метод наименьших квадратов для построения прогнозирующей кривой;

-        оценивается среднее значение погрешности полученных прогнозных оценок;

-        принимается решение об использовании или не использовании выбранной кривой для построения прогноза.

Наиболее часто употребимым методом построения прогнозирующей функции является метод наименьших квадратов.

Метод наименьших квадратов позволяет подобрать некоторую непрерывную аналитическую функцию для аппроксимации дискретного набора исходных данных. Выбор функции считается наилучшим, если сведено к минимуму стандартное отклонение по рассматриваемой временной выборке, которое определяется по формуле:

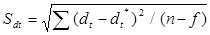                                                                                  (1)

где: d_t — фактический спрос, наблюдаемый в t-й период (отрезок) времени;

d_t* — значение прогнозирующей функции для того же момента времени;

п — число периодов (наблюдений), т. е. длина временной выборки;

f — число степеней свободы.

Суммирование ведется по всей выборке, поэтому, как это принято в статистике, нижний и верхний индексы суммирования опущены.

Минимизация S_dt эквивалентна минимизации Σ(d_t — d_t*)². Поэтому задача сводится к минимизации суммы квадратов разностей между фактическим значением спроса в момент t и тем значением, которое принимает прогнозирующая функция.

Наиболее часто для построения прогнозирующей функции используют линейную функцию у = а₀ + a₁t,

параболу у = а₀ + a₁t + a₂t ²,

гиперболу у = а₀ + a₁ / t,

многочлены более высоких порядков.

Если предположить, что выбрана линейная форма прогнозирующей функции, то есть у = а₀ + a₁t, то для определения исходно неизвестных параметров а₀ и а₁ необходимо минимизировать 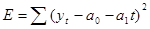. Для этого определяют первые частные производные Е по а₀ и а₁ и приравнивают их нулю, т. е. решают следующую систему уравнений:

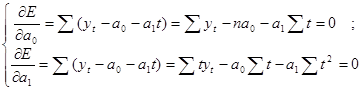                                            (2)

откуда и получают искомые значения параметров а₀ и а₁.

Аналогично получают параметры для гиперболы и параболы.

Поведение спроса часто носит циклический (периодический) характер. Тогда прогнозирующая функция может быть представлена в виде:

у == а + u cos(2π / N) t + v sin(2π / N) t,                                                                       (3)

где N — число периодов в одном цикле.

Суперпозиция линейной и циклической функций позволяет получить линейно-циклическую функцию:

у = а + bt + u cos(2π / N) t + v sin(2π / N) t,                                                                  (4)

Определение фигурирующих в формулах констант осуществляется методом наименьших квадратов.

Таким образом, необходимо помнить, что при выборе прогнозирующей функции предпочтение отдается той аналитической форме, которая обеспечивает минимальное из стандартных отклонений как погрешность оценки аппроксимации. Поэтому если нет уверенности, что тот или иной вид прогнозирующей функции заведомо предпочтительнее других, то следует испытать несколько различных форм прогнозирующей функции и выбрать наилучшую в соответствии с критерием минимизации стандартного отклонения.

Литература:

1.                  Мирзоева Е. В. Математические методы и модели в экономике: Учебник / Е. В. Мирзоева, С. Н. Грицюк, В. В. Лысенко — Ростов н/Д: Феникс, 2007- 348 с.