Интерактивная технология (метод проектов) как один из видов инновационных технологий на уроках математики и во внеурочное время

 

Новые стандарты ФГОС включают в себя не только требования к знаниям, но и к уровню воспитанности, к уровню развития личности, а также к условиям образования. Вот почему перед преподавателями остро встала и в настоящее время остаётся актуальной проблема самостоятельного успешного усвоения обучающимися новых знаний, умений и компетенций, включая умение учиться; выпускать в жизнь человека обучаемого, способного самостоятельно учиться и готового к самостоятельным действиям и принятию решений.

«Скажи мне — и я забуду. Покажи мне — и я запомню. Дай мне действовать самому — и я научусь». Эти слова мудрого Конфуция современны как никогда. Конечно, быстрее и легче показать, объяснить, чем позволить обучающимся самим открывать знания и способы действий. Самостоятельно ставить цели, анализировать, сопоставлять, оценивать, а главное — не бояться ошибаться в поисках нового пути.

В российском образовании сегодня действует принцип вариативности, который даёт педагогическим коллективам конструировать педагогическийпроцесс, используя авторские разработки. В этих условиях преподавателю необходимо не только ориентироваться в широком спектре инновационных технологий, идей, направлений, но и, тщательно изучив их, не открывая уже открытое, применять их на практике.

Традиционные способы обучения постепенно сдают свои позиции, так как нужны специалисты, владеющие не только знаниями, но и умениями, навыками самостоятельно добывать их.

«Если мы учим сегодня так, как учили вчера, мы крадём у наших детей завтра». Ю. Дьюи.

Следовательно, старая парадигма образования — «учитель — учебник — ученик» — должна быть заменена на новую — «ученик — учебник — учитель».

А задача учителя состоять в организации эффективной учебной деятельности учащихся, в обучении их самостоятельно добывать дополнительные знания для успешного освоения предметом.

Понятие «инновация» определяется как нововведение, приращение, способствующее качественному изменению образовательной среды. В качестве результата инновационной деятельности рассматривается переход системы из одного состояния в другое, обеспечивающий повышения качества образования.

Введение новых технологий вносит радикальные изменения в систему образования: ранее ее центром являлся преподаватель, а теперь — учащийся. Это дает возможность каждому ученику обучаться в подходящем для него темпе и на том уровне, который соответствует его способностям.

В последнее время в группе активных технологий обучения, где ученик наряду с учителем занимает активную позицию (если ученик работает самостоятельно — лабораторный метод, работа с книгой, документами) в процессе добывания знаний, стали выделять интерактивные технологии.

Поэтому в своей практике считаю обязательным использование метода проектов, так называемой интерактивной образовательной технологии или её элементов, как на уроках математики так и во внеурочное время.

Интерактивность (inter — взаимный, act — действовать) подразумевает взаимодействие, нахождение в режиме беседы, диалога с чем — либо (например, компьютером) или кем — либо (человеком).

Самореализация обучающихся в учебной деятельности возможна при наличии групповой работы, взаимодействии учащихся между собой, с учителем, с учебной информацией, с компьютером. Этим условиям соответствует использование в учебной деятельности интерактивных технологий, представляющих систему правил организации продуктивного взаимодействия учащихся между собой, с учителем, с компьютером, с учебной литературой, при котором происходит освоение нового опыта, получение новых знаний и предоставляется возможность для самореализации личности учащихся, выявления и раскрытия их способностей.

Другими словами, интерактивные технологии ориентированы на более широкое взаимодействие учеников не только с учителем, но и друг с другом и на доминирование активности учащихся в процессе обучения. Следовательно, использование в учебной деятельности интерактивных технологий способствует самореализации личности учащегося, повышает его мотивацию к обучению и адаптацию в образовательной среде, развивает его коммуникативные способности и ведёт к повышению внутренней самооценки.

Метод проектов позволяет отойти от авторитарности в обучении, всегда ориентирован на самостоятельную работу учащихся. С помощью этого метода учащиеся не только получают сумму тех или иных знаний, но и учатся приобретать эти знания самостоятельно, пользоваться ими для решения познавательных и практических задач.

Проект — в буквальном переводе с латинского — брошенный вперёд. Под проектом подразумевают план, предположение, предварительный текст какого — либо документа, комплекс технических документов (расчётов, чертежей, макетов, формул и т. д.)

Метод проектов — активное вовлечение учащихся в процесс поиска необходимой информации, её критического и творческого осмысления, актуализации знаний через их применение на практике.

Метод проектов всегда ориентирован на самостоятельную деятельность обучающихся — индивидуальную, парную, групповую, которую обучающиеся выполняют в течение определённого отрезка времени. Он предполагает решение какой — то проблемы, предусматривающей, с одной стороны, использование разнообразных методов, с другой — интегрирование знаний, умений из различных областей науки, техники, технологии, творческих областей.

Использование метода проектов позволяет решать следующие задачи:

                    активизация познавательной деятельности учащихся;

                    формирование у обучающихся учебной компетенции для непрерывного самообразования;

                    формирование специфических умений и навыков, а также ознакомление с методами исследования в рамках каждой образовательной области;

                    формирование общеучебных и коммуникативных навыков таких как:

• постановка учебной проблемы, формулирование темы, определение в теме объекта и предмета исследования;
• формулирование гипотезы и её положений;
• определение целей и задач проектной работы;
• выбор рационального и оптимального способа достижения цели;
• планирование самостоятельной работы;
• организация мыслительной деятельности;
• оценка результатов своих действий.

Использование проектной деятельности учащихся позволяет:

                    развивать коммуникативные и организационные навыки работы с информацией;

                    совершенствовать и тренировать мыслительную деятельность учащихся;

                    создавать устойчивые установки на активное восприятие информации;

                    стимулировать инициативу и рост творческих возможностей.

Успех человека в современном мире во многом определяется его способностью организовать свою жизнь как проект: определить дальнюю и ближайшую перспективу, найти и привлечь ресурсы, наметить план действий и, осуществив его, оценить: удалось ли достичь поставленных целей.

Многочисленные исследования, проведённые как в нашей стране, так и за рубежом, показали, что большинство современных лидеров в политике, бизнесе, искусстве, спорте — люди, обладающие проектным типом мышления.

Представлю продукт одного из проектов.

Эта работа была посвящена110-летию со дня рождения русского учёного математика А. Н. Колмогорова. Обучающимся был представлен небольшой рассказ об этом учёном, о его вкладе в отечественную науку и о его работах по изучению некоторых явлений, в том числе и о таком явлении, как турбулентность. После чего обучающимся было предложено провести исследовательскую работу.

Одна из работ, на мой взгляд, оказалась наиболее удачной. Она была представлена на общешкольной конференции и вызвала большой интерес, как среди обучающихся так и среди моих коллег учителей.

Итак, Исследовательская работа посвящена 110-летию со дня рождения русского учёного математика А. Н. Колмогорова

Тема: «Турбулентность. Просто о сложном».

Руководитель: учитель математики Крылова И. К.

Пояснительная записка

15-го марта 2013 года для учащихся 8–11-х классов в нашей школе состояласьнаучно–практическая конференция, посвящённая 110-летию со дня рождения русского учёного математика А. Н. Колмогорова.

Основной целью проведения научно-практической конференции является повышение качества образования и личностное развитие учащихся, формирование у них навыков самостоятельной учебной работы путем привлечения учащихся и педагогов к исследовательской деятельности в области математики и её практического применения.

Основные задачи конференции:

        совершенствование навыков исследовательской деятельности;

        активизация творческой и интеллектуальной инициативы учащихся;

        развитие коммуникативной компетентности учащихся, в том числе культуры публичной дискуссии;

        создание условий для успешной социальной адаптации учащихся;

        организация учебного сотрудничества и совместной деятельности с учителем и сверстниками.

Данная исследовательская работа состоит из двух частей: I часть — это доклад-выступление, II часть — презентация к докладу. Презентация создана во-первых в помощь докладчику, во-вторых для красочности и эффективности выступления, в-третьих, для максимального использования умения и навыков обучающегося, выполняющего данную исследовательскую работу.

Введение.

Андрей Николаевич Колмогоров — выдающийся русский советский математик, с 1931 года профессор Московского Государственного Университета. С 1939 — академик Академии Наук СССР.

Слайд 3

Рис. 1. Андрей Николаевич Колмогоров

 

Андрей Николаевич Колмогоров родился 12 (25) апреля 1903 г. в Тамбове. Он рано потерял родителей и был усыновлён и воспитывался сестрой матери, Верой Яковлевной Колмогоровой. Тетушки Андрея в своем доме организовали школу для детей разного возраста, которые жили поблизости, занимались с ними — десятком ребятишек — по рецептам новейшей педагогики. Для ребят издавался рукописный журнал «Весенние ласточки». В нем публиковались творческие работы учеников — рисунки, стихи, рассказы. В нем же появлялись и «научные работы» Андрея — придуманные им арифметические задачи. Здесь же мальчик опубликовал в пять лет свою первую научную работу по математике. Правда, это была всего-навсего известная алгебраическая закономерность, но ведь мальчик сам ее подметил, без посторонней помощи!

В семь лет (в 1910 году) Колмогорова определили в частную гимназию. Она была организована кружком московской прогрессивной интеллигенции и все время находилась под угрозой закрытия. Андрей уже в те годы обнаруживает замечательные математические способности, но все-таки еще рано говорить, что дальнейший путь его уже определился. Были еще увлечение историей, социологией. Одно время он мечтал стать лесничим.

«В 1918–1920 годах жизнь в Москве была нелегкой, — вспоминал Андрей Николаевич. — В школах серьезно занимались только самые настойчивые. В это время мне пришлось уехать на строительство железной дороги Казань-Екатеринбург. Одновременно с работой я продолжал заниматься самостоятельно, готовясь сдать экзамен экстерном за среднюю школу. По возвращении в Москву я испытал некоторое разочарование: удостоверение об окончании школы мне выдали, даже не потрудившись проэкзаменовать».

Когда в 1920 г. Андрей Колмогоров стал думать о поступлении в институт, перед ним возник вечный вопрос: чему себя посвятить, какому делу? Влечет его на математическое отделение университета, но есть и сомнение: здесь чистая наука, а техника — дело, пожалуй, более серьезное. Вот, допустим, металлургический факультет Менделеевского института! Настоящее мужское дело, кроме того, перспективное. Андрей решает поступать и туда и сюда. Но вскоре ему становится ясно, что чистая наука тоже очень актуальна, и он делает выбор в ее пользу.

В 1920 г. он поступил на математическое отделение Московского университета. «Задумав заниматься серьезной наукой, я, конечно, стремился учиться у лучших математиков, — вспоминал позднее ученый. — Мне посчастливилось заниматься у П. С. Урысона, П. С. Александрова, В. В. Степанова и Н. Н. Лузина, которого, по-видимому, следует считать по преимуществу моим учителем в математике. Но они «находили» меня лишь в том смысле, что оценивали приносимые мною работы. «Цель жизни» подросток или юноша должен, мне кажется, найти себе сам. Старшие могут этому лишь помочь».

В первые же месяцы Андрей сдал экзамены за курс. А как студент второго курса он получает право на «стипендию»: «...я получил право на 16 килограммов хлеба и 1 килограмм масла в месяц, что, по представлениям того времени, обозначало уже полное материальное благополучие», вспоминал учёный. Теперь есть и свободное время. Оно отдается попыткам решить уже поставленные математические задачи.

Молодой Андрей Николаевич был в восторге от лекций профессора Московского университета Николая Николаевич а Лузина, который умел зажечь молодежь желанием научного подвига, привить веру в собственные силы. Каждый студент мечтал стать гостем «Лузитании», где по знаменитым «средам» профессор со своими студентами беседовал за чашкой чая о научных проблемах. Колмогоров впервые обратил на себя внимание профессора на одной лекции. Лузин, как всегда, вел занятия, постоянно обращаясь к слушателям с вопросами, заданиями. И когда он сказал: «Давайте строить доказательство теоремы, исходя из следующего предположения…» — в аудитории поднялась рука Андрея Колмогорова: «Профессор, оно ошибочно…» За вопросом «почему» последовал краткий ответ первокурсника. Довольный Лузин кивнул: «Что ж, приходите на кружок, доложите нам свои соображения более развернуто». «Хотя мое достижение было довольно детским, оно сделало меня известным в «Лузитании», — вспоминал Андрей Николаевич.

Но лишь через год серьезные результаты, полученные восемнадцатилетним второкурсником Андреем Колмогоровым, обратили на себя настоящее внимание «патриарха». С некоторой торжественностью Николай Николаевич предлагает Колмогорову приходить в определенный день и час недели, предназначенный для учеников его курса. Подобное приглашение, по понятиям «Лузитании», следовало расценивать как присвоение почетного звания ученика. Как признание способностей.

Первая публикация Колмогорова появилась в 1923 году и была посвящены проблемам математического анализа.

Особое значение для приложения математических методов к естествознанию и практическим наукам имел закон больших чисел. Разыскать необходимые и достаточные условия, при которых он имеет место, — вот в чем заключался искомый результат. Крупнейшие математики многих стран на протяжении десятилетий безуспешно старались его получить. В 1926 году эти условия были получены аспирантом Колмогоровым.

Многие годы тесного и плодотворного сотрудничества связывали его с Александром Яковлевичем Хинчиным, который в то время начал разработку вопросов теории вероятностей. Она и стала областью совместной деятельности ученых. Наука «о случае» еще со времен Чебышева являлась как бы русской национальной наукой. Ее успехи преумножили многие советские математики, но современный вид теория вероятностей получила благодаря аксиоматизации, предложенной Андреем Николаевичем в 1929 и окончательно в 1933.

Андрей Николаевич до конца своих дней считал теорию вероятностей главной своей специальностью, хотя областей математики, в которых он работал, можно насчитать добрых два десятка. Но тогда только начиналась дорога Колмогорова и его друзей в науке. Они много работали, но не теряли чувства юмора. В шутку называли уравнения с частными производными «уравнениями с несчастными производными», такой специальный термин, как конечные разности, переиначивался в «разные конечности», а теория вероятностей — в «теорию неприятностей».

Норберт Винер, отец кибернетики, свидетельствовал: «…Хинчин и Колмогоров, два наиболее видных русских специалиста по теории вероятностей, долгое время работали в той же области, что и я. Более двадцати лет мы наступали друг другу на пятки: то они доказывали теорему, которую я вот-вот готовился доказать, то мне удавалось прийти к финишу чуть-чуть раньше их».

В 1930 г. Колмогоров стал профессором МГУ, с 1933 по 1939 год был ректором Института математики и механики МГУ, многие годы руководил кафедрой теории вероятностей и лабораторией статистических методов. В 1935 году Колмогорову была присвоена степень доктора физико-математических наук, в 1939 году он был избран членом АН СССР. Незадолго до начала Великой Отечественной войны Колмогорову и Хинчину за работы по теории вероятностей в 1941 году была присуждена Сталинская премия.

Замечательная закономерность: многие из учеников Колмогорова, обретая самостоятельность, начинали играть ведущую роль в избранном направлении исследований. И академик с гордостью подчеркивает, что наиболее дороги ему ученики, превзошедшие учителя в научных поисках

Можно удивляться колмогоровскому подвижничеству, его способности одновременно заниматься — и небезуспешно! — сразу множеством дел.

Пролистав книгу «А. Н. Колмогоров. Избранные труды. Математика и механика», я была поражёна тем, по скольким темам сосредоточены в ней исследования! Здесь: тригонометрические и ортогональные ряды, теория меры и интеграла, теория приближений, математической логики, интегральные уравнения, геометрия, топология, теория множеств, классическая механика… и вдруг, теория турбулентности.

Турбулентность… и в моей памяти сразу всплывает:

«Уважаемые пассажиры! Наш самолет входит в зону турбулентности. Приведите спинки кресел в вертикальное положение и пристегните ремни». И после этого начинается «болтанка»! Или мелкая и противная, от которой стучат зубы, или и того хуже — самолет то «ухается» в воздушную яму, то подпрыгивает как норовистый скакун. И особенно страшно — у иллюминатора. Слайд 4

Рис. 2. Самолет в зоне турбулентности

 

Потому что видно, как крыло ходит ходуном, того и гляди отвалится!

А тут ещё фильм этот — «Турбулентность»! Только и остается, что сидеть и ждать, когда самолет развалится. Слайд 5

Рис. 3. В салоне самолёта

 

Нет! Больше никогда и никуда не полечу! Только поезд! Вот такими были мои личные ощущения, когда я впервые столкнулась с явлением «Турбулентность», совершая перелёт к месту отпуска со своими родителями.

Что же это за явление такое? — первый вопрос, который я перед собой поставила. Почему столь великий учёный занимался его изучением? — второй вопрос. Для чего это явление следует продолжать изучать? — третий вопрос.

Слайд 6

И, как человек любознательный, провела свою небольшую исследовательскую работу по этим вопросам, о чём и расскажу на сегодняшней конференции.

Основная (содержательная часть).

1. Что же это за явление такое?

Попытаемся ответить на этот вопрос.

Вот как определяют понятие турбулентности различные справочники:

                    В Словаре синонимов турбулентность это беспорядочность

                    В «Большом энциклопедическом» словаре: турбулентное течение (от лат turbulentus — бурный беспорядочный), течение жидкости или газа, при котором частицы жидкости совершают неупорядоченные, хаотические движения.

                    В Физической энциклопедии: явление, наблюдаемое во многих течениях жидкостей и газов и заключающееся в том, что в этих течениях образуются многочисленные вихри различных размеров, вследствие чего их гидродинамические и термодинамические характеристики (скорость, темп-ра, давление, плотность) испытывают хаотические флуктуации и потому изменяются от точки к точке и во времени нерегулярно.

                    В Энциклопедии техники: турбулентность (от лат. turbulentus — бурный, беспорядочный) — физическое явление, характеризующееся нерегулярными взаимными перемещениями объёмов среды (жидкости или газа) и их перемешиванием и сопровождающееся хаотическими изменениями газодинамических переменных в пространстве и времени.

                    В Википедии турбуле́нтность — устаревшее турбуле́нция (от лат. turbulentus — бурный, беспорядочный), по другой версии слово турбулентность происходит от латинского turbo, что переводится как вихрь.

Но больше всего мне понравилось определение в Словаре русского языка Российской академии наук:

Турбулентность — явление, характерное для такого течения жидкости или газа, при котором в потоке образуются многочисленные вихри различных размеров. Красиво, просто и понятно.

Лично для меня эти определения явились настоящим открытием, т. к. я, как и большинство жителей планеты, считала, что это явление происходит только в атмосфере! Я продолжила своё исследование, и оказалось, что турбулентность экспериментально открыта английским инженером Рейнольдсом в 1883 году при изучении течения несжимаемой жидкости, в частности, воды в трубах.

Физическая картина турбулентности образно выражена в следующем четверостишии, написанном английским физиком Л. Ричардсоном в 1922 году:

Big whirls make little whirls

Which feed on their velocity,

Little whirls have smaller ones

And so on into viscosity.

Почти дословный перевод звучит так:

Большие вихри рождают малые завихрения,

Которые питаются их скоростью.

Малые завихрения порождают еще меньшие,

Пока все не погубит вязкость.

В журнале «Успехи математических наук», посвященном юбилею академика А. М. Обухова, коллеги Андрея Николаевича Колмогорова, одного из классиков теории турбулентности, есть стихотворный вариант перевода:

Слайд 7

В поток бурлящий бросив взгляд,

Вихрей увидишь там каскад:

Меньшой у большего энергию берет,

Пока мельчайших вязкость не сотрет.

2. Почему столь великий учёный занимался изучением турбулентности?

В советской науке учёные также занимались этим явлением. В 1938 году Капицей было открыто турбулентное течение в квантовых средах — сверхтекучем гелии. В жидком гелии есть два типа звука — первый и второй, они могут создавать волновую турбулентность на его поверхности. Но значительным прогрессом в изучении фундаментальных проблем турбулентности мы обязаны, прежде всего, А. Н. Колмогорову и А. М. Обухову, их ученикам и последователям. До 1941 года математической теории турбулентности не существовало, но было несколько великих ученых, которые пытались дать феноменологическое объяснение турбулентности. Андрей Николаевич Колмогоров думал о турбулентности примерно полгода. Колмогоровым были опубликованы три маленькие статеечки в «Докладах Академии наук» общим объемом примерно в 15 страниц. Но и этого оказалось достаточно. Из этого выросла математическая теория турбулентности.

В вышедшей в 1998 году монографии французского ученого Уриэла Фриша «Турбулентность. Наследие Колмогорова» содержится более 600 работ последователей Колмогорова. И в этой же монографии есть такие слова: «Глубже всех проник в суть турбулентности именно Колмогоров — математик, обладавший страстным интересом к живой действительности».

Именно со страстным интересом к живой действительности и можно связать изучение этого явления столь великим учёным. Ведь оказывается при определённых параметрах турбулентность наблюдается в потоках жидкостей и газов, многофазных течениях, жидких кристаллах, квантовых Бозе- и Ферми- жидкостях, магнитных жидкостях, плазме и любых сплошных средах (например, в песке, земле, металлах).

Слайд 8

Рис. 4. Кристаллическая турбулентность

 

Турбулентность также наблюдается при взрывах звёзд, в сверхтекучем гелии, в нейтронных звёздах, в лёгких человека и при движении крови в сердце.Выдающийся бельгийский ученый И. Пригожин поставил вопрос о присуждении Колмогорову Нобелевской премии, но слишком поздно, когда Андрею Николаевичу осталось жить всего полгода.

3. Для чего явление турбулентности следует продолжать изучать?

1)     Турбулентный поток крови.

Кровь в норме протекает через все сосуды сердечно-сосудистой системы в виде упорядоченного и линейного потока, который называется ламинарным потоком Слайд 9

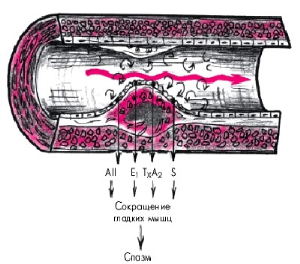
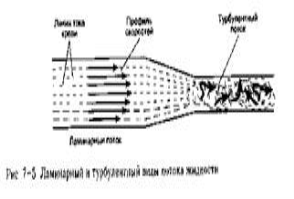
Рис. 5. Турбулентность в крови

 

Скорость наибольшая по центральной оси сосуда и уменьшается почти до нуля у стенки сосуда и концентрические слои жидкости с различной скоростью движения гладко скользят друг относительно друга. Между отдельными слоями жидкости происходит лишь незначительное смешивание, так что отдельные частицы потока перемещаются прямо в отдельных слоях параллельно оси общего потока жидкости. Но кровь является вязкой жидкостью, ее движение через сосуд порождает напряжение сдвига на стенки сосуда. Напряжение сдвига является важным фактором при определенных патологических состояний. Например, атеросклеротические бляшки имеют тенденцию образовываться преимущественно около ответвлений крупных артерий, здесь и наблюдается значительное напряжение сдвига. А когда кровь под давлением с большой скоростью проходит через узкое отверстие, ее нормальный ламинарный поток может превратиться а турбулентный поток. Когда кровоток в сосуде носит турбулентный характер, сопротивление сосуда значительно повышается. При турбулентном движении крови также возникают шумы, которые могут выслушиваться с помощью стетоскопа. Например, сердечные шумы являются проявлениями турбулентного кровотока, возникающего из-за наличия патологии клапанов сердца.

2)     Турбулентность в природе

Все мы видели, что даже легкий ветерок заставляет трепетать флаги, т. е. воздушные потоки имеют вихревую структуру. В природе вихри появляются в той части потока, где скорость быстро меняется в направлении, перпендикулярном потоку. Каждому приходилось видеть вихри в быстрой реке на переходе от быстрины к замедленному течению у берега. Слайд 11

Рис. 6. Естественная турбулентность

 

Физики обнаружили у полярных сияний турбулентные явления.

Слайд 12

Рис. 7. Полярные сияния связаны с турбулентным явлением

 

3)     Турбулентность в атмосфере Земли

Оказалось, что вихревые системы в атмосфере Земли бывают двух видов — циклоны и антициклоны. В Северном полушарии Земли все циклоны вращаются против часовой стрелки, а антициклоны — по часовой, в Южном — наоборот. Направление вихрей определяется силой Кориолиса.

Слайд 13

Рис. 8. Атмосферные вихри, аналогичные смерчам

 

В тропиках циклоны забирают энергию от нагретой поверхности океана и приобретают огромную мощь. За один день большой ураган расходует энергию, равную энергии взрыва 13 000 мегатонных ядерных бомб. Диаметр тропического циклона, его еще называют ураганом или тайфуном, составляет несколько сот километров, высота — до 12–15 км, скорость ветра достигает 400–600 км/час. Самые большие скорости ветра в урагане наблюдаются вокруг так называемого «глаза бури» — зоны покоя в центре урагана.

4)     Турбулентность в океане

Если атмосферные вихри известны давно, аналогичная система океанских течений была обнаружена советскими океанологами в конце 20-го века. Слайд 14

Рис. 9. Океанские течения

 

Это было выдающимся открытием. При изучении этого явления в океане, было замечено, что дельфины могут эффективно подавлять возникновение турбулентности, благодаря чему могут быстро и бесшумно перемещаться в воде. Созданные под влиянием этих исследований специальные покрытия позволили сделать бесшумные подводные лодки. Подводная лодка «Варшавянка», она же «Kilo» или «Черная дыра» обладает шумностью на уровне естественных шумов океана.

Слайд 15

Рис. 10. Подводная лодка «Варшавянка»

 

5)     Турбулентность в космическом пространстве.

В космическом пространстве больших планет также наблюдаются вихревые образования. Особенно удивительно так называемое Красное пятно на Юпитере, вихрь, устойчиво существующий в течение всех лет наблюдений в телескопы. Слайд 16

Рис. 11. Вихрь на Юпитере

 

Рис. 12.Красное пятно на Юпитере

 

В межзвездных туманностях также можно наблюдать вихревые образования. Возможно, что галактики образовались как турбулентные вихри при расширении вещества Вселенной.

Ученые из Университета Айовы решили исследовать эти космические бури. Старший преподаватель физики и астрономии Университета Айовы Грегори Хауэс утверждает: «Бури не являются характерным феноменом лишь для Земли. Они возникают и повсюду в нашей Солнечной Системе, на других планетах и просто в космическом пространстве. Турбулентность может возникнуть и далеко за пределами нашей Солнечной Системы. Космические ветра, которые являются ее виновниками, стимулируют хаотические движения ионизированного газа, плазмы, которые заполняют всю вселенную. Мы думаем, что космическая турбулентность играет ключевую роль в нагревании атмосферы Солнца и солнечной короны до температуры в миллионы градусов Цельсия, что почти в тысячу раз больше, чем поверхность Солнца». Слайд 17

Рис. 13. Космическая турбулентность нагревает атмосферу Солнца

 

Он добавляет: «Космические бури или турбулентность также регулируют формирование звезд повсюду по галактике, распространяет радиацию, испускаемую от массивной черной дыры в центре нашей галактики, и влияет на погоду и климат на нашей планете».

6)     Турбулентность в аэродинамике

Турбулентностью в аэродинамике называют необычное свойство атмосферы, при котором воздух становится неоднородным. Вместе со скоростью ветра увеличивается и турбулентность, поэтому при попадании самолёта в неровные потоки воздуха рекомендуется снижать скорость. В том случае, когда самолёт попадает в зону турбулентности, могут наблюдаться значительные изменения в траектории его полёта, не менее редко самолёт начинает трясти и подбрасывать в воздухе, что может вызывать панику на борту, но и сбить самолёт с нужного курса. Подобное происходит в результате попадания самолёта между нисходящим и исходящим потоками воздуха. Как правило после прохождения зоны турбулентности, самолёт быстро выравнивается и набирает прежнюю скорость и высоту.

Исследование турбулентности привело Н. Е. Жуковского к созданию основ современной теории аэродинамики. Эта теория сделалась основой авиации. Н. Е. Жуковский установил механизм образования подъемной силы крыла в идеальной жидкости, ввел понятие присоединенных, неподвижных относительно крыла, вихрей, стал родоначальником вихревого метода в аэродинамике. Вихревой метод оказался особенно эффективным с появлением компьютеров и созданием численных методов.

Большинство пассажиров испытывают неприятные ощущения во время прохождения самолёта через зону турбулентности. Для многих, однажды пережитая сильная турбулентность послужила толчком к развитию аэрофобии. Однако, важно знать: ТУРБУЛЕНТНОСТЬ НЕ ПРЕДСТАВЛЯЕТ СОБОЙ КАКОЙ ЛИБО УГРОЗЫ ДЛЯ САМОЛЁТА! Турбулентность — это нормальное физическое явление, связанное с неоднородностью воздушных масс и разницы в давлениях на границах разнородных воздушных масс. Говоря простым языком, молекулы воздуха, через которые проходит самолёт неоднородны по своему составу и плотности, следовательно — их несущая способность неодинакова. Так как самолёт проходит через воздух с огромной скоростью, создается вибрация (тряска), ощутимая в салоне самолёта.

Слайд 18

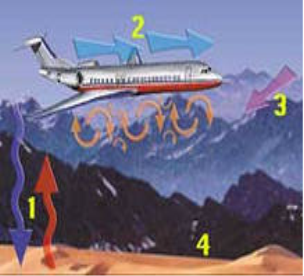
Рис. 14. Самолёт проходит через зону турбулентности

 

Существуют и другие причины турбулентности, в том числе завихрения воздуха от впереди идущего борта и даже от торцов крыльев самого самолёта.

Турбулентность известна почти столько же времени, сколько человек летает на самолётах. Естественно, что при планировке, создании и строительстве самолётов в расчёт берутся данные о тех максимальных нагрузках, с которыми самолёту придётся столкнуться в небе. Среди этих расчётных нагрузок, конечно же, присутствует и турбулентность.

Помните — что турбулентность в полете это ЕСТЕСТВЕННОЕ явление, и необычным оно является только для вас. В день в мире происходит около 130 000 коммерческих рейсов. Из них 87–90 % на том или ином этапе полёта проходят через зону турбулентности. За последние 25 лет не было ни одного случая авиакатастроф, из за попадания самолёта в турбулентную зону. Естественно, что оставаясь пристегнутыми во время полёта вы исключаете риск падения при очень редко возникающих внезапных и сильных турбулентных явлениях.

ВАЖНО ПОНЯТЬ: нагрузка на самолёт при пролёте через самую сильную турбулентность сопоставима с нагрузкой на автомобиль, который едет по не очень ровной дороге. Не более того. Турбулентность в самолете абсолютно безопасна для самолёта. Пассажиры могут получить травмы, если при внезапной турбулентности они будут, например, стоять в проходе и на них из плохо закрытого верхнего багажного отделения упадет, скажем, чемодан. Других опасностей, связанных даже с очень сильной турбулентностью, для пассажиров и самолёта нет.

Заключение

Поскольку турбулентность — одно из глубочайших явлений природы, при самом общем подходе к его изучению оно смыкается с философским проникновением в суть вещей. Знаменитый ученый Т. Карман очень образно охарактеризовал это, сказав, что, когда предстанет перед Создателем, первое откровение, о котором будет просить, — раскрыть тайны турбулентности.

Исчерпывающая математическая модель турбулентности до сих пор не создана. Основы современной теории были заложены великим математиком Андреем Колмогоровым в 40-ые годы XX века. Его работа, в частности, позволила получить уравнения, описывающие разницу скоростей между двумя любыми точками жидкости в турбулентном потоке. В настоящее время ученик Колмогорова А. М. Яглом пишет серию книг по колмогоровской теории турбулентности из семи томов.

Итак, в качестве заключения, предлагаю посмотреть видеоролик.

Интересный факт

Физик Хосе Луис Арагон (Jose Lois Aragon) из мексиканского Национального Автономного Университета (National Autonomous University of Mexico) и его соавторы исследовав математическую модель картины «Звездная ночь», написанную в 1889 году великим голландским художником Винсентом Ван Гогом обнаружили характерные «статистические отпечатки» турбулентности.

Слайд 19

Рис. 15. Винсент Ван Гог «Звездная ночь»

 

Исследователи оцифровали произведения Ван Гога и рассчитали вероятность того, что два пикселя, находящиеся на определенном расстоянии будут обладать одинаковой яркостью. По их мнению, глаз наиболее чувствителен именно к показателям яркости и в ней заложена главная информация картины. Некоторые из работ Ван Гога оказались явно подчинены математическим закономерностям, выявленным Колмогоровым при описании турбулентности, если вместо скоростей точек в потоке рассматривать распределение яркостей.

 

Литература:

 

1. Словарь синонимов./ Ред. А. П. Евгеньева. — М: «Наука», 1976.
2. «Большой энциклопедический» словарь./ Ред. академик А. М. Прохоров. — М.: «Советская энциклопедия», 1979.
3. Физическая энциклопедия. Энциклопедия в пяти томах./ Ред. академик А. М. Прохоров. — М.: «Советская энциклопедия», 1988.
4. Энциклопедия техники: enc-dic.com.
5. Словарь русского языка Российской академии наук в четырёх томах./ Ред. А. П. Евгеньева. — М.: «Русский язык», 1999.
6. Колмогоров А. Н. Избранные труды. Математика и механика. М., 1985.
7. Турбулентность. Наследие А. Н. Колмогорова. У. Фриш. М: ФАЗИС, 1998.
8. http://ru.wikipedia.org/wiki.
9. letaem-bez-straha.ru›Турбулентность.
10. dic.academic.ru›Турбулентность.