Особенности методической подготовки учителей начальной школы в области изучения величин на уроках математики
Авторы: Трофименко Юлия Владимировна, Пинкина Светлана Ивановна
Рубрика: 9. Педагогика высшей профессиональной школы
Опубликовано в
Дата публикации: 26.06.2017
Статья просмотрена: 1893 раза
Библиографическое описание:
Трофименко, Ю. В. Особенности методической подготовки учителей начальной школы в области изучения величин на уроках математики / Ю. В. Трофименко, С. И. Пинкина. — Текст : непосредственный // Аспекты и тенденции педагогической науки : материалы II Междунар. науч. конф. (г. Санкт-Петербург, июль 2017 г.). — Санкт-Петербург : Свое издательство, 2017. — С. 79-83. — URL: https://moluch.ru/conf/ped/archive/216/12695/ (дата обращения: 24.04.2025).
Начальное обучение — первый, а потому особенно ответственный период в системе обучения школьников [10]. Поэтому начальное обучение должно быть построено таким образом, чтобы усвоенные знания явились тем основным фундаментом, на котором будут надстраиваться все последующие знания по учебным предметам общеобразовательной школы. Изучение начального курса математики должно не только вооружить учащихся предусмотренным программой кругом знаний, умений и навыков, но и обеспечить необходимый уровень их общего и математического развития [2].
Сегодня учитель, для того, чтобы полно реализовать дидактические возможности учебников, должен иметь высокий уровень математической подготовки и быть компетентным в дидактических принципах, на которых строятся современные учебники [8].
Современные учебники требуют от учителя профессионального умения формировать у школьников способы познавательной деятельности, интеллектуальных умений. Это позволяет сделать учеников более самостоятельными в решении учебных задач и вооружить умениями более рационально строить свою деятельность по усвоению знаний [9].
Активизация творческой познавательной деятельности учащихся зависит в большей степени от методов обучения, которые использует учитель на уроке. Развитие творческих возможностей учащихся важно на всех этапах школьного обучения, но особое значение имеет формирование творческого мышления в младшем школьном возрасте. Поэтому современная начальная школа предъявляет новые требования к подготовке учителя, она требует учителя, обладающего должным уровнем профессиональной компетентности [11].
В структуре профессиональной компетентности учителя начальных классов на одном из первых мест находится знаниевый компонент. Знания, усвоенные будущим учителем начальной школы в процессе его обучения в вузе, являются средством его профессиональной деятельности. Только твердо зная учебный предмет, учитель сможет понять особенности его представления в учебнике, все достоинства и недостатки учебника и реально проявить свое методическое мастерство [8].
Учителю начальной школы важно, прежде всего, знать теоретические основы каждого раздела начального курса математики; знать какими умениями и навыками должны овладеть учащиеся, изучая тот или иной материал, видеть взаимосвязь между ними и те трудности, которые могут возникнуть у учащихся при изучении конкретного учебного материала. Учителю необходимо знать определенную систему понятий и математических способов доказательств, нужно понять, каковы особенности математических понятий и доказательства. Такие знания нужны учителю начальных классов потому, что он первым вводит детей в мир математических знаний, и от того, как грамотно и успешно он это сделает, зависит и отношение ребенка к изучению математики в дальнейшем [6].
Уроки математики могут и должны быть использованы в целях формирования у детей основ научного мировоззрения. Нужно довести до осознания младшими школьниками связи математики с практикой, показав ее роль и значение для практической деятельности: научить школьников распознавать в явлениях окружающей жизни математические факты (абстракции); применять математику к решению конкретных практических задач; вооружить учеников практическими умениями, необходимыми каждому человеку в повседневной жизни.
Усвоение математики в процессе обучения неизбежно включает в себя усвоение соответствующих понятий. Понятия являются одной из главных составляющих содержания любой научной теории, в том числе и математики. В ходе обучения школьники знакомятся с математическими понятиями, усвоение которых необходимо в целом для познавательного процесса, для реализации цели образования.
Наблюдения за учащимися показывают, что далеко не все из них в должной мере овладевают изучаемыми понятиями. Одним из существенных недостатков в усвоении понятий является их разобщенность.
Большое внимание в начальном курсе математики уделяется понятию «величина». На протяжении всех лет обучения в начальной школе учащиеся изучают несколько величин, их свойства и измерение, операции над величинами, единицы измерения величин.
При формировании представлений о величинах (длине, массе, площади и др.) учитель опирается на опыт младших школьников, уточняет и расширяет его. Так, при ознакомлении с понятием длины сначала используют такие приемы, как сравнение «на глаз», затем прием наложения, на следующем этапе вводятся различные мерки. В ходе практического выполнения таких заданий учащиеся подводятся к самостоятельному выводу о необходимости введения единых общепринятых единицах измерения каждой величины, знакомятся с измерительными инструментами [5].
Следовательно, учителю начальных классов необходимо знать научные основы тех величин, которые изучаются в современном начальном курсе математики.
Понятие величины, как и другие понятия математики, формировалось постепенно в результате абстрагирования от качественных особенностей свойств реальных объектов, в результате чего выделились только количественные отношения. Поэтому величина — это не сама реальность, а лишь отображение свойств окружающей действительности, то есть величина это понятие, введенное для различения критериев сравнения [3].
Ориентирами для определения понятия величины являются следующие характерные особенности этого понятия:
во-первых, величина — это некоторое свойство множества предметов или явлений;
во-вторых, величина — это такое свойство предметов или явлений, которое позволяет их сравнивать и устанавливать пары объектов, обладающих этим свойством в равной мере;
в-третьих, величина — это такое свойство предметов или явлений, которое позволяет их сравнивать и устанавливать, какой из них обладает данным свойством в большей или меньшей мере.
Эти особенности связаны с представлениями человека о величине.
Древнегреческий философ, математик и логик Аристотель, живший во II в. до н. э., писал, что «то или иное количество есть множество, если его можно счесть; есть величина — если его можно измерить». Это высказывание не может служить определением понятия «величина», так как в нем не определено, что значит «счесть», а что значит «измерить». Но в этом высказывании четко проведена грань между двумя видами количеств и между двумя видами чисел — натуральными, используемыми для пересчета элементов конечных множеств, и действительными, применяемыми для выражения результата измерения.
В знаменитых «Началах» Евклида, жившего в III в. до н. э., были четко сформулированы аксиомы, описывающие общие свойства величины (равные одному и тому же равны между собой; если к равным прибавить равные, то и целые будут равны; целое больше своей части и т. д.), называемых теперь для отличия от дальнейших обобщений положительными скалярными величинами [7].
В некоторых математических трудах ученых того времени дается описательное «определение» понятия величины. Например, Герон Александрийский писал, что величина есть все то, что может быть увеличено или разделено безгранично.
Таким образом, уже в тот период математика имела дело с величинами. Но изучала она не отдельные свойства конкретных величин, а общие свойства и отношения объектов математической природы, абстрагированные от конкретного содержания.
В дальнейшем аналогичное понятие величины дает член Петербургской Академии наук Леонард Эйлер (середина XIX в.). Он пишет, что «величина есть то, что способно увеличиваться или уменьшаться». В математическом смысле эти определения не корректны. Они обладают чрезмерной обобщенностью. Им удовлетворяют такие абстрактные понятия, как внимание, правдивость, права или обязанности, которые не поддаются математической трактовке [7].
В современной математике различают скалярные и векторные величины.
Скаляр — величина, каждое значение которой может быть выражено одним (действительным) числом. Другими словами, величина, которая характеризуется только числовым значением без указания какого-либо направления, называется скалярной величиной. Прямая линия, на которой выбраны начало отсчета, единичный отрезок и указано положительное направление, называется числовой осью или шкалой. Слово «шкала» созвучно слову «скала». Видимо, отсюда и происходит термин «скалярная величина», означающая всякую величину, которая характеризуется точками такой шкалы [3].
Примерами скалярных величин являются: температура, отсчитываемая в том или другом направлении от начала отсчета; скорость точки при ее движении по прямой; промежутки времени, отсчитываемые вперед и назад от некоторого начального момента; масса, площадь, объем и др.
Представление о векторных величинах также возникло еще в далеком прошлом. «Вектор» — слово латинского происхождения, означает дословно «несущий, ведущий, переносящий». Понятие «вектор» возникло в связи с изучением величин, характеризуемых числовыми значениями, единицей измерения и направлением [7].
Примерами векторных величин могут служить перемещение, скорость и ускорение поступательно движущегося материального тела, действующая на него сила, напряженность электрического или магнитного поля и др. Чтобы задать, например, векторную величину, нужно указать не только числовое значение величины, но и ее направление. В современной математике раздел, в котором излагается учение о действиях с векторами, называют векторной алгеброй.
В начальном курсе математики рассматривают как векторные, так и скалярные величины, однако приоритетом пользуются скалярные величины.
С конца 19 века, в связи с работами немецкого математика Г. Кантора (1854–1918) в области теории множеств, в специальных учебных пособиях принято следующее определение скалярной величины: скалярными величинами называют такие множества элементов, для которых установлены понятия равенства и неравенства, больше и меньше, а также возможность выражения любого элемента через несколько равных меньших элементов этого множества [7].
Выбор учителем методики обучения величинам младших школьников непосредственно зависит от знания им теоретических основ математики. Глубокие знания теоретических основ изучения величин и математический кругозор предоставляют учителю возможности для поиска методов и технологий обучения величинам младших школьников. Но даже для ориентации в существующих подходах изучения величин и их измерений в содержании различных учебников учителю необходимо знать исходные стержни понятия величины [7].
В современной математике существует несколько подходов к определению понятия скалярной величины: в одном случае она определяется как функция с заданными свойствами, в другом — как множество объектов с некоторой совокупностью свойств, в третьем просто отождествляется с числом. В ряде учебных пособий по математике используется аксиоматический подход к рассмотрению скалярной величины, при котором скалярная величина определяется косвенно через ту или иную систему аксиом. Выбор системы аксиом может быть различным [1]. Поскольку в начальном курсе математики рассматриваются скалярные величины, принимающие только положительное значение (длина, масса, емкость, площадь и др.), то для наших целей достаточно рассмотреть аксиоматику положительных скалярных величин.
В современной математике смысл понятия «величина» достаточно точно определен А. Н. Колмогоровым. В аксиоматике, данной академиком А. Н. Колмогоровым, содержатся и свойства сравнимости элементов множества, и свойства сложения и вычитания, то есть в ней речь идет о положительных скалярных величинах [7].
Согласно А. Н. Колмогорову, первоначальным понятием положительных скалярных величинах является обобщение таких конкретных понятий, как длина, площадь, объем и т. д. Каждый конкретный род величин связан с определенным способом сравнения физических тел или других объектов. (В геометрии, например, отрезки сравниваются путем наложения.)
Положительной скалярной величиной называется всякое множество объектов, в котором установлены отношения равенства и неравенства, а также операция сложения, производимая так, что выполняются следующие аксиомы.
- Каковы бы ни были величины а и b, имеет место одно из трех соотношении: или а = b, или а < b; или b < а (свойство линейности отношений «меньше», «равно»).
- Если а < b и b < с, то а < с (свойство транзитивности отношений «меньше», «больше»).
- Для любых двух величин а и b существует однозначно определенная величина с = а + b.
- Для любых двух величин а и b верно, что а + b = b + а (коммутативное свойство сложения величин).
- а + (b + с) = (а + b) + с (ассоциативное свойство сложения величин).
- а + b > а. Сумма больше каждого из слагаемых (свойство монотонности сложения величин).
- Если а > b, то существует одна и только одна величина с, для которой b + с = а (возможность вычитания величин).
- Каковы бы ни были величина а и натуральное число n, существует такая величина b, что n — b = а (возможность деления величины на число).
- Каковы бы ни были величины а и b, существует такое натуральное число n, что а < n · b. (Это свойство называется аксиомой Архимеда; на нем вместе с более элементарными аксиомами 1–8 основана теория измерения величин, развитая древнегреческими математиками.)
- Если две последовательности величин а1 < а2 < а3 < … и b1 < b2 < b3… обладают тем свойством, что для любой величины с при достаточно большом номере n, bn — an < с, то существует одна единственная величина х, которая больше всех аn и меньше всех bn (аксиома непрерывности).
Система аксиом 1–10 имеет смысл лишь тогда, когда величины а, b и с выражают одно и то же свойство объектов некоторого множества, то есть однородные величины. Например, свойство предмета иметь протяженность называется длиной, поэтому о длинах конкретных объектов говорят, что это величины одного рода. Различные свойства объектов выражаются разнородными величинами. Например, длина и площадь — разнородные величины [7].
Считается, что аксиомы 1–10 вполне определяют современное понятие системы положительных скалярных величин.
В вузовском курсе математики особо отмечается, что не следует смешивать понятие числа с понятием величины. Являясь результатом измерения, число всегда отвлеченно, единично и неспособно ни к какому изменению. Напротив, величина, являясь качеством предмета, всегда конкретна и поэтому всегда в значительной степени склонна к изменению.
При сравнении величин непосредственно устанавливается их равенство или неравенство. Чтобы получить более точный результат, необходимо величины измерить. Измерение — операция, посредством которой определяется отношение одной измеряемой величины к другой однородной величине (принимаемой за единицу). Число, выражающее такое отношение, называется числовым значением измеряемой величины.
Измерить величину — это значит сравнить ее с некоторой величиной того же рода, принятой за единицу, и выразить результат сравнения числом.
Процесс сравнения зависит от рода рассматриваемых величин. Для длин он один, для масс — другой, для измерения промежутков времени — третий и т. д. Каким бы ни был этот процесс, в результате измерения величина выражается определенным числовым значением при выбранной единице измерения.
Отвлеченное число, получающееся как результат измерения данной конкретной величины единицею измерения этого же рода, называется числовым значением рассматриваемой величины.
Следовательно, если дана величина а и выбрана единица измерения величины е, то в результате измерения находят такое действительное число х, что а = хе. Число х называют числовым значением величины а при единице измерения величины е (числовое значение величины есть всегда отвлеченное число).
Согласно этому положению, любую величину можно представить в виде произведения некоторого действительного числа и единицы измерения этой величины. Например, 21,3 кг = 21,3 · 1 кг; 2,7 см = 2, 7 · 1 см; 5 кг = 5 · 1 кг и т. д.
Задача измерения величин позволяет свести сравнение величин к сравнению чисел, а операции над величинами — к соответствующим операциям над числами.
- Если величины а и b измерены при помощи величины е, то отношения между величинами а и b будут такими же, как и отношения между их числовыми значениями, и наоборот:
а = b ![]() me(a) = me(b)
me(a) = me(b)
а < b ![]() me(a) < me(b)
me(a) < me(b)
а > b ![]() me(a) > me(b),
me(a) > me(b),
где тe(а) — числовое значение величины а; me(b) — числовое значение величины b [7].
Например, если объем тела а = 5 см3, объем тела b = 7 см3, то можно утверждать, что при одинаковой плотности масса тела а меньше массы тела b, так как 5 < 7.
-
Если величины а и b измерены при помощи величины е, то, чтобы найти числовое значение суммы а + b, достаточно сложить числовые значения величин а и b: а + b = с
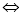 me(а + b) = me(a) + me(b).
me(а + b) = me(a) + me(b).
Например, если а = 3 кг, b = 7 кг, то а + b = 3 кг + 7 кг = (3 + 7) кг = 10кг.
-
Если величины а и b таковы, что b = х · а, х
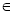 R, и величина а измерена при помощи единицы величины е, то, чтобы найти числовое значение величины b при единице е, достаточно число х умножить на число me(a):
R, и величина а измерена при помощи единицы величины е, то, чтобы найти числовое значение величины b при единице е, достаточно число х умножить на число me(a):
b = х · а ![]() me(b) = х · me(a)
me(b) = х · me(a)
Например, если b = 3а и а = 12 см, то b = 3а = 3 · (12 см) = (3 · 12) см = 36 см.
Литература:
1. Колягин Ю. М. Болевые точки отечественного образования // Начальная школа, 2002. № 4.
2. Концепция содержания непрерывного образования. Дошкольное изначальное звено. Проект // Бюллетень Министерства образования РФ. Высшее и среднее профессиональное образование, 2001. № 1, 3.
3. Меерзон А. Е., Добротворский А. С., Чекин А. Л. Пособие по математике для студентов факультетов начальных классов. М., 1998.
4. Паболкова Н. Н. О понятии величины и признаках ее проявления // Начальная школа, 2004. № 3.
5. Программно-методические материалы. Математика. Начальная школа / Сост. И. А. Петрова, Е. О. Яременко. М., 2001.
6. Стойлова Л. П. Математика: Учебник для студ. высш. пед. учеб. заведений. М., 1999.
7. Тихоненко А. В. Технология изучения понятия величины на уроках математики в начальной школе. Ростов н/Д. Изд-во: «Феникс», 2006.
8. Трофименко Ю. В. Профессиональная компетентность учителя начальных классов в условиях перехода на многоуровневую систему высшего образования // Инновационное развитие образования в регионах Российской Федерации сборник материалов Всероссийской научно-практической конференции / Под редакцией Л. К. Гребенкиной, А. А. Петренко, Т. В. Ганиной, 2013.
9. Трофименко Ю. В. Формирование содержания профессиональной компетентности будущего учителя начальной школы в области изучения естественно-математических дисциплин // Аспирант и соискатель, 2009. № 5.
10. Федеральный закон от 29 декабря 2012 г. № 273-ФЗ «Об образовании в Российской Федерации» // Правовая справочно-информационная система «Гарант».
11. Федеральный компонент государственного стандарта общего образования. Часть I. Начальное общее образование. Основное общее образование / Министерство образования Российской Федерации. М. 2004.











