«Золотое сечение» — божественная пропорция



Актуальность темы обусловлена необходимостью компетентностного подхода при обучении решению текстовых задач, так как задача является основным звеном внутри процесса обучения.

Иоганн Кеплер говорил, что геометрия владеет двумя сокровищами –теоремой Пифагора и «золотым сечением», и если первое из них можно сравнить с мерой золота, то второе — с драгоценным камнем. Теорему Пифагора знает каждый, а вот что такое «золотое сечение» — далеко не все. Так что такое «золотое сечение»? Сегодня вы узнаете об этом.

(Класс делится на три команды, в каждой из них выбирается капитан)

1. Капитаны получают от учителя конверты с заданиями в виде карточек на каждого участника.

Образец карточки.

Лицевая сторона ABC Алгоритм. Измерить отрезки AB, BC и AC. Найти отношенияAB/AC  BC/AB Скажите ваши ответы капитану. Капитан сообщает общий результат учителю (команды получают баллы).

Обратная сторона Алгоритм. Скажи капитану букву (если она есть). Составьте из всех букв слово. Слово укажет «след», где можно найти следующее задание (ответ: ПАРТА).

На сенсорной доске слайд:

«Золотое сечение»— божественная пропорция».

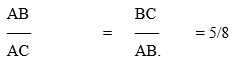
2. Команда по «следу» находит задание (коллективное).

Задание.Разделить отрезок AB в «золотом сечении». (На ватмане дан отрезок AB)

Алгоритм.

1. Измерить отрезок AB, разделить его пополам и поставить точку O (AB: 2 = AO).
2. Из точки B провести перпендикуляр к AB.
3. На перпендикуляре отложить отрезок BD, равный половине AB (например, DB = AO) и соединить точку D и A отрезком.
4. Из точки D провести окружность, радиус которой равен DB. Она пересечет отрезок AD в точке E.
5. Из точки A отложить отрезок AC, равный AE (AC = AE).
6. Измерить CB и AC. Найти отношение CB к AC (CB/AC = 4/6 = 2/3).
7. Показать учителю, что получилось.

(Команды получают 5 баллов за правильное деление отрезка в «золотом сечении»)

3. На сенсорной доске слайд:

Стук в дверь. Вносят 3 конверта, в каждом из которых находятся «следы», где указано, куда идти дальше (конверты отдают капитану).

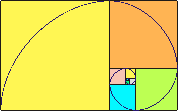
Задание. Найдите в папке в «золотом прямоугольнике» «золотую спираль» и объясните:

1) Почему прямоугольник называется «золотым»? (2 балла)

2) Как строится «золотая спираль»?(4 балла)

3) Вспомните, что в жизни закручено в виде «золотой спирали».

(3 балла)

(Каждая команда выбирает один вопрос из перечисленных выше и отвечает на него)

Ответы.

1.Прямоугольник называется «золотым», так как отношение ширины к длине приближенно равно 0,62.

2. Последовательно строятся квадраты: первый имеет сторону, равную ширине прямоугольника, второй — ширине оставшегося прямоугольника и так далее. Плавной дугой соединяются противоположные вершины квадрата.
3. Улитки, рога, усы в огурцах и вьюнках.

На сенсорной доске слайд

4. Капитаны получают «след» от учителя, на котором указано задание (папки с заданиями и материалом).

Задание для 1-й команды. Изучить материал и представить рассказ о «золотом сечении» в архитектуре и в скульптуре.

Задание для 2-й команды. Изучить материал и представить рассказ о «золотом сечении» в пентаграмме (правильном звездчатом пятиугольнике), в природе.

Задание для 3-й команды. Изучить материал и представить рассказ о «золотом сечении» в искусстве.

Семечки в корзинке подсолнуха выстраиваются вдоль спиралей, которые закручиваются как слева направо, так и справа налево. В одну сторону закручено 13 спиралей, в другую — 21 (13: 21 = 5/8).

В более крупных соцветиях число соответствующих спиралей 21 и 34 (21: 34 = 5/8).

Составление и решение такого рода задач способствует не только лучшему осознанию особенностей структуры и хода решения задач различных видов, но и развитию творческой самостоятельности детей, расширению их кругозора, усилению связи обучения с жизнью.

Изучая дополнительный материал, обучающиеся создают мультимедийные проекты, пишут рефераты.

Проведение имитационной игры.

Игра называется «Следопыт» по теме «Золотое сечение» — божественная пропорция».

Цель:формировать потребность в приобретении новых знаний каждым учеником по теме «Золотое сечение» — божественная пропорция».

Задачи:

1) узнать, что такое «золотое сечение»;

2) узнать, где применяется «золотое сечение».

Класс делится на три команды. В каждой команде выбирается капитан. Игра проходит в виде соревнования. Каждый участник должен найти отношение длин данных отрезков, сравнить отношение отрезков с результатами участников своей команды, сделать вывод. Капитан этот вывод сообщает учителю (ведущему игру). Во втором задании команды с помощью практической работы делят отрезок в «золотом сечении» по алгоритму и подают свой рисунок учителю. В третьем надо догадаться, как получилась «золотая спираль». В четвертом надо обработать имеющуюся информацию о применении «золотого сечения» и донести ее до слушателей. За каждый этап соревнования команды получают баллы. Игра имеет результат, который является финалом игры, придает игре законченность.