От Эвклида до Гёделя: аксиоматический метод в курсе математической логики в вузе
Авторы: Сухан Ирина Владимировна, Кравченко Григорий Григорьевич, Иванисова Ольга Владимировна
Рубрика: 9. Педагогика высшей профессиональной школы
Опубликовано в
III международная научная конференция «Педагогика сегодня: проблемы и решения» (Казань, март 2018)
Дата публикации: 05.03.2018
Статья просмотрена: 186 раз
Библиографическое описание:
Сухан, И. В. От Эвклида до Гёделя: аксиоматический метод в курсе математической логики в вузе / И. В. Сухан, Г. Г. Кравченко, О. В. Иванисова. — Текст : непосредственный // Педагогика сегодня: проблемы и решения : материалы III Междунар. науч. конф. (г. Казань, март 2018 г.). — Казань : Молодой ученый, 2018. — С. 54-59. — URL: https://moluch.ru/conf/ped/archive/276/13936/ (дата обращения: 24.04.2025).
История аксиоматического метода
Понятие аксиоматической теории берет начало от метода, использованного Евклидом при изложении классической геометрии греков. Говоря об истории становления аксиоматического метода, недостаточно привести рассказ о безуспешных попытках доказать пятый постулат Евклидовой геометрии и, в связи с этим, сформулировать отрицание пятого постулата и упомянуть о неевклидовой геометрии. По нашему мнению, стоит подробнее показать причины желания доказать пятый постулат [1].
Первые 28 теорем «Начал» Евклида доказываются без использования пятого постулата и составляют так называемую «абсолютную геометрию». Теорема, обратная теореме № 28, является утверждением, эквивалентным пятому постулату. Видимо, это и было основной причиной стремления доказать её как теорему «абсолютной геометрии». Если бы это удалось, то пятый постулат можно было бы исключить из списка аксиом! Однако все попытки доказать или опровергнуть обратную теорему окончились неудачей [2].
Глубокое исследование пятого постулата, основанное на совершенно оригинальном принципе, провёл в 1733 году итальянский математик Джироламо Саккери. Идея Саккери состояла в том, чтобы заменить пятый постулат противоположным утверждением, вывести из новой системы аксиом как можно больше следствий, тем самым построив «ложную геометрию», и найти в этой геометрии противоречия. Тогда справедливость пятого постулата будет доказана от противного. Допустив ошибку в рассуждениях, Саккери пришел к противоречию, и считая, что доказал пятый постулат, закончил исследование.
Неевклидова геометрия
В первой половине XIX века по пути, проложенному Саккери, пошли К. Ф. Гаусс, Я. Бойяи, Н. И. Лобачевский и Ф. К. Швайкарт. Но цель у них была уже иная — не разоблачить неевклидову геометрию как невозможную, а наоборот, построить альтернативную геометрию и выяснить её возможную роль в реальном мире.
Лобачевский и Бойяи почти одновременно, независимо друг от друга опубликовали изложение того, что сейчас называется геометрией Лобачевского. Истинность этой новой геометрии вначале казалась сомнительной. Однако геометрия Лобачевского, как и геометрия Евклида, рассматриваемая как дедуктивная система, оказалась непротиворечивой — в ней не было обнаружено противоречивых утверждений.
Далее были построены различные модели геометрии Лобачевского средствами геометрии Евклида. Из этих интерпретаций следует относительная непротиворечивость геометрии Лобачевского, то есть если геометрия Евклида представляет собой непротиворечивую систему, то геометрия Лобачевского также является непротиворечивой системой.
Аксиоматические теории
Появление парадоксов в теории множеств привлекло к вопросам оснований математики внимание практически всех ведущих математиков начала ХХ века. Была проделана большая работа по теоретико-множественному обоснованию математических и логических понятий. Основным итогом этой деятельности является становление математической логики как самостоятельной математической дисциплины, а принципиальным достижением математической логики — разработка современного аксиоматического метода.
Открытие неевклидовой геометрии, а также построение различных моделей геометрии Лобачевского средствами геометрии Евклида означало отказ от обязательного приписывания какого-либо физического смысла таким исходным понятиям, как точка, прямая, плоскость и позволяло приписывать различные значения первичным терминам аксиоматической теории. Отношение к аксиомам также претерпело решительные изменения.
Эволюция взглядов на природу аксиоматического метода привела к следующей концепции аксиоматической теории [3].
Выбирается несколько первоначальных понятий, которые не определяются и используются без объяснения их смысла. Все другие понятия, которые будут использоваться, должны быть определены через первоначальные понятия и через понятия, смысл которых был определен ранее.
Затем выбирается несколько утверждений (высказываний, формул) о первоначальных и определяемых понятиях, эти утверждения объявляются истинными и называются аксиомами теории.
После этого, пользуясь правилами логического умозаключения, выводят новые утверждения о первоначальных и определяемых понятиях, которые называются теоремами.
Доказательством называется конечная последовательность высказываний (формул) теории w1, w2, …, wk, каждое из которых либо является аксиомой, либо выводится из одного или нескольких предыдущих высказываний (формул) этой последовательности по правилам вывода.
Теоремой называется высказывание (формула), являющееся последним в доказательстве.
Аксиоматической теорией называют систему из двух множеств высказываний (формул) T и W, таких, что ![]() . МножествоWсостоит из всех высказываний (формул) данной теории, множество T состоит из доказуемых высказываний (формул) данной теории, называемых теоремами, выводимых из заданного множества высказываний (формул)
. МножествоWсостоит из всех высказываний (формул) данной теории, множество T состоит из доказуемых высказываний (формул) данной теории, называемых теоремами, выводимых из заданного множества высказываний (формул) ![]() , называемых аксиомами.
, называемых аксиомами.
Основными свойствами аксиоматических теорий являются непротиворечивость иполнота. Непротиворечивость теории означает невозможность вывода в данной теории некоторой формулы и ее отрицания. Полнота теории означает возможность вывода для любой формулы либо самой этой формулы, либо ее отрицания.
В математической логике рассматривают неформальные и формальные аксиоматические теории.
Неформальные аксиоматические теории служат для построения содержательных математических теорий (геометрия, арифметика, теория вероятностей, теоретическая механика и т. п.). Правила вывода в неформальную аксиоматическую теорию не включаются — используется какая-либо известная система логических правил вывода.
Формальные аксиоматические теории рассматривают, если предметом изучения является некоторая математическая теория. Правила вывода включаются в формальную аксиоматическую теорию.
Неформальные аксиоматические теории
При построении неформальной аксиоматической теории обычно исходят из некоторой достаточно развитой интуитивной теории и предполагают известной систему формальной классической логики.
Первым шагом в построении неформальной аксиоматической теории является составление перечня объектов данной теории S0ивыбор символов для их обозначения. Эти символы называются первичными терминами или первичными символами.
Вторым шагом в построении неформальной аксиоматической теории является составление перечня основных свойств T0 отобранных объектов, то есть высказываний об основных объектах, и запись их при помощи первичных символов. Эти свойства называются аксиомами.
Упорядоченная пара множеств
Далее выводят из аксиом теоремы, то есть строят множество T.
Интерпретацией неформальной аксиоматической теории называется приписывание значений (смысла) первичным терминам теории.
Моделью неформальной аксиоматической теории называется совокупность объектов, выбранных в качестве ее интерпретации, удовлетворяющих аксиомам теории.
Неформальная аксиоматическая теория называется непротиворечивой, если она не содержит такого высказывания A, что A и ![]() являются теоремами.
являются теоремами.
Проблему полноты для неформальных аксиоматических теорий не рассматривают, так как ответ на вопрос о том, является некоторая формула неформальной аксиоматической теории теоремой или нет, может зависеть от выбора системы логических правил вывода.
Формальные аксиоматические теории
При изложении содержательных математических теорий широко используются символы, которые заменяют некоторые математические объекты (точки, прямые, числа, вектора, матрицы, функции и т. п.). В отличие от обычного употребления символов в математике, в формальных аксиоматических теориях символы не заменяют собой никаких других объектов. Символы в формальных аксиоматических теориях трактуются как значки, с которыми обращаются согласно определенным правилам, зависящим лишь от формы выражений, образованных из символов.
Для построения формальной аксиоматической теории используется формальный язык теории.
Алфавитом A(T)формальной аксиоматической теории называется непустое конечное множество символов, называемых буквами. Словом или выражением валфавитеA(T)называется любая конечная последовательность букв.
Формальным языком формальной аксиоматической теории называется пара
Формулами вформальной аксиоматической теории являются последовательности символов определенного вида, то есть не всякое слово (выражение) является формулой данной формальной аксиоматической теории.
Из множества формул выделяется некоторое подмножество формул, называемых аксиомами.
Задается конечное множество отношений между формулами, называемых правилами вывода.
Выводом в формальной аксиоматической теории называется конечная последовательность формул этой теории B1, B2, …, Bn, каждая из которых либо является аксиомой, либо выводится из одной или нескольких предыдущих формул этой последовательности по одному из правил вывода.
Формула Ф формальной аксиоматической теории называется теоремой, если существует вывод, последней формулой которого является Ф.
Формальные аксиоматические теории в математической логике принято называть исчислениями.
Простым примером формальной аксиоматической теории является исчисление высказываний.
Доказано, что исчисление высказываний является полной и непротиворечивой формальной аксиоматической теорией.
Для формализации рассуждений, которые не могут быть обоснованы в рамках исчисления высказываний, в математической логике используют исчисление предикатов.
Интерпретацией языка формальной аксиоматической теории называется соответствие, сопоставляющее каждому элементу языка теории единственный элемент некоторого множества D,называемого областью интерпретации.
Моделью формальной аксиоматической теории называетсяинтерпретация языка формальной аксиоматической теории, в которой истинны все аксиомы теории.
Например, моделью исчисления высказываний является алгебра высказываний.
Для формализации математических теорий в математической логике используют формальные аксиоматические теории первого порядка, в которых не допускаются предикаты, имеющие аргументами предикаты и функции, а также не допускаются кванторы по предикатам и функциям.
Язык формальной аксиоматической теории первого порядка совпадает с языком исчисления предикатов. Термы и формулы теории первого порядка определяются также как и в исчислении предикатов.
Аксиомы теории первого порядка разбивают на два класса: логические аксиомы исобственные (нелогические) аксиомы.
Перечни логических аксиом и правил вывода теорий первого порядка
это — дополненные соответствующие перечни исчисления высказываний.
Собственные аксиомы не могут быть сформулированы в общем случае и меняются от теории к теории.
Доказано, что исчисление предикатов первого порядка является полной и непротиворечивой теорией.
Моделью исчисления предикатов первого порядка является логика предикатов.
Формальная арифметика
Первое, полуаксиоматическое, построение арифметики было предложено в
1901 году Дедекиндом и стало известно под названием «система аксиом Пеано».
Аксиомы этой системы формулируются следующим образом:
- 0 есть натуральное число.
- Для любого натурального числа x существует другое натуральное число, обозначаемое x и называемое следующее за x.
- 0 x для любого натурального числа x.
- Если x = y, то x = y.
- Если Q есть свойство, которым обладает натуральное число 0, и для всякого натурального числа x из того, что x обладает свойством Q, следует, что и натуральное число x обладает свойством Q, то свойством Q обладают все натуральные числа.
Пятую аксиому принято называть принципом индукции.
Этих аксиом достаточно для построения не только арифметики натуральных чисел, но и для построения теорий рациональных, вещественных и комплексных чисел.
Однако эта система аксиом содержит такое интуитивное понятие, как «свойство», что не позволяет ей быть формальной аксиоматической теорией.
Для формализации теорий, подобных арифметике, в математической логике используют формальные аксиоматические теории первого порядка сравенством [3].
Для вывода всех основных результатов элементарной арифметики была построена теория первого порядка S.
Теория S имеет следующие собственные аксиомы:
-
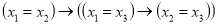 .
.
-
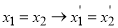 .
.
-
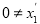 .
.
-
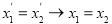 .
.
-
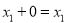 .
.
-
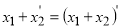 .
.
-
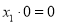 .
.
-
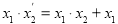 .
.
-
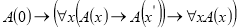 , где
, где 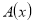 — произвольная формула теории S.
— произвольная формула теории S.
Девятую аксиому принято называть принципом математической индукции.
С помощью правила отделения из девятой аксиомы получается следующее правило индукции: из![]() и
и ![]() выводится
выводится![]() .
.
Рассмотрим интерпретацию теории S, в которой:
- Множество всех неотрицательных чисел служит областью интерпретации.
- Целое число 0 интерпретирует символ «0».
- Прибавление единицы интерпретирует операцию взятия следующего.
- Обычные сложение и умножение интерпретируют операции «+» и «∙».
- Символ «=» интерпретируется как отношение тождества.
Если считать истинность аксиом теории S в этой интерпретации интуитивно очевидной, то эта интерпретация является моделью теории S. Эта модель называется стандартной моделью теории S.
Термы 0;0;0;0;…в теории S называют цифрами и обозначают соответственно 0; ![]() ;
; ![]() ;
; ![]() ;…, то есть 0 с nштрихами обозначают
;…, то есть 0 с nштрихами обозначают ![]() .
.
В теории S можно ввести отношение порядка и понятие делимости. Далее можно показать, что теоремы, доказываемые в курсах элементарной теории чисел можно перевести на язык теории S и построить вывод полученной теоремы.
Для сокращения утверждения: «A есть теорема теории S» применяют запись ![]() .
.
Арифметические функции иарифметические отношения
Для изучения основных свойств теории S — непротиворечивостииполноты — используют арифметические функции и арифметические отношения, которые являются понятиями стандартной модели теории S.
Арифметическими функциями называются функции, у которых область определения и множество значений состоит из натуральных чисел.
Арифметическими отношениями называются отношения, заданные на множестве натуральных чисел.
Арифметическое отношение R(x1,…, xn) называется выразимым в теории S, если существует формула A(x1,…, xn) теории S с n свободными переменными такая, что для любых натуральных чисел k1,…, kn выполняются условия: если R(k1,…, kn)истинно, то ![]() и если R(k1,…, kn)ложно, то
и если R(k1,…, kn)ложно, то![]() .
.
В теориях первого порядка с равенством выражения вида «существует один и только один x такой, что A(x)» символически можно записать так: ![]() , для сокращения используют запись
, для сокращения используют запись ![]() .
.
Арифметическая функция f(x1,…, xn) называется представимой в теории S, если существует формула A(x1,…, xn+1) теории S со свободными переменными x1,…, xn+1 такая, что для любых натуральных чисел k1,…, kn+1 выполняются условия:
1. Если f(k1,…, kn) = kn+1, то ![]() .
.
2. ![]() .
.
Характеристической функцией отношения R(x1,…, xn) называется функция
CR(x1,…, xn), которая равна 1, если отношение R(x1,…, xn) истинно, и равна 0, если отношение R(x1,…, xn) ложно.
При изучении представимости арифметических функций в теории S в качестве простейших функций выбраны следующие функции:
- Нуль-функция: Z(x) = 0 при всех x.
- Прибавление единицы: N(x) = x + 1 при всех x.
-
Проектирующие функции:
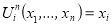 при всех x1,…, xn, i = 1,…, n.
при всех x1,…, xn, i = 1,…, n.
Для получения новых функций из простейших используют операции: суперпозиция функций, схема примитивной рекурсии и операция минимизации
(-оператор).
Функция f(x1,…, xn)называется примитивно рекурсивной, если она может быть получена из исходных функций с помощью конечного числа суперпозиций функций и схем примитивной рекурсии.
Функция f(x1,…, xn)называется частично рекурсивной, если она может быть получена из исходных функций с помощью конечного числа суперпозиций функций, схем примитивной рекурсии и операций минимизации.
Функция f(x1,…, xn)называется общерекурсивной или рекурсивной, если она частично рекурсивна и всюду определена.
Доказано, что класс рекурсивных функций совпадает с классом функций представимых в теории S.
Отношение R(x1,…, xn)называется примитивно рекурсивным, если примитивно рекурсивной является его характеристическая функция CR(x1,…, xn).
Отношение R(x1,…, xn)называется рекурсивным, если рекурсивной является его характеристическая функция CR(x1,…, xn).
Теорема. Всякаярекурсивная функция представима в теории S.
Теорема. Всякоерекурсивное отношение выразимо в теории S.
Гёделева нумерация формул ивыводов вформальной арифметике
В 1931 году Гёделем была предложена нумерация символов, выражений и конечных последовательностей теорий первого порядка с целью арифметизации метаматематики, то есть с целью замены утверждений о формальной системе эквивалентными высказываниями о натуральных числах.
Каждому символу u произвольной теории первого порядка ставится в соответствие положительное число g(u), называемое гёделевым номером символа u, следующим образом:
g(() = 3; g()) = 5; g(,) = 7; g() = 9; g() = 11;
g(xk) = 5 + 8k, где k = 1, 2, …;
g(ak) = 7 + 8k, где k = 1, 2, …;
![]() для k, n 1;
для k, n 1;
![]() для k, n 1.
для k, n 1.
Гёделев номер выражения u0u1…ur определяется следующим образом: ![]() , где pi есть i-епростое число, при этом p0 = 2.
, где pi есть i-епростое число, при этом p0 = 2.
Гёделев номер последовательности выражений e0, e1,…, er определяется следующим образом: ![]() , где pi есть i-епростое число, при этом p0 = 2.
, где pi есть i-епростое число, при этом p0 = 2.
Таким образом, функция g взаимно однозначно отображает множество всех символов, выражений и конечных последовательностей выражений в множество целых положительных чисел.
Теорема Гёделя онеполноте формальной арифметики
Теория первого порядка называется -непротиворечивой, если для всякой формулы A(x)этой теории из того, что при любом n
Доказано, что -непротиворечивая теория первого порядка является непротиворечивой.
Если признать стандартную интерпретацию теории S в качестве модели этой теории, то тогда теорию S следует признать -непротиворечивой.
Для доказательства неполноты формальной арифметики используется примитивно рекурсивное отношение W1(u, y)=«u есть гёделев номер формулы A(x1), содержащей свободную переменную x1, и y есть гёделев номер вывода в S формулы ![]() » [5].
» [5].
Так как отношение W1(u, y) примитивно рекурсивно, то оно выразимо в теории S некоторой формулой V1(x1, x2) с двумя свободными переменными x1, x2.
Рассмотрим формулу ![]() . Пусть m — гёделев номер этой формулы. Подставим в эту формулу
. Пусть m — гёделев номер этой формулы. Подставим в эту формулу ![]() вместо x1, получим замкнутую формулу:
вместо x1, получим замкнутую формулу: ![]() .
.
Теорема (Гёдель, 1931 год). Если теория S непротиворечива, то формула ![]() невыводима в теории S,иесли теория S -непротиворечива, то формула
невыводима в теории S,иесли теория S -непротиворечива, то формула ![]() невыводима в теории S. Доказательство смотри в [4].
невыводима в теории S. Доказательство смотри в [4].
Таким образом, в непротиворечивой теории S невыводимы как формула ![]() , так и ее отрицание
, так и ее отрицание ![]() .
.
Рассмотрим стандартную интерпретацию неразрешимого предложения ![]() .
.
Так как V1 выражает в теории S отношение W1, то, в соответствии со стандартной интерпретацией, формула ![]() утверждает, что отношение W1(m, x2) ложно для любого натурального числа x2, а это означает, что не существует вывода формулы
утверждает, что отношение W1(m, x2) ложно для любого натурального числа x2, а это означает, что не существует вывода формулы ![]() в теории S. Таким образом, формула
в теории S. Таким образом, формула ![]() утверждает свою собственную невыводимость в теории S.
утверждает свою собственную невыводимость в теории S.
Из теоремы Гёделя следует, что если теория S непротиворечива, то эта формула и в самом деле невыводима в теории S и поэтому истинна при стандартной интерпретации.
Итак, в стандартной интерпретации формула
В теореме Гёделя содержится предположение о -непротиворечивости теорииS. Однако ценой некоторого усложнения доказательства можно ограничиться предположением об обычной непротиворечивости теории S. В этом случае необходимо будет воспользоваться примитивно рекурсивным отношением W2(u, y) = «u есть гёделев номер формулы A(x1), содержащей свободную переменную x1, и y есть гёделев номер вывода в S формулы ![]() ».
».
Так как отношение W2(u, y) примитивно рекурсивно, то оно выразимо в теории S некоторой формулой V2(x1, x2) с двумя свободными переменными x1, x2. Значит, если W2(k1, k2)истинно, то ![]() , и если W2(k1, k2) ложно, то
, и если W2(k1, k2) ложно, то ![]() .
.
Рассмотрим формулу ![]() . Пусть n — гёделев номер этой формулы. Подставим в эту формулу
. Пусть n — гёделев номер этой формулы. Подставим в эту формулу ![]() вместо x1 — получим замкнутую формулу:
вместо x1 — получим замкнутую формулу: ![]() .
.
Теорема (Россер, 1936 год). Если теория S непротиворечива, то в ней невыводимы обе формулы ![]() и
и ![]() и, следовательно, существует неразрешимое предложение этой теории.
и, следовательно, существует неразрешимое предложение этой теории.
Эту теорему называют теоремой Гёделя в форме Россера.
Теорема Гёделя онепротиворечивости формальной арифметики
Для доказательства непротиворечивости формальной арифметики помимо отношений W1(u, y) и W2(u, y)используется примитивно рекурсивное отношение
Pf(y, x) = «y есть гёделев номер вывода в S формулы с гёделевым номером x»,выразимое в теории S с помощью некоторой формулы Pf(x1, x2).
Далее, если x — гёделев номер формулы A, то через Neg(x) обозначают гёделев номер формулы ![]() . Доказано, что функция Neg(x)рекурсивна и, следовательно, представима в теории S некоторой формулой Neg(x1, x2) [5].
. Доказано, что функция Neg(x)рекурсивна и, следовательно, представима в теории S некоторой формулой Neg(x1, x2) [5].
Формула ![]() в стандартной интерпретации выражает невозможность вывода в теории S какой-либо формулы вместе с ее отрицанием и является истинной в том и только том случае, когда теория S непротиворечива. Иными словами, эту формулу можно интерпретировать как утверждение непротиворечивости теории S.
в стандартной интерпретации выражает невозможность вывода в теории S какой-либо формулы вместе с ее отрицанием и является истинной в том и только том случае, когда теория S непротиворечива. Иными словами, эту формулу можно интерпретировать как утверждение непротиворечивости теории S.
Вторая теорема Гёделя. Если теория S непротиворечива, то в ней невыводима формула, утверждающая непротиворечивость теории S.
Другими словами, если теория S непротиворечива, то доказательство непротиворечивости теории S не может быть проведеносредствами самой теории S.
Литература:
- Смилга В. П. В погоне за красотой. — М.: «Молодая гвардия», 1968. — 288 с.
- Сухан И. В., Кравченко Г. Г., Иванисова О. В. К вопросу о методике изучения аксиоматического метода в курсе математической логики в вузе. // Педагогика высшей школы. — 2016. — № 3. — С. 125–128.
- Сухан И. В., Кравченко Г. Г., Иванисова О. В. Аксиоматические теории в курсе математической логики // Педагогика высшей школы. — 2017. — № 3. — С. 28–38.
- Сухан И. В., Кравченко Г. Г., Иванисова О. В. Построение формальной арифметики в рамках изучения аксиоматических теорий в вузе. // Педагогика высшей школы. — 2018. — № 1. — С. 00–00.
- Мендельсон Э. Введение в математическую логику. — М.: Наука, 1976. — 320 с.
Похожие статьи
Диофантовы уравнения: от древности до наших дней
Статья посвящена одному из разделов теории чисел — диофантовым уравнениям — как средству реализации интеграционных связей математического образования.
Похожие статьи
Диофантовы уравнения: от древности до наших дней
Статья посвящена одному из разделов теории чисел — диофантовым уравнениям — как средству реализации интеграционных связей математического образования.











