Ликвидация пробелов в знаниях при изучении темы «Решение уравнений»
Автор: Добрынина Ольга Михайловна
Рубрика: 5. Педагогика общеобразовательной школы
Опубликовано в
Дата публикации: 20.06.2018
Статья просмотрена: 710 раз
Библиографическое описание:
Добрынина, О. М. Ликвидация пробелов в знаниях при изучении темы «Решение уравнений» / О. М. Добрынина. — Текст : непосредственный // Аспекты и тенденции педагогической науки : материалы IV Междунар. науч. конф. (г. Санкт-Петербург, июль 2018 г.). — Санкт-Петербург : Свое издательство, 2018. — С. 32-35. — URL: https://moluch.ru/conf/ped/archive/280/14395/ (дата обращения: 10.04.2025).
Математика — наиболее точная из наук. Учебный предмет «Математика» обладает исключительным воспитательным потенциалом: воспитывает интеллектуальную корректность, критичность мышления, способность различать обоснованные и необоснованные суждения, приучает к продолжительной умственной деятельности. Главная цель — создать условия для формирования УУД и развития умений их применять при решении познавательных и учебно — практических задач. В связи с этим одной из важнейших задач становится формирование у школьников представлений о сущности математики как науки. Поэтому на своих уроках я преподаю учащимся математику как живую науку. Соглашусь с Н. И. Лобачевским, что математика — это язык, на котором говорят все точные науки.
На уроке математики во 2 классе ОНЗ (открытия нового знания) по программе «Перспектива» учащиеся знакомятся с новыми видами уравнений: а * х = b; а: х = b; х: а = b. Учащимся на уроке следует выполнить следующие виды математических действий:
– соотнести компоненты умножения и деления со сторонами и площадью прямоугольника;
– построить общий способ решения уравнений вида a x = b; a: x = b; x: a = b на основе взаимосвязи между сторонами и площадью прямоугольника, записать его с помощью алгоритма, решать уравнения данного вида, используя построенный алгоритм, комментировать решение и выполнить проверку решения;
– решить задачи на нахождение сторон, периметра и площади фигур, составленных из прямоугольников;
– составить исравнить числовые и буквенные выражения, определить порядок действий в выражениях, найти их значения наиболее рациональным способом, построить иисполнить вычислительные алгоритмы, закрепить изученные приемы устных и письменных вычислений;
– решить простые и составныезадачи (2−3 действия), сравнить различные способы решения, найти наиболее рациональный способ;
– использовать таблицы для представления результатов выполнения задания;
– составить задачи по самостоятельно составленному выражению, а также задачи с различными величинами, имеющие одинаковое решение;
– начертить на клетчатой бумаге фигуры, равные данной, определить виды углов и виды многоугольников (в зависимости от числа сторон и вершин);
– выполнить заданияпоискового и творческого характера.
Учитель, совместно с учащимися выводит эталоны по открытию новых знаний реализации построенного проекта.
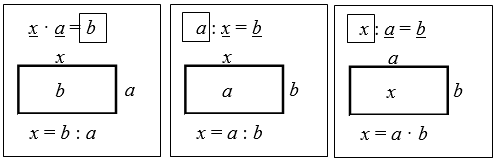
Рис. 1.
При этом очень важно, чтобы учащиеся выучили алгоритм решения уравнений.
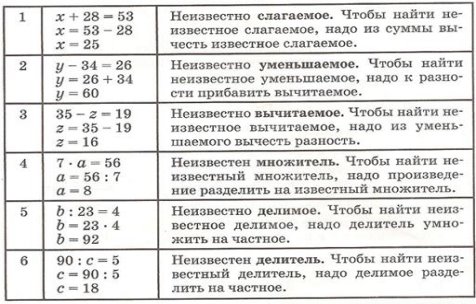
Рис. 2.
На дом учащимся, по желанию, было предложено составить и решить свои уравнения. Из самых лучших уравнений я создала сборник. Заинтересовывая ребят, овладевая способами решения уравнений, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.). Кто придумал уравнения? Ответить на этот вопрос невозможно! Задачи, приводящие к решению простейших уравнений, люди решали на основе здравого смысла. Еще 3–4 тысячи лет до нашей эры египтяне и вавилоняне умели решать простейшие уравнения, вид которых не был похож на современные. Греки унаследовали знания египтян, и пошли дальше. Наибольших успехов в развитии учения об уравнениях достиг греческий ученый Диофант «Он уйму всяких разрешил проблем. И засухи предсказывал и ливни. Поистине его познанья дивны». Большой вклад внес среднеазиатский ученый Мухаммед аль Хорезми (IX век) — среднеазиатский математик, астроном, историк, географ — один из крупнейших ученых средневековья. Его труды по арифметике, изложенные в «Книге об индийском счете», привели к грандиозным последствиям в науке вообще и древней математики.
В математике, как ни в одной другой науке, особенно сильна взаимосвязь материала. Поэтому большое значение имеют прочные систематические знания. Но всегда есть учащиеся, которые не усвоили изученный материал. Основные причины существующих пробелов в знаниях учащихся, на мой взгляд, следующие:
1) незнание познавательных особенностей учащихся;
2) невнимательность на уроках, непонимание до конца излагаемого материала;
3) большое количество пропусков по болезни.
Для ликвидации обнаруженных пробелов применяю следующие приемы.
Самый удобной способ проверки знаний таких учащихся — это карточки, тесты, тренажеры, хороший результат дают работа в парах, группах. Помогают в работе с такими учащимися карточки взаимного контроля, который может быть проведен и по теоретическим вопросам, и по практической части.
Некоторые учащиеся не могут отличить уравнение и буквенные выражения, поэтому таким детям предлагаются следующие задания.
- Уравнение — это:
а)равенство, содержащее букву, значение которой надо найти;
б)числовое равенство;
в)буквенное выражение.
- Корнем уравнения называется: а) любое значение буквы;
б) значение буквы, при котором из уравнения получается верное числовое равенство; в) значение буквы, при котором из уравнения получается неверное числовое равенство.
Впишите пропущенные слова
–Равенство, имеющее переменную, называется______________________
–Решить уравнение — это найти__________________уравнения
–Значение переменной, обращающее уравнение в верное равенство, называется__________________________уравнения
–Правильно ли решено уравнение поможет выяснить____________________
–Подчеркните среди предложенных выражений уравнение:
130 + 34–100 = 64 34 < 32 + 70 25 * а =100
Некоторые дети очень формально подходят к проверке найденных корней. Проводят черту, вместо неизвестного ставят найденное значение и на этом проверку считают законченной, проводить вычисления уже не считают нужным, поэтому таким ученикам нужно предлагать задания, где без проверки нельзя получить верный ответ. Ученики должны понять, что проверка нужна им, а не учителю, именно проверка дает гарантию правильного решения.
Укажите номера верных утверждений:
1)Корнем уравнения называют значение буквы.
2)Уравнение — это равенство, содержащее букву, значение которой надо найти.
3)Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
4)Уравнение х — х = 0 имеет ровно один корень.
5)Любое натуральное число является корнем уравнения
ИНДИВИДУАЛЬНЫЕ КАРТОЧКИ (ДЛЯ РАБОТЫ В ПАРЕ)
Решите уравнения:
1) 47 + x =95
2) 3 * х = 81
3) 25 — у =16
4) а: 45 =5
Задание: Соедините линиями соответствующие части определений
|
Чтобы найти неизвестное слагаемое, надо |
Из суммы вычесть известное слагаемое |
|
Чтобы найти неизвестное уменьшаемое, надо |
из уменьшаемого вычесть разность. |
|
Чтобы найти неизвестное вычитаемое, надо |
к разности прибавить вычитаемое. |
|
Чтобы найти неизвестный множитель, надо |
частное умножить на делитель. |
|
Чтобы найти неизвестное делимое, надо |
произведение разделить на другой множитель. |
|
Чтобы найти неизвестный делитель, надо |
делимое разделить на частное. |
Нужно вспомнить, что при сложении и умножении отличных от 0 чисел, в результате получаем большее число, а вот при вычитании и делении результат будет меньше.
На каждом уроке была организована продуктивная деятельность. Планомерное и систематическое повторение — верный путь к ликвидации пробелов в знаниях учащихся. Но, как и при объяснении нового материала, так и при повторении не все учащиеся хорошо усваивают знания. Поэтому работа по выявлению и последующей ликвидации пробелов в знаниях каждого учащегося должна вестись в течение всего периода обучения. Низкий уровень заметно понизился. Увеличилось количество учеников, которые показали высокие уровни УУД.
Важно помнить, чтобы урок был интересен для каждого ученика. Необходим контроль выполнения домашних работ, консультации, дополнительные занятия и работа со слабоуспевающими учащимися. Тогда не пропадает интерес к предмету, а отсюда и пробелов в знаниях будет меньше, а значит и времени на их устранение понадобится меньше. Чтобы предмет математики был интересен для учеников, чтобы каждый чувствовал себя успешным, необходим ежедневный напряженный и кропотливый труд учителя. Каждый урок должен быть поиском.
Литература:
1. Кочергина А. В. Учим математику с увлечением. М.: 5 за знания,2008. С.159
2. Сухарева Л. С. Как помочь младшему школьнику по математике. М.: Ранок,2010. С. 157.











