Модульное обучение в рамках реализации межпредметных связей в условиях ФГОС
Авторы: Новикова Ольга Вячеславовна, Мореншильдт Ирина Кирилловна, Черепова Ксения Григорьевна
Рубрика: 1. Общая педагогика
Опубликовано в
Дата публикации: 28.09.2019
Статья просмотрена: 121 раз
Библиографическое описание:
Новикова, О. В. Модульное обучение в рамках реализации межпредметных связей в условиях ФГОС / О. В. Новикова, И. К. Мореншильдт, К. Г. Черепова. — Текст : непосредственный // Теория и практика образования в современном мире : материалы XI Междунар. науч. конф. (г. Санкт-Петербург, октябрь 2019 г.). — Санкт-Петербург : Свое издательство, 2019. — С. 2-5. — URL: https://moluch.ru/conf/ped/archive/343/15327/ (дата обращения: 24.04.2025).
Новые федеральные государственные образовательные стандарты направлены на усиление содержательной части школьной программы и должны способствовать развитию здорового образа жизни учащихся.
С данной точки зрения, стратегия социального проектирования ФГОС определяет способы достижения личностного и познавательного развития обучающихся.
Согласно данным нового стандарта основного общего и среднего (полного) образования обучающийся должен быть развитой личностью, обладающей целостным мировоззрением, способностью к самореализации в будущей профессиональной и общественной деятельности в качестве полноценного члена общества [1].
Ориентация на достижение личностного и метапредметного результата обучения становится приоритетной в учебной деятельности, что способствует формированию целостной картины мира. Очень часто при изучении предметов школьной программы обучающимся сложно самостоятельно найти межпредметную связь и практическую значимость изученного материала.
Например, изучив материал на проценты в курсе алгебры, учащиеся часто испытывают затруднения при решении аналогичных задач в рамках таких предметов как физика и химия. Таким образом, отработанный алгоритм решения задач на проценты в рамках курса алгебра, не диссеминируется на других предметах.
Практическая значимость алгоритма решения задач на проценты, также остается загадкой для многих учащихся. Несмотря на то, что в будущем в жизни им придется их высчитывать.
Анализируя материал школьных курсов алгебры, геометрии, физики и информатики, можно отметить, что есть целый ряд междисциплинарных тем, в которых учитель-предметник, объясняя материал, может делать акцент на смежные дисциплины, и приводить пример данной модели на примерах другого предмета.
Также в современных учебниках, несмотря на требования ФГОС, до сих пор мало практических задач, которые позволили бы учащимся понять, зачем они изучают тот или иной материал.
Таким образом, межпредметные связи выходят на первый план при оценке учебных достижений учащихся в рамках действия ФГОС [1].
С 2020 года формат заданий в ОГЭ и ЕГЭ также смещается в сторону задач с практическим содержанием.
В первой части учащимся придется ознакомиться с текстом и решить 5 практических задач.
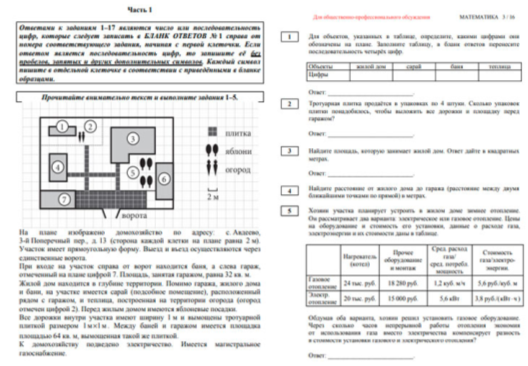
Таким образом, основной акцент делается на умения, а не на знания. Необходимо будет продемонстрировать навыки систематизации информации и аргументации.
Рассмотрим, в качестве примера задачу из курса физики 9 класс:
Высота над землей подброшенного вверх мяча меняется по закону:
h(t) = t2- 5t+6.
Сколько секунд мяч будет находиться на высоте не менее 4 м?
Рассмотрим данную задачу с точки зрения трех выбранных нами предметов:
− Математика (Цель: Изучение свойств квадратичной функции, решение квадратного уравнения, построение графика функции, подготовка к решению заданий ОГЭ)
− Физика (Цель: Изучение закона равноускоренного движения, подготовка к решению заданий ОГЭ)
− Информатика (Цель: Построение графика в программе Excel, создание формулы и таблицы значений функций, подготовка к решению заданий ОГЭ).
Таким образом, у учащегося формируется межпредметная связь в рамках одной темы. При этом каждый предмет в целом достигает различных результатов и целей в процессе решения одной и той же задачи.
Однако, если посмотреть на данную тему через призму трех или двух предметов, то можно повысить уровень усвояемости материала. Например, в рамках урока информатики у преподавателя есть возможность визуализировать данный процесс с помощью программных средств, и показать на уроке статичную и динамическую модель полета мяча. Таким образом, учащиеся наглядно увидят траекторию движения мяча и поймут смысл задачи.
Рассмотрим основные достоинства модульной системы обучения
- структурированность учебного материала (позволяет синхронизировать темы для выстраивания межпредметных связей, повышает качество обучения, позволяет использовать индивидуальные программы обучения)
- формирования компетенций исходя из личностных качеств учащихся;
- возможность адаптация учебного материала к дидактическим условиям, формирование практических навыков решение;
- возможность дистанционного обучения.
В качестве недостатка модульной системы можно выделить существование вероятности неправильной компоновки учебного материала в модулях.
Таким образом, повысить метапредметные результаты можно за счет интеграции модульного изучения школьных предметов, а формирование целостной картины мира в рамках обучения возможно при активном включении практически-ориентированных заданий.
Литература:
- Федеральные государственные образовательные стандарты https://fgos.ru
- Атанасян Л. С., Бутузов В. Ф., Кардомцев С. Б. и др. Геометрия. 7–9 классы: учебник для общеобразовательных учреждений. М.: Просвещение, 2013. 384 с.
- Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. Алгебра: учебник для 9 классов общеобразовательных учреждений. М.: Просвещение, 2012. 271 с.
- Открытый банк заданий ЕГЭ. URL: http://mathege.ru/or/ege/











