Математические задачи как средство формирования исследовательской компетенции у учащихся в классах физико-математического профиля
Автор: Великий Дмитрий Сергеевич
Рубрика: 5. Педагогика общеобразовательной школы
Опубликовано в
Дата публикации: 27.09.2020
Статья просмотрена: 44 раза
Библиографическое описание:
Великий, Д. С. Математические задачи как средство формирования исследовательской компетенции у учащихся в классах физико-математического профиля / Д. С. Великий. — Текст : непосредственный // Образование: прошлое, настоящее и будущее : материалы VIII Междунар. науч. конф. (г. Краснодар, октябрь 2020 г.). — Краснодар : Новация, 2020. — С. 43-46. — URL: https://moluch.ru/conf/ped/archive/379/16040/ (дата обращения: 24.04.2025).
Исследовательская деятельность учащихся на уроке — наиболее прогрессивный способ изучения математики и одна из эффективных форм внеклассной работы по предмету. Приобщение учащихся к исследовательской деятельности способствует самореализации и самосовершенствованию личности учащегося.
Решая исследовательскую задачу, человек познает много нового: знакомится с новой ситуацией, описанной в задаче, с применением математической теории к ее решению, познает новый метод решения или новые теоретические разделы математики, необходимые для решения задачи. Исследовательские задачи создают условия для проявления творческой активности учащегося, выражающейся в стремлении познать объективно новые факты, используя теорию научных исследований. При решении исследовательских задач ученик обучается применять математические знания к практическим нуждам.
На сегодняшний день имеются проблемы в отсутствия системности знаний у учащихся, умения переносить полученные знания на аналогичные или иные ситуации, недостаточной самостоятельности мышления и как следствие, не умения правильно выстраивать этапы исследовательской деятельности. Эти проблемы во многом связаны со слабым использованием в образовательном процессе потенциала внутри предметных связей. Именно при решении определённых заданий интегрируются знания, умения, навыки из:
– математической логики (конъюнкция, дизъюнкция предикатов, отрицание предиката);
– теории множеств: пересечение множеств (решения систем), объединение множеств (решения совокупности), дополнения множеств;
– алгебры (делимость многочленов, разложение на множители, метод неопределенных коэффициентов и др.).
– геометрии (преобразования симметрии, параллельного переноса, и др.), аналитической геометрии (поиск коэффициентов в уравнении линии, условие пересечение линий, взаимного расположении прямых и др.);
– математического анализа (условия монотонности и экстремумов функции, свойства непрерывных функций и др.).
Примером могут служить задачи с параметрами, они как правило, являются хорошим материалом для проведения различного рода исследований. Спецификой задач с параметрами является то, что наряду с неизвестными величинами в них фигурируют параметры, численные значения которых не указаны конкретно, но считаются известными и заданными на некотором числовом множестве. При этом, значения параметров существенно влияют на логический и технический ход решения задачи и форму ответа. Решение задач с параметрами следует проводить с использованием исследовательского характера рассуждений: выделить противоречие и проблему исследования, которое необходимо провести для решения задачи, поставить цель, сформулировать гипотезу исследования, выделить задачи исследования, выбрать методы и провести исследование, сделать вывод (рефлексию).
Задача. Есть ли на графике функции
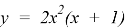
В процессе решения задачи выделите противоречие и проблему исследования, которое необходимо провести для решения задачи, поставьте цель, сформулируйте гипотезу, выделите задачи исследования, выберите методы и проведите исследование. На основании полученных результатов сделайте вывод. Проведите рефлексию завершенного исследования
Основная трудность в решении данной задачи заключается в выяснении аналитической записи условия центральной симметричности графика функции
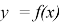
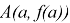
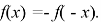
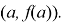
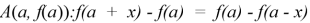
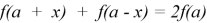
Решать такую задачу с учащимися следует, организуя исследование. Во-первых, выделить противоречие между наличием формулы, выражающей условие центральной симметрии графика нечетной функции относительно начала координат, и незнанием формулы, выражающей условие центральной симметрии графика функции относительно точки с координатами
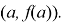
Выявленное противоречие определяет проблему исследования, заключающуюся в нахождении формулы условия центральной симметрии графика функции относительно точки с координатами
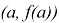
Сформулируем
цель исследования
: составить формулу, выражающую условие центральной симметрии графика функции относительно точки с координатами
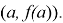
1. Сформулировать определение центральной симметрии, известное нам из геометрии.
2. Сформулировать определение нечетной функции.
3. На основании этих определений сформулировать условие центральной симметрии графика функции относительно точки с координатами
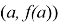
Сформулируем гипотезу исследования: если обобщить определения центральной симметрии относительно точки О и нечетной функции, то мы выявим условия центральной симметрии графика функции относительно точки с координатами
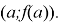
На этапе анализа фабулы задачи целенаправленно прописывать методологический аппарат последующего решения(исследования) задачи помогает учащимся развивать ЗУН по формулированию целей, гипотез. Позволяет сопоставлять желаемый результат с потенциальными возможностями; определить последовательность шагов для достижения цели; сформулировать задачи адекватные разрешению проблемы. Это всё способствует развитию праксиологическому и когнитивному компонентам исследовательской деятельности.
Приступим к решению поставленных задач. Из курса геометрии известно, что центральной симметрией относительно точки О называется отображение плоскости, при котором каждая точка М переходит в точку М', симметричную точке М относительно точки О. Функция
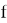
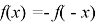
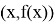
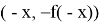
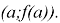
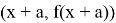
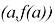
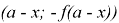
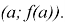

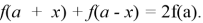
На данном этапе решения задачи ученикам приходится искать теоретический материал для подтверждения выдвинутой гипотезы, проводить математические преобразования. То есть, происходит развитие деятельностного компонента исследовательской компетенции.
Таким образом, мы доказали гипотезу исследования данной задачи и составили формулу, выражающую условие центральной симметрии графика функции относительно точки с координатами
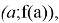
Применим полученное условие к решению задачи. Сумма
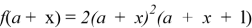
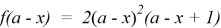
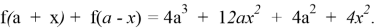
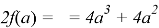
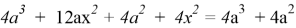
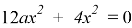
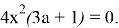
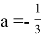
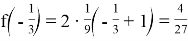
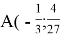
Ответ:
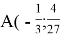
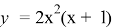
На заключительном этапе решения задачи проводится рефлексия и делаются выводы, что выявленное условие центральной симметрии графика функции относительно точки с координатами
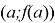
Решение задачи с параметрами, проведенное с применением исследовательского характера рассуждений, позволяет учащимся пройти через основные этапы исследования, что способствует формированию их исследовательской компетенции.
Не следует забывать, что, применяя задачи с практико-ориентированной фабулой, мы так же развиваем исследовательскую компетенцию у учащихся. При решении таких задач мы также проходим все этапы исследования.
Приведём примеры такого задания из школьной темы Производные :
Задача: На лесопильной раме для продольного пиления бревна часто используют метод распиловки его на квадратный брус и четыре продольные линии — доски. Каким образом нужно оптимально расположить пилы для такой распиловки, чтобы издержки производства были минимальным, если имеется бревно диаметром 60см.
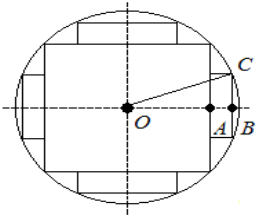
Рис. 1
Из (рис. 1) видно, что для ответа на вопрос задачи достаточно определить толщину выпиливаемых досок. Так как сторона квадрата, вписанного в окружность радиуса
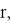
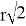
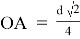
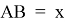
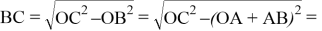
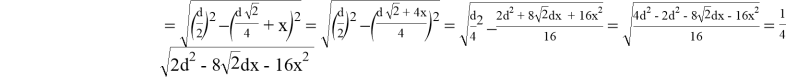
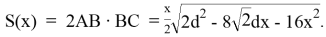
Требуется узнать, при каком
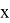
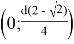
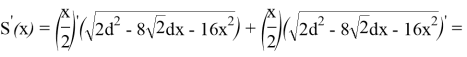
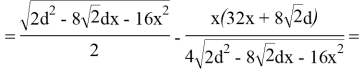
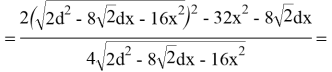
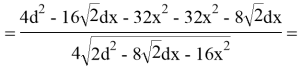
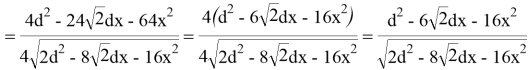
Критическая точка
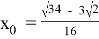
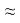
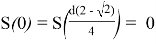
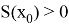
Подставляем имеющиеся значения и получаем, что толщина доски
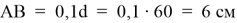
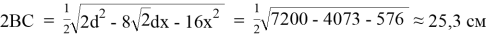
6 см и шириной 25,3 см. Таким образом, площадь доски будет максимальной, а издержки производства минимальными.
Мы знаем, что математика стоит в основе множества сфер человеческой деятельности, будь то естественные науки, экономика, медицина, промышленная или IT-индустрия. Нам как учителям стоит увеличить на уроках применения таких исследовательских заданий. Это позволит обеспечить развития метапредметных компетенций, к каким и относится исследовательская компетенция у учащихся и повысить мотивацию к обучению.











