Интегрированный урок (математика и информатика): решение практикоориентированных задач



Тема урока: Решение практико-ориентированных задач.

Цели урока:

предметные —— формирование навыков применения разных алгоритмических конструкцией для решения задач;

метапредметные — умение анализировать задачу, подбирая математическую модель, способ;

личностные — понимание роли фундаментальных знаний как основы современных информационных технологий.

Планируемые результаты обучения :

Личностные результаты:

Проявление творческого отношения к процессу изучения темы.

— формирование мотивации учения;

— формирование навыков самоорганизации

— формирование математического мышления

— формирование навыков грамотного письма,

— формирования навыков поиска информации в имеющемся источнике.

— формирование навыков решения задач

Метапредметные результаты:

Познавательные результаты:

Умение:

— находить качественные учебные материалы в различных информационных ресурсах;

— прогнозировать учебную ситуацию;

— развитие познавательной активности

— обобщать полученную информацию.

Регулятивные результаты

Умение:

— работать по плану урока;

— формирование осознанного подхода к оценке деятельности.

— умение ставить учебную задачу, называть цель, формулировать тему в соответствии с нормами русского языка;

— умение использовать полученные знания на практике

Коммуникативные результаты

Умение:

— аргументировать свою позицию и высказывать ее в ходе коллективного обсуждения;

— адекватно использовать речевые средства, давать оценку своим действиям, оценивать результат;

— развитие навыков общения со сверстниками и взрослыми в процессе деятельности.

— согласовывать позиции и находить общее решение учебной ситуации.

Формы работы учащихся: фронтальная, парная, индивидуальная

Этапы урока	Материал ведения урока	Деятельность учащихся	УУД на этапах урока
Организационный момент	Проводим необычное занятие. Урок математики, информатик по теме «Решение практикоориентированных задач» Для проведения занятия каждая группа выберет науку, по которой будет решать задачу 4 листа разного цвета. Выбирают Желтый –география Зеленый биология Красный физика Синий химия Науку озвучили Каждая группа получила задачу из естественнонаучного цикла. Как связать эти 4 задачи из разных областей с математикой и информатикой? ОТВЕТЫ Попробуем сформулировать цель урока Цель: показать на практике применение информатики и математики для решения задач естественно-математического цикла	Дети рассаживаются по местам. Проверяют наличие принадлежностей. Проходит жеребьевка по задачам. Ребята пытаются самостоятельно сформулировать цель урока.	Личностные УУД: — формирование навыков самоорганизации
Актуализация	Ребята давайте повторим нужный для работы материал. Математика: (Приложение: слайды 4–7) Перейдем к повторению материала по информатике. Информатика: (Приложение: слайды 8–10)	Ребята повторяют основной материал необходимый для решения задач с точки зрения математики и информатики.
Объяснение хода работы	Ребята мы с вами повторили материал и переходим к решению задач. Обратите внимание на слайд (приложение, слайд 11). Каждая группа работает по плану. Для достижения целей необходимо решить задачи – Составить мат. Модель – Написать программу – Оформить результат работы в презентации – Представить работу. Группа состоит из математика, программиста и аналитика. Математик составляет математическую модель, программист пишет программу, аналитик собирает информацию в презентацию и представляет результат работы. На работу вам дается 20 минут (Если в работе затруднения, то любой результат в презентацию пишем)	Обучающиеся в группах знакомятся с планом работы и приступают к разбору полученных задач.	Регулятивные УУД: — формирование осознанного подхода к оценке деятельности.
Практическая часть	Физкультминутка. Зарядка для глаз: Глазами влево –вправо(5 раз), вверх-вниз(5 раз), нарисовать глазами восьмерку. Работа по группам по плану Группа состоит из математика, программиста и аналитик. Каждый выполняет свои функции. Математик составляет мат. Модель, информатик программирует в python, аналитик — собирает информацию в презентацию (яндекс.диск) представляет результат работы	Обучающиеся в группах начинают решать задачи, составляют математическую модель (математик в группе), программируют (программист в группе), собирают информацию в презентацию на Яндекс диске. Представляют свою работу для оценивания.	Коммуникативные УУД: — развитие навыков общения со сверстниками и взрослыми в процессе деятельности. Личностные УУД: — формирование математического мышления Регулятивные УУД: — умение ставить учебную задачу, называть цель, формулировать тему в соответствии с нормами русского языка,
Представление результатов работы (10 мин)	Перейдем к представлению ваших работ. Во время представления работы каждая группа оценивает работу ребят. Открываете оценочный лист в Яндекс таблице и ставите 1, если все хорошо, и 0, если что-то пошло не так. Ребята, спасибо, за вашу работу. По таблице видно, что все справились со своей задачей.	Ребята — аналитики с каждой группы выходят защищать работу группы, остальные участники заполняют оценочные листы.	Познавательные УУД: — развитие познавательной активности Личностные УУД: — формирование навыков грамотного письма, формирования навыков поиска информации в имеющемся источнике. Познавательные УУД: — развитие познавательной активности Личностные УУД: — формирование навыков решения задач Регулятивные УУД: — умение использовать полученные знания на практике
Итоги урока, выставление оценок.	Подведем итоги нашего занятия. Послушайте пословицу «Умение везде найдет применение». Как вы соотнесете эту пословицу с тем, что вы выполняли на уроке? Д/З: Придумать задачу по своей науке. Рефлексия: Выберете фразеологизм, который характеризует вашу работу на уроке: Шевелить мозгами Краем уха Хлопать ушами Спасибо за урок!	Подводят с учителями итоги урока, анализируют полученный результат.

Приложение 1

Задачи к уроку:

Химия

Сергей Петрович решил построить на дачном участке теплицу. Он хочет удобрить почву в теплице, для этого ему нужно получить раствор в количестве 10 л на всю теплицу , содержащий не более 25 % удобрений в растворе. Сергей Петрович в наличии имеет только 4 литра 15-процентного водного раствора удобрений и 6 литров 25-процентного водного раствора этих же удобрений. Сколько процентов удобрений будет содержать новый раствор? Смешав их, получит ли он раствор , содержащий не более 25 % удобрений в растворе.

с

Физика

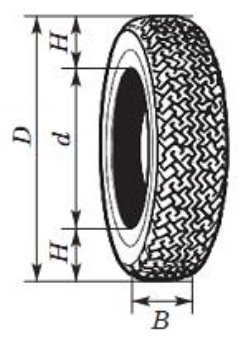
Для маркировки автомобильных шин применяется единая система обозначений 225/60 R18 . Первое число означает ширину В шины (ширину протектора) в миллиметрах. Второе число — высота боковины Н в процентах к ширине шины ( Н = 0,6В .) Последующая буква означает конструкцию шины. Например, буква R значит, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса в дюймах ( в одном дюйме 25,4 мм ). По сути, это диаметр d — внутреннего отверстия в шине. Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины.

Завод производит автомобили и устанавливает на них шины с маркировкой: 225/60 R18. Завод допускает установку шин с другими маркировками.

На сколько изменится пробег (длина окружности колеса) автомобиля при одном обороте колеса , если заменить колёса, установленные на заводе, колёсами с шинами маркировки 215/60 R18 ? Результат округлите до десятых.

География

В горных районах, особенно в южных широтах с влажным климатом, земледельцы на склонах гор устраивают террасы. Земледельческие террасы — это горизонтальные площадки, напоминающие ступени. Во время дождя вода стекает с верхних террас вниз по специальным каналам. Поэтому почва на террасах не размывается и урожай не страдает. Медленный сток воды с вершины склона вниз с террасы на террасу позволяет выращивать даже влаголюбивые культуры. В Юго-Восточной Азии террасное земледелие широко применяется для производства риса, а в Средиземноморье — для выращивания винограда и оливковых деревьев. Возделывание культур на террасах повышает урожайность, но требует тяжелого ручного труда.

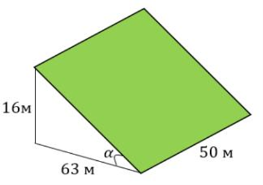
Земледелец владеет несколькими участками, один из которых расположен на склоне холма. Ширина участка 50 м, а верхняя точка находится на высоте 16 м от подножия.

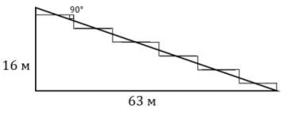
Земледелец решил устроить террасы на своем участке (см. рисунок ниже), чтобы выращивать рис, пшено и кукурузу. Строительство террас возможно, если угол склона (уклон) не больше 50 % (тангенс угла склона α, умноженный на 100 %). Удовлетворяет ли склон холма этим требованиям? Сколько процентов составляет уклон? Ответ округлите до десятых.

Биология

Известно, что бактерии размножаются делением: одна бактерия делится на две; каждая из этих двух в свою очередь тоже делится на две, и получаются четыре бактерии; из этих четырех в результате деления получаются восемь бактерий и т. д. Результат каждого удвоения будем называть поколением.

Бактерия, попав в живой организм, к концу 20-й минуты делится на две бактерии, каждая из них к концу следующих 20 минут делится опять на две и т. д. Найдите число бактерий, образующихся из одной бактерии к концу суток. (В сутках 1440 минут)

Литература:

1. Алгебра. 9 класс: учеб, для общеобразоват. организаций. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; под ред. С. А. Теляковского. — 21-е изд. 2014. — 271 с.
2. Боряк, Е. А. Формирование регулятивных УУД на уроках алгебры при реализации личностного подхода в условиях подготовки к итоговой государственной аттестации / Е. А. Боряк, В. Н. Фрундин. — Текст: непосредственный // Актуальные проблемы теории и практики обучения математике, информатике и физике в современном образовательном пространстве. — Курск: Сборник статей, 2018. — С. 114–119.
3. Тренировочные варианты. — Текст: электронный // Решу ОГЭ: [сайт]. — URL: https://math-oge.sdamgia.ru/ (дата обращения: 4.05.2023).