Статистическое моделирование на ЭВМ дискретных случайных величин средствами языка программирования R



В статье рассматривается моделирование случайных величин, вычисление параметров случайных величин по выборке и изучение свойства состоятельности выборочных оценок средствами языка программирования «R».

Ключевые слова: моделирование, случайная величина, язык R.

Пользуясь средствами языка программирования «R«, рассмотрим процесс реализации на ЭВМ и исследования на точность алгоритма моделирования случайной величины, распределенной по геометрическому закону G(p):

(1)

где — заданный параметр распределения.

Дискретная случайная величина (ДСВ) ξ с геометрическим законом распределения есть число испытаний Бернулли до первого успеха (включая первый успех), если вероятность успеха в каждом испытании равна р [1, с. 22].

Метод моделирования ДСВ ξ с законом распределения G(p) основан на следующей теореме [2, c. 55]:

Теорема. Если R — биномиальная случайная величина (БСВ), то случайная величина

(2)

где [z] — целая часть z, имеет распределение (1).

Реализуем на языке программирования «R» моделирование n независимых случайных чисел, имеющих геометрическое распределение:

> n = 100; # количество независимых случайных чисел

> p = 0.5; # заданный параметр распределения

> eta = с( ); # вектор независимых случайных чисел

> geo = function(n, p) # функция для моделирования случайной величины

+ { R = runif(n);

+ for (i in 1:n) { eta[i] <- floor( log( R[i] ) / log( 1 - p ) ); }

+ return (eta);}

> ksi = geo(n,p); # моделирование случайной величины

Построим полигон относительных частот и полигон распределения

вероятностей при различных объемах выборок (n = 100, n = 1000, n = 10000). Для решения данной задачи используем следующий программный код:

> n1= table(ksi); # распределение частот случайных величин

> otn = n1/n; # распределение относительных частот

> plot(otn, "b", pch=19, col="red", xlab="Случайная величина",ylab="Относительная частота", lty=1); # графическое отображение

> x <- (min(ksi):max(ksi)); # вектор независимых случайных чисел

> y <- dgeom(x,p); # вектор теоретической плотности распределения

> lines(x,y,"b", pch=19,col="blue", lty=2);

Графические результаты приведены на рис. 1–3. На их основании можно утверждать, что с увеличением объёма выборки график полигона относительных частот стремится к полигону распределения вероятностей.

Аналогично с увеличением объема выборки, график эмпирической функции распределения также стремится к теоретической функции распределения. Графический результат для объёма выборки n = 10000 приведён на рис. 4.

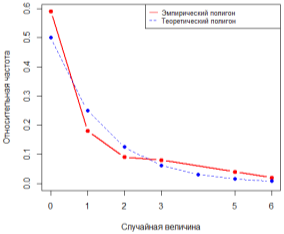
Рис. 1. Графики полигона относительных частот и теоретического полигона распределения вероятностей, n=100

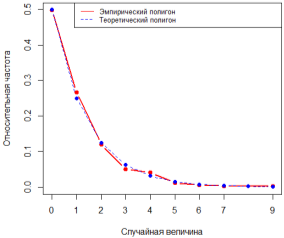
Рис. 2. Графики полигона относительных частот и теоретического полигона распределения вероятностей, n=1000

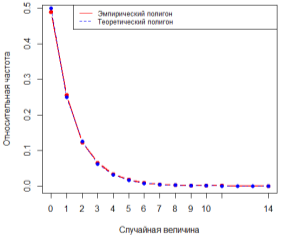
Рис. 3. Графики полигона относительных частот и теоретического полигона распределения вероятностей, n=10000

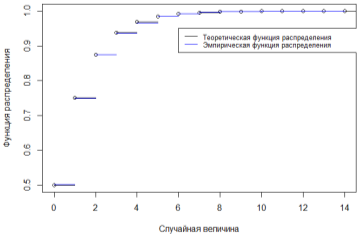
Рис. 4. Графики теоретической и эмпирической функции распределения, n=15000

Для построения графиков эмпирической и теоретической функций распределения используем следующий программный код:

> y1 <- pgeom(x,p); # вектор теоретической функции распределения

> plot(x, y1, col="black", xlab="Случайная величина", ylab="Функция распределения"); # графическое отображение

> for(i in (min(ksi):max(ksi)))

+ { y <- pgeom(i,p); lines(c(i,i+1),c(y,y),"l")}

> k <- 0; for (i in (min(ksi):max(ksi)))

+{x11<-c(i:(i+1)); k<-k+otn[i+1]; y11<-c(k,k); lines(x11,y11,col="blue");}

Будем использовать следующий программный код для вычисления теоретических и выборочных математического ожидания и дисперсии:

> vmo = mean(ksi); # выборочное мат. ожидание

> mteor = (1-p)/p; # теоретическое мат. ожидание

> vd = var(ksi); # выборочная дисперсия

> dteor = (1 - p) / ( p*p ); # теоретическая дисперсия

Чтобы убедиться в состоятельности выборочной оценки математического ожидания, реализуем средствами языка программирования «R» решение следующих задач: построить график стремления выборочной оценки параметра распределения к параметру распределения по вероятности с увеличением объема выборки n; построить линию параметра; построить доверительные границы, используя неравенство Чебышева. Реализацию решения выполняет следующий программный код:

> mx<-c(); for (j in (1:n)) { mx[j]=mean(rgeom(j,p)); }

> plot((1:n), mx, 'l', xlab='n', ylab='выборочное среднее');

> a1=c(1,n);b1=c(mteor, mteor); lines(a1,b1, col='red');

>pu=mteor+sqrt((1-p)/((1:n)*(p*p)*(1-0.95))); lines((1:n), pu, col='green');

>pu=mteor-sqrt((1-p)/((1:n)*(p*p)*(1-0.95))); lines((1:n), pu, col='green');

Графический результат для объёма выборки n = 15000 приведён на рис. 5. На его основании можно утверждать, что с увеличением объёма выборки выборочная оценка математического ожидания стремится по вероятности к теоретическому математическому ожиданию распределения.

Для реализации решения задачи статистического моделирования на ЭВМ дискретных случайных величин средствами языка программирования «R» на примере геометрического распределения были использованы следующие встроенные функции языка:

– runif(n) — моделирование n равномерно распределенных случайных величин от 0 до 1;

– floor(x) — служит для возврата целой части числа x;

– log(x) — вычисление натурального логарифма числа x;

– sqrt(x) — вычисление квадратного корня числа x;

– mean(x) — вычисление математического ожидания вектора х;

– var(x) — вычисление дисперсии вектора x;

– dgeom(x,p) — вычисление теоретической плотности распределения;

– pgeom(x,p) — вычисление теоретической функции распределения;

– rgeom(n,p) — моделирование n независимых случайных величин, распределенных по геометрическому закону.

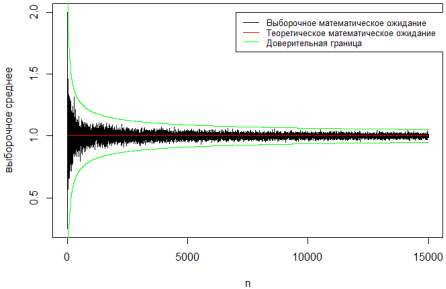
Рис. 5. График сходимости выборочной оценки к параметру распределения, n=15000.

Литература:

1. Лобач В. И. Имитационное и статистическое моделирование: Практикум для студентов мат. и экон. спец. / В. И. Лобач, В. П. Кирлица, В. И. Малюгин, С. Н. Сталевская. — Минск: БГУ, 2004. — 189 с.
2. Харин Ю. С., Степанова М. Д. Практикум на ЭВМ по математической статистике. — Минск: Университетское, 1987. — 304 с.
3. Хастингс Н., Пикок Дж. Справочник по статистическим распределениям. — М.: Статистика, 1980. — 95 с.