Оценка показателей надежности испытаний при экспоненциальном законе распределения отказов



В статье проведена оценка показателей надежности безотказной работы системы. На примере показан расчет основных показателей средствами VBA.

Ключевые слова: безотказная работа, доверительный интервал, испытания, число отказов, экспоненциальный закон.

Проведение испытаний новых изделий или системы организуется в соответствии с планом, в котором указывается: количество испытуемых изделий ( N ), будут ли заменяться отказавшие изделия ( B ) и когда испытания необходимо прекратить (прекращение испытаний после истечения Т часов или прекращение испытаний при возникновении r — го отказа).

Экспоненциальный закон представляет собой постоянную интенсивность отказов, т. к. определяется параметром λ- const при δ =1 .

, интенсивность отказов λ(t) ≡ λ . (1)

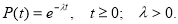
Если указано время работы каждого изделия от начала работы до его отказа, расчет суммарной наработки всех элементов S Б( r ) и S Б( Т ) вычисляется с использованием выражения (2).

(2)

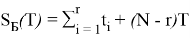
Среднее время безотказной работы — T _ср при экспоненциальном законе распределения равно величине, обратной ИО — 1/ λ , т. е.:

(3)

-плотность распределения наработки(4)

= ∙(-ln

).

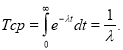
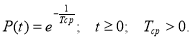
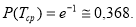
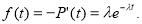
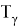
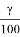
Вероятность восстановления P _B ( t ):

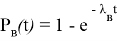
Дисперсия времени безотказной работы:

(5)

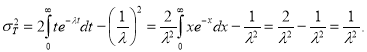
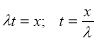
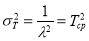
Условная вероятность безотказной работы устройства на интервале времени t , после того как оно безотказно проработало на интервале τ .

(6)

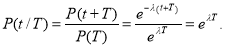
Под доверительным интервалом понимается диапазон значений параметра, в пределах которого с некоторой вероятностью γ может находиться его истинное значение. Вероятность γ называется доверительной вероятностью или коэффициентом доверия. Для экспоненциального закона распределения отказов при плане испытаний N , Б, r установлено, что величина U = 2 S _Б ( r )λ подчиняется χ ² — распределению с 2 r степенями свободы, где S _Б ( r ) — суммарная наработка изделий, установленных на испытание (может быть определена из выражения (7), λ — истинное значение интенсивности отказа, r — число отказов (или разрядов, если отказы сгруппированы по разрядам) [1].

(7)

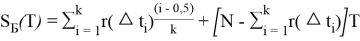
Вероятность того, что величина U находится в пределах χ ² ₁ и χ ² ₂ , равна

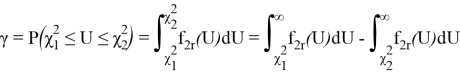
Интеграл табулирован. Поэтому, задавшись значениями λ _min и λ _max и зная из обработки результатов эксперимента суммарную наработку S _Б ( r ), находим χ ² ₁ и χ ² ₂ и по таблице квантилей распределения χ ² –квадрат находим коэффициент доверия γ.

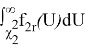
Квантилем случайной величиныχ называется такое значение случайной величины х _р , для которого с вероятностью 1– р можно утверждать, что полученное значение этой случайной величины попадет в интервал (–∞, х _р ).

Однако чаще стоит обратная задача: по коэффициенту доверия γ и суммарной наработке изделий при испытании S Б( r ) требуется найти λmin и λmax.

Установлено, что доверительный интервал будет минимальным, если площади под кривой плотности распределения f _{2 r} в интервалах [0, χ ² ₁ ] и [χ ² ₂ , ∞] равны.

Тогда значения χ ² ₁ и χ ² ₂ ограничивают соответственно площади 0,5(1+γ) и 0,5(1 — γ).

Последовательность определения доверительных интервалов сводится к следующему. Задавшись коэффициентом доверия γ, определяем 0,5(1+γ) и 0,5(1 — γ) и, зная число степеней свободы 2 r , по таблице квантилей χ ² – распределения находим значения χ ² ₁ и χ ² ₂ . Доверительные оценки λ _min и λ _max могут быть определены из неравенства

(8)

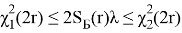
Отсюда найдем

(9)

(10)

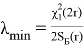
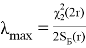
Рассмотрим пример расчета показателей, полученных при испытании 100 изделий (из строя вышло 34). Испытания были прекращены после истечения 100 часов.

Для построения статистического ряда время испытаний разобьем на равные интервалы (разряды) продолжительностью 10 часов и для каждого разряда проведем расчет.

Поскольку за время испытания отказало 34 % изделий, оценка интенсивности отказов подсчитывалась с использованием выражений для плана N , Б , Т.

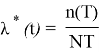
Доверительные границы:

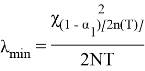
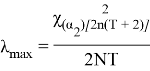
0,2

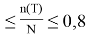
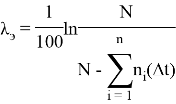
Частота отказов определялась для каждого разряда из выражения

.

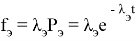
f э, λэ, Q э( t ) — параметры потока отказов при экспоненциальном законе распределения [1, 2].

Вероятность отказа подсчитывалась по формуле

.

Листинг программы расчета показателей при экспоненциальном законе распределения:

'Вычислим 1 строку таблицы(3)============================= t

Строка = 3

For СтолбецТаблицы = 4 To КоличествоСтолбцовТаблицы + 3

Sheets("ОсновнаяТаблица").Cells(Строка, СтолбецТаблицы).Value = Sheets("ОсновнаяТаблица").Cells(Строка - 1, СтолбецТаблицы).Value * ВременнойИнтервал

Next

'Вычислим 2 строку таблицы(4)============================= n*

n = 0 'количество вышедших из строя элементов в периоде

СтрокаДанных = 4

СтрокаТаблицы = 4

СтолбецТаблицы = 4

КонтрольноеЗначениеВременногоИнтервала = ВременнойИнтервал

While Sheets("Исходные данные").Cells(СтрокаДанных, 1).Value <> ""

If КонтрольноеЗначениеВременногоИнтервала > ОбщееКоличествоЧасов Then GoTo конец

If Sheets("Исходные данные").Cells(СтрокаДанных, 1).Value <= КонтрольноеЗначениеВременногоИнтервала Then

n = n + 1

Else

Sheets("ОсновнаяТаблица").Cells(СтрокаТаблицы, СтолбецТаблицы).Value = n

КонтрольноеЗначениеВременногоИнтервала = КонтрольноеЗначениеВременногоИнтервала + ВременнойИнтервал

СтрокаДанных = СтрокаДанных - 1

СтолбецТаблицы = СтолбецТаблицы + 1

n = 0

End If

СтрокаДанных = СтрокаДанных + 1

Wend

If n <> 0 Then Sheets("ОсновнаяТаблица").Cells(СтрокаТаблицы, СтолбецТаблицы).Value = n

конец:

'Вычислим 7 строку таблицы(9)=============================ЛямбдаЭ x 10^3

СтрокаТаблицы = 9

СтолбецТаблицы = 4

СуммаВышедшихЗаВсеВремя = 0

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы - 1)

СуммаВышедшихЗаВсеВремя = СуммаВышедшихЗаВсеВремя + Sheets("ОсновнаяТаблица").Cells(4, n).Value

Next

СтолбецТаблицы = 4

Sheets("ОсновнаяТаблица").Cells(СтрокаТаблицы, СтолбецТаблицы).Value = Round((1 / 100 * Log(КоличествоЭлементов / (КоличествоЭлементов - СуммаВышедшихЗаВсеВремя))) * 1000, 2)

Sheets("ОсновнаяТаблица").Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n - 1)).MergeCells = True

Sheets("ОсновнаяТаблица").Range(Cells(СтрокаТаблицы, 4), Cells(СтрокаТаблицы, n - 1)).HorizontalAlignment = xlCenter

'Вычислим 8 строку таблицы(10)=============================fэ х 10^3

СтрокаТаблицы = 10

СтолбецТаблицы = 4

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы - 1)

Sheets("ОсновнаяТаблица").Cells(СтрокаТаблицы, n).Value = Round(((Sheets("ОсновнаяТаблица").Cells(9, СтолбецТаблицы).Value / 1000) * Exp(-Sheets("ОсновнаяТаблица").Cells(2, n).Value / 1000 * Sheets("ОсновнаяТаблица").Cells(9, СтолбецТаблицы).Value * ВременнойИнтервал) * 1000), 2)

Next

'Вычислим 9 строку таблицы(11)=============================Рэ

СтрокаТаблицы = 11

СтолбецТаблицы = 4

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы - 1)

Sheets("ОсновнаяТаблица").Cells(СтрокаТаблицы, n).Value = Round(Exp(-Sheets("ОсновнаяТаблица").Cells(9, СтолбецТаблицы).Value * Sheets("ОсновнаяТаблица").Cells(3, n).Value / 1000), 2)

Next

'Вычислим 10 строку таблицы(12)=============================Qэ(t)

СтрокаТаблицы = 12

СтолбецТаблицы = 4

For n = СтолбецТаблицы To (КоличествоСтолбцовТаблицы + СтолбецТаблицы - 1)

Sheets("ОсновнаяТаблица").Cells(СтрокаТаблицы, n).Value = 1 - Sheets("ОсновнаяТаблица").Cells(11, n).Value

Next

Результаты вычислений представлены в таблице Excel (Таблица 1).

Таблица 1

Результаты расчета основных показателей испытаний

Параметр	Разряды
	1	2	3	4	5	6	7	8	9	10
t	10	20	30	40	50	60	70	80	90	100
n*	5	3	5	2	2	3	3	3	5	3
λэ	4,16
fэ	3,99	3,83	3,67	3,52	3,38	3,24	3,11	2,98	2,86	2,74
Рэ	0,96	0,92	0,88	0,85	0,81	0,78	0,75	0,72	0,69	0,66
Qэ	0,04	0,08	0,12	0,15	0,19	0,22	0,25	0,28	0,31	0,34

Для определения доверительных интервалов при экспоненциальном законе распределения по таблице квантилей χ ² — квадрат распределений. найдем (20) и (20) [3]:

,

.

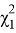
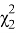
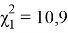
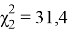
Результаты расчета fэ(t) представлены на рис 1.

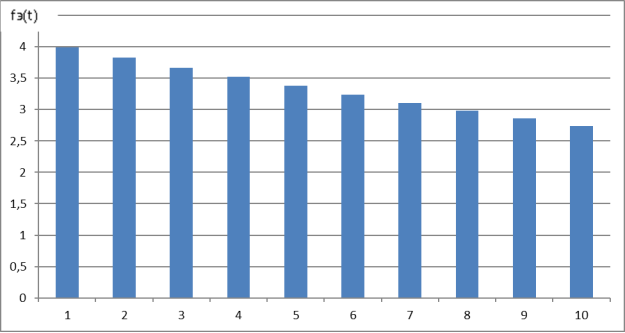
Рис. 1. Гистограмма частоты отказов при экспоненциальном законе распределения

Поскольку в задаче задано время работы каждого изделия до отказа, суммарная наработка всех изделий S _Б ( T ) подсчитывается по формуле (11)

S _Б ( T ) = (11)

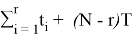
S _Б ( T ) = 8276 ч.

Литература:

1. Коваленко, В. Н., Новиков, А. А. Надежность устройств железнодорожной автоматики, телемеханики и связи. учеб. пособие. — Екатеринбург: УрГУПС, 1995. — с. 78.
2. Основы теории надежности автоматических систем управления: учеб. пособие для вузов / Л. П. Глазунов, В. П. Грабовецкий, О. В. Щербаков. — Л.: Энергоатомиздат, Ленинградское отд-ние, 1984. — 208 с.
3. Бронштейн И. Н., Семендяев К. А. Справочник по математике для инженеров и учащихся ВТУЗов. — М.: Наука, 1980. — 976 с.