Устойчивость сферической оболочки в нестационарном магнитном поле



В работе, на основе рассмотренной в [1] задачи динамической устойчивости сверхпроводящей замкнутой упругой сферической оболочки в однородном магнитном поле, получены области динамической устойчивости рассматриваемой оболочки и настроены графики зависимостей.

Ключевые слова: нестационарное магнитное поле, устойчивость

Введение: На основе выведенных основных уравнений и поверхностных условий, описывающие поведение сверхпроводящих замкнутых сферических оболочек в неоднородном магнитном поле, изучены возможности потери устойчивости оболочки под влиянием переменного магнитного поля и определены критические значения задачи.

Мат. модель задачи и методы решения: Рассмотрена задача динамической устойчивости сверхпроводящей замкнутой упругой сферической оболочки в однородном магнитном поле [1]

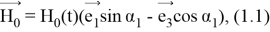
где единичные векторы по направлениям .

Добавочное магнитное поле

, обусловленное экранирующими токами, определяется из решения следующей граничной для уравнений Максвелла задачи

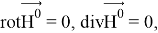
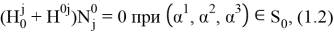
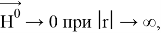
где единичный вектор внешней нормали к недеформированной поверхности тела.

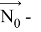
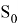
Таким образом,

представляется в виде

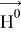
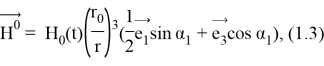
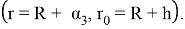
Невозмущенное магнитное поле во внутренней области равно нулю, а во внешней области является результатом наложения полей (1.1) и (1.3). Следовательно

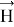
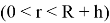
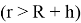
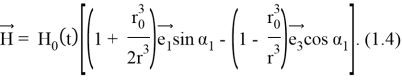
Подставляя (1.4) в систему

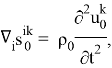
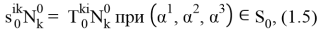
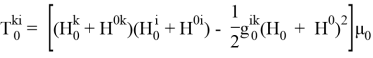
определяем поверхностную силу магнитного происхождения, действующую на оболочку в невозмущенном состоянии, используя (1.5), для отличных от нуля усилий невозмущенного состояния получаем следующие выражения:

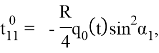
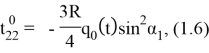
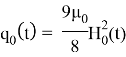
Определение индуцированного во внешней области магнитного поля сводится к решению внешней задачи Неймана для сферы при следующем граничном условии

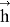
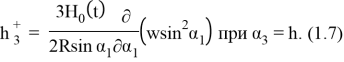
Решение указанной задачи Неймана определяется формулой Бьеркеса и имеет вид [1]

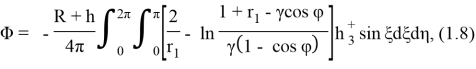
где

,

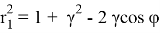
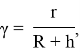
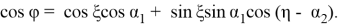
Используя (1.8) определяем и входящие в уравнения устойчивости

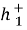
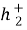
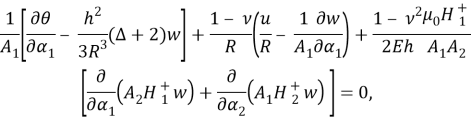
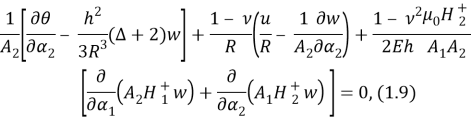
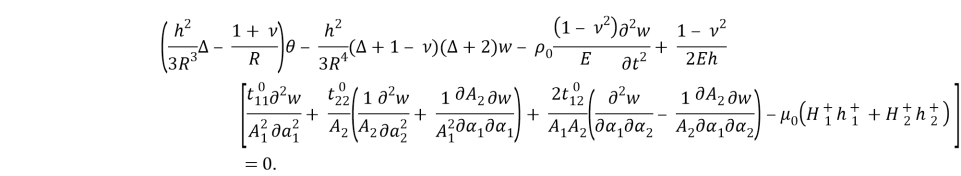
Здесь

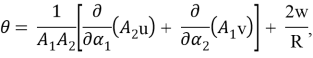
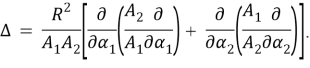
Остается подставить (1.4), (1.6) и найденные изложенным способом значения и

в уравнения (1.9). В результате, исключая функции и , рассматриваемая задача динамической устойчивости сводится к исследованию следующего интегро-дифференциального уравнения относительно :

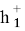
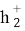
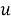
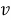
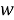
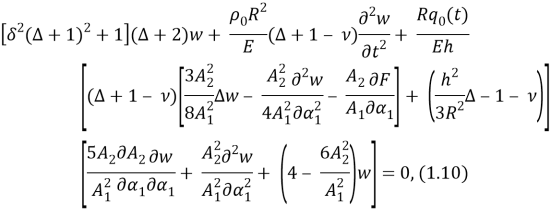
где

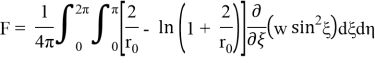
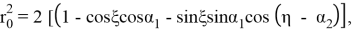
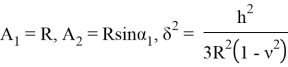
Решение уравнения (1.10), удовлетворяющее граничным условиям, представим в виде

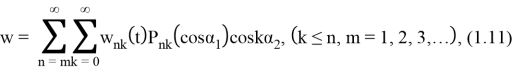
где функции Лежандра.

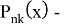
Подставляя (1.11) в уравнение (1.10) и используя процесс ортогонализации, для определения получим бесконечную систему обыкновенных линейных дифференциальных уравнений с переменными коэффициентами. В первом приближении получается следующее уравнение:

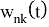
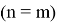
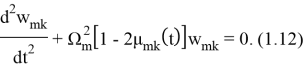
Здесь

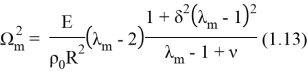
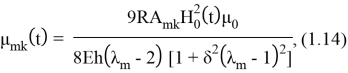
где

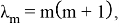
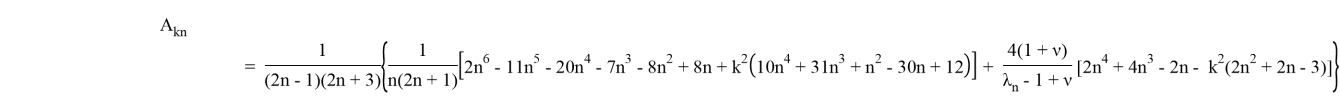
Рассмотрим случай . Тогда уравнение (1.12), в силу (1.13) и (1.14), принимает вид

(1.15)

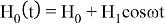
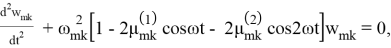
где

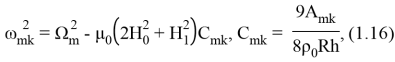
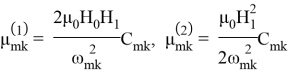
В (1.16) частоты поперечных колебаний оболочки в присутсвии постоянного магнитного поля;

и коэффициенты возбуждения, обусловленные нестационарной частью магнитного поля.

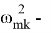
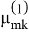
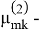
Статическая неустойчивость: Если оболочка находится в постоянном магнитном поле , то, как видно из (1.16) и условием устойчивости является уравнение . Из этого уравнения, используя (1.16), условие устойчивости оболочки можно представить в виде

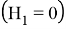
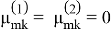
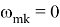
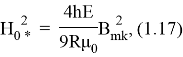
где

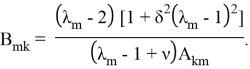
Критическое значение находим из условия минимума функции (1.17) по числам волн и . В результате получим

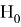
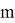
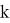
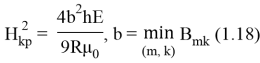
Динамическая неустойчивость: Уравнение (1.15) представляет собой известное уравнение Матье-Хилла [2]. Его решение может быть неустойчивым, устойчивым или периодическим в зависимости от значений параметров и . Границы областей главного параметрического резонанса, согласно [2], определяются по формулам:

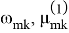
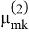
для области, расположенной вблизи частоты

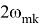
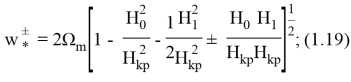
для области, расположенной вблизи частоты

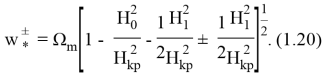
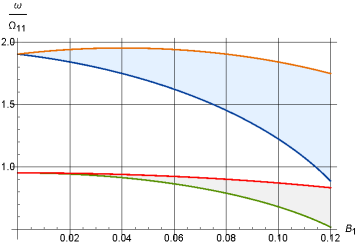
Используя формулы (1.19)-(1.20) легко определить критические параметры напряженности внешнего магнитного поля, под действием которого или происходит потеря статической устойчивости оболочки, или в оболочке возбуждаются резонансные колебания параметрического типа.

Литература:

1. Baghdasaryan G., Mikilyan M. Effects of Magnetoelastic Interactions in Conductive Plates and Shells. Springer, ISBN 978–3-319–19161–4, 2016, -289p.
2. Mikilyan M., Marzocca P. Dynamic instability of of electroconductive cylindrical shell in a magnetic field. International Journal of Solids and Structures, 2018, 160, 168–179.