Дополнительные теоремы о свойствах индекса оператора
Автор: Акопян Александр Рубенович
Рубрика: 1. Математика
Опубликовано в
XIV международная научная конференция «Исследования молодых ученых» (Казань, ноябрь 2020)
Дата публикации: 03.11.2020
Статья просмотрена: 83 раза
Библиографическое описание:
Акопян, А. Р. Дополнительные теоремы о свойствах индекса оператора / А. Р. Акопян. — Текст : непосредственный // Исследования молодых ученых : материалы XIV Междунар. науч. конф. (г. Казань, ноябрь 2020 г.). — Казань : Молодой ученый, 2020. — С. 1-5. — URL: https://moluch.ru/conf/stud/archive/382/16137/ (дата обращения: 24.04.2025).
В данной статье рассмотрены основные и дополнительные теоремы об индексе оператора и дефектных числах, которые имеют большое теоретическое значение в изучении дифференциальных и операторных уравнений.
Ключевые слова: оператор, индекс.
Обозначения и основные теоремы
Пусть имеем банаховы пространства
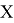
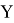

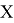
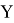

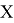

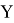
Оператор




Оператор


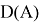

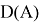



Оператор

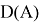
Оператор

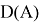
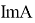
Теорема 1.
Оператор

Теорема 2.
Оператор


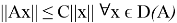
Нормой ограниченного օператора


Под суммой двух операторов



Теорема 3.

Пусть оператор

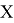
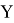
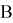
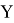
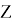

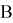
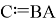
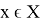
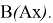
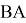
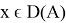
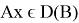
Теорема 4.

Оператор



имеет единственное решение, а оператор
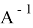
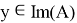
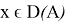

Теорема 5.
Если линейный оператор

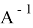
Теорема 6 (Теорема Банаха об обратном).
Если оператор

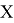
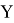

Линейным функционалом над линейным пространством
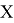


Сопряженным пространством линейного пространства
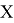
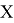

Сопряженным оператором линейного оператора



Легко заметить, что сопряженный оператор также линеен.
Теорема 7.
Если

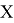
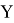

Ядром оператора


Легко заметить, что ядро линейного оператора является линейным подпространством линейного пространства
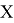
Ядро сопряженного оператора

Если размерность ядра и коядра оператора


А пара


Если оба из этих чисел конечны, то говорят, что оператор обладает конечной d-характеристикой.
Теорема 8.
Коядро конечномерно тогда и только тогда, когда конечномерно фактор пространство


Линейным аннигилятором подпространства

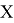

Заметим, что если



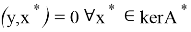

Оператор


Теорема 9.
Оператор

Доказательство:
Пусть оператор



Докажем, что





Пусть теперь образ оператора





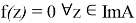


Таким образом теорема доказана!
Оператор




Оператор

-

-

-

Индексом оператора


Заметим также, что оператор

Оператор

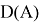
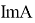
Теоремы о дефектных числах и индекса оператора
Теорема 1.
Пусть




Доказательство:
Пусть


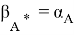

Теорема доказана!
Теорема 2.
Пусть

1. Если


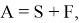
где


2. Если
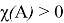

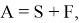
где


3. Если


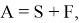
где


Доказательство:
Пусть



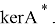

Согласно теореме Хана-Банаха, существуют такие непрерывные линейные функционалы



Обозначим



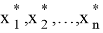

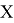


Рассмотрим теперь указанные 3 случая.
1. Если





однозначным образом, где



и рассмотрим оператор





2. Если
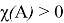


Аналогично предыдущему случаю, оператор


3. Если
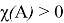
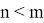
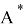
Таким образом, теорема доказана!
Заметим также, что во всех трех случаях оператор

Для следующей теоремы нам понадобится лемма.
Лемма
. Псуть
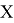

Где
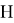

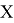
1.


2. Пространство
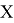

Где

Доказательство:
Пусть

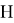


и

Пусть
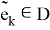
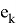

отличен от нуля.
Возьмем




Обозначим

Так как определитель вышеуказанной матрицы отличен от нуля, то можем подобрать



Так как


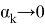



Обозначим


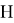


Лемма доказана!
Теорема 3.
Если

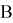
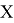
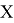


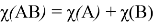
Доказательство:
Обозначим







Где


В силу доказанной леммы


Где

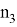
Таким образом


Литература:
- The Index of Elliptic Systems of Singular Integral Operators* R. T. SEELEY JOURNAL OF MATHEMATICAL ANALYSIS AND APPLICATIONS 7, 289–309 (1963)
- И. Ц. Гохберг, М. Г. Крейн, Основные положения о дефектных числах, корневых числах и индексах линейных операторов, УМН, 1957, том 12, выпуск 2(74), 43–118
- А. И. Вольперт, Об индексе и нормальной разрешимости граничных задач для эллиптических систем дифференциальных уравнений на плоскости, Тр. ММО, 1961, том 10, 41–87
- А. Н. Колмогоров, С. В. Фомин, Элементы теории функций и функционального анализа
Похожие статьи
Эффективные методы расчета спектральных задач для самосопряженных операторов
В статье обсуждается теория самосопряженных операторов. Описаны основные определения самосопряженных операторов, их связь с нормальными операторами и спектральные свойства. Кроме того, были рассмотрены классификация самосопряженных операторов и поня...
Приложения символов Ландау
Символы Ландау имеют широкий спектр приложений в области математического анализа, функционального анализа и математической физики. Ниже мы рассмотрим применение этих символов к задачам математического анализа.
Об использовании метода инварианта, основанного на идее четности и нечетности, при решении математических задач
В этой статье рассматривается один из методов решения математических задач — метод инварианта, основанный на идеи четности и нечетности, а также специфика их при решении занимательных задач школьного курса математики.
Создание новых метрик в метрических пространствах при решении задач математического моделирования
В статье сформированы примеры функций со специальными свойствами для синтеза новых метрик в метрических пространствах.
Нелинейные вполне непрерывные операторы и их аппроксимации
В статье рассматриваем теорему о непрерывных изображениях, также рассматривается лемма о непрерывных операторах и получены к ним доказательства. Дано определение нелинейному оператору.
Нестандартные способы решения тригонометрических уравнений
В статье автор рассматривает малоизвестные и редко применяемые методы решения тригонометрических уравнений, основанные на знаниях геометрии, свойств функции, методов искусственных преобразований.
Особенности изучения тождественных преобразований в курсе алгебры основной школы
Статья анализирует важность изучения тождественных преобразований в алгебре, особенности и трудности этого процесса на различных этапах школьного обучения.
О непараметрическом оценивании взаимно неоднозначных функций по наблюдениям
Рассматривается задача восстановления функции по наблюдениям со случайными ошибками. Причем, на стадии формулировки задачи отсутствует этап, связанный с параметрической структурой этой функции, в этой связи оценка ищется в классе непараметрической ст...
Решение начальной задачи для линейных рекуррентных соотношений первого порядка в случае одношагового расщепления
Рассматривается начальная задача для неоднородного линейного рекуррентного соотношения первого порядка с операторными коэффициентами A,B, задаваемыми квадратными числовыми матрицами. Оператор A необратим, вследствие чего задача имеет решение не при к...
Условная устойчивость разностного уравнения третьего порядка в критических случаях
В статье проведено полное исследование условной устойчивости нулевого решения линейного разностного уравнения третьего порядка в критических случаях (когда значения коэффициентов уравнения находятся на границе области устойчивости). Дано полное описа...
Похожие статьи
Эффективные методы расчета спектральных задач для самосопряженных операторов
В статье обсуждается теория самосопряженных операторов. Описаны основные определения самосопряженных операторов, их связь с нормальными операторами и спектральные свойства. Кроме того, были рассмотрены классификация самосопряженных операторов и поня...
Приложения символов Ландау
Символы Ландау имеют широкий спектр приложений в области математического анализа, функционального анализа и математической физики. Ниже мы рассмотрим применение этих символов к задачам математического анализа.
Об использовании метода инварианта, основанного на идее четности и нечетности, при решении математических задач
В этой статье рассматривается один из методов решения математических задач — метод инварианта, основанный на идеи четности и нечетности, а также специфика их при решении занимательных задач школьного курса математики.
Создание новых метрик в метрических пространствах при решении задач математического моделирования
В статье сформированы примеры функций со специальными свойствами для синтеза новых метрик в метрических пространствах.
Нелинейные вполне непрерывные операторы и их аппроксимации
В статье рассматриваем теорему о непрерывных изображениях, также рассматривается лемма о непрерывных операторах и получены к ним доказательства. Дано определение нелинейному оператору.
Нестандартные способы решения тригонометрических уравнений
В статье автор рассматривает малоизвестные и редко применяемые методы решения тригонометрических уравнений, основанные на знаниях геометрии, свойств функции, методов искусственных преобразований.
Особенности изучения тождественных преобразований в курсе алгебры основной школы
Статья анализирует важность изучения тождественных преобразований в алгебре, особенности и трудности этого процесса на различных этапах школьного обучения.
О непараметрическом оценивании взаимно неоднозначных функций по наблюдениям
Рассматривается задача восстановления функции по наблюдениям со случайными ошибками. Причем, на стадии формулировки задачи отсутствует этап, связанный с параметрической структурой этой функции, в этой связи оценка ищется в классе непараметрической ст...
Решение начальной задачи для линейных рекуррентных соотношений первого порядка в случае одношагового расщепления
Рассматривается начальная задача для неоднородного линейного рекуррентного соотношения первого порядка с операторными коэффициентами A,B, задаваемыми квадратными числовыми матрицами. Оператор A необратим, вследствие чего задача имеет решение не при к...
Условная устойчивость разностного уравнения третьего порядка в критических случаях
В статье проведено полное исследование условной устойчивости нулевого решения линейного разностного уравнения третьего порядка в критических случаях (когда значения коэффициентов уравнения находятся на границе области устойчивости). Дано полное описа...











