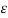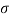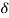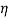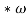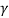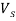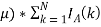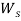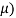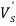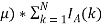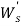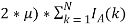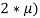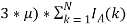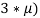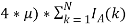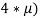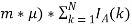Разработка математической модели финансовых рынков на основе Гауссовского случайного блуждания
Автор: Никонов Максим Викторович
Рубрика: 1. Математика
Опубликовано в
XXVII международная научная конференция «Исследования молодых ученых» (Казань, декабрь 2021)
Дата публикации: 30.11.2021
Статья просмотрена: 59 раз
Библиографическое описание:
Никонов, М. В. Разработка математической модели финансовых рынков на основе Гауссовского случайного блуждания / М. В. Никонов. — Текст : непосредственный // Исследования молодых ученых : материалы XXVII Междунар. науч. конф. (г. Казань, декабрь 2021 г.). — Казань : Молодой ученый, 2021. — С. 1-6. — URL: https://moluch.ru/conf/stud/archive/408/16785/ (дата обращения: 03.04.2025).
В статье автор пытается создать концепт новой математической модели эконометрических взаимодействий на финансовых рынках. В основу модели заложено случайное блуждание с размером шага, который варьируется в зависимости от нормального распределения. Формат торгов представлен в виде аукциона с разными показателями рынка, в основе моделирования которого лежит Гауссовское случайное блуждание. Переход состояния рынка осуществляется с помощью матрицы вероятностей перехода.
Ключевые слова: математическая модель, моделирование, финансовые рынки, вероятность.
В современном IT мире уже существуют закрытые тестирующие системы для участников фондовых рынков (дилеров, брокеров, маркетмейкеров и т. д.), созданные для решения задач скальпинга и трейдинга. Главной задачей таких систем является проверка стратегий принятия решений участниками рынка, что уменьшает некоторые операционных риски. В реализациях используются детерминированные лонгитюдные данные, то есть многомерные данные, которые получаются серией наблюдений за конкретный период времени для одних и тех же компаний. Другими словами, участники рынка тестируют алгоритмы и стратегии на одних и тех же фондовых рынках. Предлагается первичное, обобщенное тестирование на предлагаемой математической модели. Это позволит отсечь многие алгоритмы с точностью предсказания меньшей, чем методом средних арифметических и медиан рангов [1], отличающийся своей простотой и популярностью в оценке эффективности предсказаний.
В аукционе учувствуют N
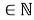
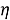
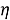
На каждом цикле участники производят на своих производствах продукцию из сырья. Сырье увеличивается на каждом цикле и представляет из себя случайный процесс:
Q
k
c
= Q
k
+ E
k
—
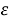
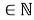
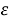
Одно производство может произвести одну единицу продукции, потратив одну единицу сырья и заплатив издержки в виде константной величины
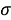
P
k
c
= P
k
+ A
k
—
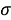
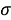
Если у участника недостаточно сырья, производств или валюты, то производство не будет удовлетворено.
На каждом цикле участник имеет возможность сделать заявку на строительство производства. Цена строительства является константной величиной
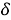
F
k
c
= F
k
+ B
k
—
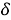
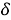
По итогам цикла с каждого участника списывается комиссия рынка
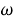
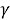
Сведем правила рынка для участников в таблице 1.
Таблица 1
Правила рынка
|
Количество |
Увеличение |
Издержки |
|
|
Сырье |
Q k |
E k |
|
|
Продукция |
P k |
A k |
|
|
Производство |
F k |
B k |
|
|
Валюта |
|
? |
Q
k
|
Каждый цикл рынок проводит аукционы по продаже и закупке выбранной продукции участников, выбирая оптимальное предложение. Единичное предложение определяется по формуле:
L
k
=
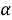
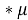
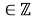
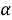
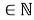
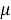
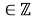
В свою очередь предложение равно:
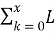
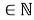
Оптимальное предложение на продажу в свою очередь определяется так:
S p = max(
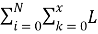
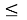
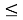
Таким образом, рынок приобретет все единицы продукции у участника с оптимальным предложением, а затем определит чье предложение будет удовлетворено следующим. Аналогично задается оптимальное предложение на покупку:
B
p
= min(
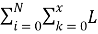
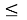
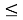
Рынок продолжит удовлетворять предложения участников до тех пор, пока количество продукции, которое закупает(продает) рынок больше нуля.
Пример. Пусть участник k
1
подал заявку на продажу
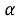
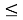
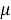
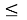
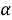
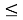
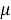
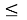
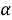
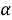
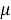
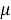
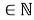
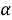
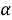
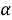
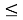
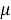
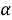
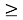
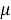
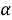
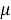
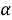
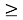
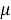
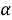
По итогам некоторого количества циклов G ≥ 0, участник, которому не хватило количества валюты на покрытие издержек, объявляется банкротом и выходит из моделирования.
Обстановка на рынке может находиться на одном из m уровней. В зависимости от уровня определяются предложения рынка на покупку и продажу продукции у участников. Определяется и цена min , цена max за единицу продукции. Значения определяются по таблице 2 уровней состояния рынка с помощью случайного блуждания [3].
Таблица 2
Уровни состояния рынка
|
Ур |
Покупка |
Продажа |
||
|
Кол - во |
цена min |
Кол-во |
цена max |
|
|
1 |
(
|
(
|
(
|
(
|
|
2 |
(
|
(
|
(
|
(
|
|
3 |
(
|
(
|
(
|
(
|
|
4 |
(
|
(
|
(
|
(
|
|
… |
… |
… |
… |
… |
|
m |
(
|
(
|
(
|
(
|
В данном случае размер шага переходов на другой уровень является обратным кумулятивным нормальным распределением
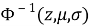
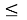
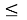
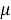
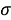
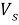
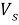
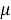
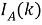
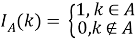
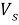
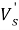
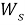
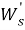
В начале моделирования уровень определяется случайным образом. Уровень для каждого следующего цикла определяется из предыдущего случайным образом в соответствии с матрицей вероятностей перехода. Отметим, что для задания матрицы перехода возможно и использование одномерного дискретного случайного блуждания — цепи Маркова [4]
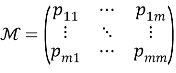
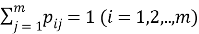
Моделирование происходит до тех пор, пока не останется единственный участник. Аукцион объявляет закрытие и начинает новое моделирование с новыми участниками.
Литература:
1. Метод средних арифметических. URL: https://clck.ru/JRFy5
2. Тасирование Фишера — Йейтса. URL: https://clck.ru/FFQy5
3. Случайное блуждание // Гауссовское случайное блуждание. URL: https://clck.ru/Z5zQJ
4. Случайное блуждание // как цепь Маркова. URL: https://clck.ru/Z5zNe
Похожие статьи
Аналитическое сравнение рекуррентных моделей в задаче прогнозирования динамики ценных бумаг
В данной статье рассматриваются подходы машинного обучения в задаче анализа и прогнозирования рынка ценных бумаг. В работе сравниваются такие аспекты, как количество занимаемой памяти, число параметров, а также величина затраченного на обучение модел...
Моделирование динамики заработной платы в Российской Федерации
В рамках модели лагов Алмон рассмотрено влияние инвестиций в основной капитал в Российской Феде-рации на уровень заработной платы. Выбиралась линейная и квадратичная структура лага. Приведены модельные соотношения и результаты их анализа в среде MATL...
Фундаментальный анализ и особенности его применения в современных условиях
На рынке существует большое количество компаний, которые являются недооцененными или переоценёнными рынком. Одним из методов поиска таких компаний является фундаментальный анализ. В данной работе рассматривается классическая схема проведения фундамен...
Оценка параметров регрессионных кривых с использованием модели Хьюбера
Для оценки параметров регрессионных кривых в подавляющем большинстве случаев используется метод наименьших квадратов, поскольку предполагается, что ошибки в данных распределены по нормальному закону. На этом же предположении строятся и доверительные ...
Моделирование логарифмически-нормальных процессов методом формирующих фильтров
При математическом моделировании сложных систем широко распространены математические модели случайных процессов, подчиняющихся логарифмически-нормальному распределению. В работе представлен машиноориентированный алгоритм генерации таких процессов, по...
Реализация новых технологий WolframAlpha в исследовании феномена «потребление»
В центре внимания статьи — практическая реализация модели Дж. Кейнса, целью которой является исследование зависимости потребления от дохода. Раскрыты прикладные возможности использования современной базы знаний и набора вычислительных алгоритмов Wolf...
Математическая модель хищник-жертва на линейном ареале
Поставлена математическая задача о двух взаимодействующих на линейном ареале популяциях по принципу хищник-жертва (модель Вольтерра). Математическая модель представляет собой краевую задачу для системы двух нелинейных дифференциальных уравнений в час...
Профилактика конфликтного поведения у подростков
Данная статья исследования состоит в предположении о том, что проведение тренинговых занятий способствует снижению уровня склонности подростков к конфликтному поведению и выбору ими оптимальных стратегий поведения в конфликтных ситуациях. Методами ис...
Математическая модель «ресурс-потребитель»
Формулируется математическая модель взаимодействия популяции и потребляемого ею трофического ресурса на отрезке, представляющая собой краевую задачу для системы двух нелинейных дифференциальных уравнений в частных производных. Исследуется на устойчив...
Аналитическая модель префиксного дерева на основе статистических свойств таблицы состояний и переходов
В работе предложена аналитическая модель структуры данных префиксного дерева, которая используется в работе алгоритма «лучевого» поиска информации. Рассматриваемая модель позволяет сократить время уплотнения разреженной таблицы состояний и переходов ...
Похожие статьи
Аналитическое сравнение рекуррентных моделей в задаче прогнозирования динамики ценных бумаг
В данной статье рассматриваются подходы машинного обучения в задаче анализа и прогнозирования рынка ценных бумаг. В работе сравниваются такие аспекты, как количество занимаемой памяти, число параметров, а также величина затраченного на обучение модел...
Моделирование динамики заработной платы в Российской Федерации
В рамках модели лагов Алмон рассмотрено влияние инвестиций в основной капитал в Российской Феде-рации на уровень заработной платы. Выбиралась линейная и квадратичная структура лага. Приведены модельные соотношения и результаты их анализа в среде MATL...
Фундаментальный анализ и особенности его применения в современных условиях
На рынке существует большое количество компаний, которые являются недооцененными или переоценёнными рынком. Одним из методов поиска таких компаний является фундаментальный анализ. В данной работе рассматривается классическая схема проведения фундамен...
Оценка параметров регрессионных кривых с использованием модели Хьюбера
Для оценки параметров регрессионных кривых в подавляющем большинстве случаев используется метод наименьших квадратов, поскольку предполагается, что ошибки в данных распределены по нормальному закону. На этом же предположении строятся и доверительные ...
Моделирование логарифмически-нормальных процессов методом формирующих фильтров
При математическом моделировании сложных систем широко распространены математические модели случайных процессов, подчиняющихся логарифмически-нормальному распределению. В работе представлен машиноориентированный алгоритм генерации таких процессов, по...
Реализация новых технологий WolframAlpha в исследовании феномена «потребление»
В центре внимания статьи — практическая реализация модели Дж. Кейнса, целью которой является исследование зависимости потребления от дохода. Раскрыты прикладные возможности использования современной базы знаний и набора вычислительных алгоритмов Wolf...
Математическая модель хищник-жертва на линейном ареале
Поставлена математическая задача о двух взаимодействующих на линейном ареале популяциях по принципу хищник-жертва (модель Вольтерра). Математическая модель представляет собой краевую задачу для системы двух нелинейных дифференциальных уравнений в час...
Профилактика конфликтного поведения у подростков
Данная статья исследования состоит в предположении о том, что проведение тренинговых занятий способствует снижению уровня склонности подростков к конфликтному поведению и выбору ими оптимальных стратегий поведения в конфликтных ситуациях. Методами ис...
Математическая модель «ресурс-потребитель»
Формулируется математическая модель взаимодействия популяции и потребляемого ею трофического ресурса на отрезке, представляющая собой краевую задачу для системы двух нелинейных дифференциальных уравнений в частных производных. Исследуется на устойчив...
Аналитическая модель префиксного дерева на основе статистических свойств таблицы состояний и переходов
В работе предложена аналитическая модель структуры данных префиксного дерева, которая используется в работе алгоритма «лучевого» поиска информации. Рассматриваемая модель позволяет сократить время уплотнения разреженной таблицы состояний и переходов ...