Реализация базового генетического алгоритма на языке высокого уровня JAVA 11



Генетический алгоритм (англ. genetic algorithm) — это эвристический алгоритм поиска, часто используемый для решения задач оптимизации и моделирования через случайный подбор, комбинирования и вариации искомых параметров с использованием механизмов, аналогичных естественному отбору в природе [1].

В рамках данной работы выполнена реализация базового генетического алгоритма на языке высокого уровня Java 11. Также проведен анализ, как производительность генетического алгоритма может варьироваться в зависимости от его параметров и конфигурации.

Перед внедрением генетического алгоритма для любого рода задач предварительно необходимо выполнить оценку, является ли генетический алгоритм правильным и подходящим для решения конкретных задач оптимизации. В качестве предварительной оценки можно воспользоваться псевдокодом:

Псевдокод для базового генетического алгоритма выглядит следующим образом:

поколение = 0; популяция [поколение] = инициализируемПоколение(размерПопуляции); оценкаПопуляции(популяция [поколение]); ПОКА условиеОкончанияВыполнено() == ложь ДЕЛАТЬ родители = выборРодителей(популяция [поколение]); популяция [поколение + 1] = скрещивание(родители); популяция [поколение + 1] = мутация(популяция [поколение + 1]); оценкаПопуляции(популяция [поколение]); поколение++; КОНЕЦ ЦИКЛА;

Псевдокод начинается с создания начальной популяции генетического алгоритма. Затем эта популяция оценивается для определения значений пригодности ее особей. Затем выполняется проверка, чтобы решить, было ли выполнено условие завершения генетического алгоритма. Если этого не произошло, генетический алгоритм начинает цикл, и популяция проходит свой первый раунд скрещивания и мутации, прежде чем, наконец, подвергнуться переоценке. Отсюда скрещивание и мутация являются непрерывными

Этот псевдокод демонстрирует базовый процесс генетического алгоритма. Далее каждый из шагов будет рассмотрен подробнее.

Нами было принято решение на разделение функциональности алгоритма на 4 класса, что позволит соблюсти базовые концепции SOLID:

1) Класс GeneticAlgorithmHelper.java: в нем имплементируем сам генетический алгоритм и опишем специфичные для конкретной задачи реализации методов интерфейса, таких как кроссовер, мутация, оценка фитнесс-функции и проверка условий завершения.

2) Отдельный класс Person.java, который представляет собой единственное решение-кандидат и его хромосому.

3) Класс Population.java, который представляет популяцию или поколение людей и применяет к ним операции на уровне группы.

4) Класс, который содержит метод “main” — BasicGA.java, некоторый загрузочный код, конкретную версию псевдокода выше и любую вспомогательную работу, которая может потребоваться для конкретной проблемы.

С целью упростить реализацию был выбран базовый бинарный генетический алгоритм [2]. Бинарные генетические алгоритмы относительно просты в реализации и могут быть невероятно эффективными инструментами для решения широкого спектра задач оптимизации. Бинарные генетические алгоритмы были первоначальной категорией генетических алгоритмов, предложенных Холландом (1975) [3].

Постановка задачи

Для реализации была выбрана задача “all-ones”, хотя она является достаточно простой, ее можно решить и с помощью бинарного генетического алгоритма. В контексте решения данной задачи рассмотрим и проанализируем фундаментальные методы для реализации алгоритма. Суть задачи заключается в поиске строки, полностью состоящей из единиц. Таким образом, для строки длиной 5 лучшим решением будет “11111”.

Параметры

После постановки проблемы, которую нужно решить, перейдем к реализации. Первое, что необходимо сделать — это сконфигурировать параметры. Как упоминалось ранее, тремя основными параметрами являются:

1) размер популяции;

2) частота мутаций;

3) частота скрещивания.

Дополнительно будем использовать принцип “элитизма” и добавим его в качестве одного из параметров алгоритма. Суть этого принципа заключается в том, что в новое поколение будут включаться лучшие родительские особи. Их число может быть от 1 и больше.

Далее в работе приводится описание класса GeneticAlgorithmHelper.java, который содержит методы и переменные, необходимые для корректной работы алгоритма. Данный класс включает в себя логику для обработки кроссовера, мутации, оценки фитнесс-функции и проверку условия завершения: ru.oshkin.GeneticAlgorithmHelper. Далее перейдем к описанию основного стартового класса, необходимого для инициализации генетического алгоритма, а также выполняющего роль “отправной” точки для программы.

Назовем этот класс “BasicGA.java” и определите метод “main”: ru.oshkin.BasicGA#main

Инициализация

Наш следующий шаг — инициализировать совокупность потенциальных решений. Обычно это делается случайным образом, но иногда может быть предпочтительнее инициализировать совокупность более систематически, возможно, для использования известной информации о пространстве поиска. В нашей работе каждый индивид в популяции будет инициализирован случайным образом. Мы можем сделать это, выбрав значение 1 или 0 для каждого гена в хромосоме случайным образом.

Перед инициализацией популяции нам нужно создать два класса: один для управления и создания популяции, а другой для управления и создания особей популяции. Именно эти классы будут содержать методы для определения пригодности индивидуума или, например, для определения наиболее приспособленного индивидуума в популяции.

Сначала мы начнем с создания отдельного класса: ru.oshkin.Person. Класс Person.java представляет собой единственное решение-кандидат и в первую очередь отвечает за хранение и управление хромосомой. Класс также имеет два конструктора. Один конструктор принимает целое число (представляющее длину хромосомы) и создает случайную хромосому при инициализации объекта. Другой конструктор принимает целочисленный массив и использует его в качестве хромосомы.

Помимо управления хромосомой индивидуума, он также отслеживает значение пригодности индивидуума, а также знает, как вывести объект на экран.

Далее создадим класс Population.java, который обеспечивает функциональность, необходимую для управления группой индивидуумов в совокупности: ru.oshkin.Population. Класс Population.java довольно прост; его основная функция заключается в хранении массива индивидуумов, к которому можно получить доступ по мере необходимости удобным способом с помощью методов класса. Такие методы, как ru.oshkin.Population#getBest и ru.oshkin.Population#setPerson, являются примерами методов, которые могут получать доступ к отдельным индивидуумам в популяции и обновлять их. В дополнение к хранению индивидуумов, он также сохраняет фитнес-функцию популяции, что можно будет использовать позже при реализации метода отбора.

Теперь, когда у нас есть классы Population.java и Person.java, мы можем использовать объекты этих классов их в классе GeneticAlgorithmHelper.java. Для этого создаем метод с именем ru.oshkin.GeneticAlgorithmHelper#initPopulation в любом месте класса GeneticAlgorithmHelper.java.

После определения популяции и написания отдельного класса возвращаемся к классу BasicGA.java и начинаем работать с методом ru.oshkin.GeneticAlgorithmHelper#initPopulation. Класс BasicGA.java имеет только метод ru.oshkin.BasicGA#main и реализует псевдокод, описанный ранее.

При инициализации популяции в основном методе нам также необходимо указать длину хромосом отдельных особей — мы будем использовать длину 40.

Оценка

На этапе оценки для каждого индивидуума в популяции вычисляется и сохраняется значение фитнесс-функции для использования в будущем. Для расчета пригодности индивида используется “фитнесс-функция”.

Генетические алгоритмы работают, выполняя отбор, чтобы направлять эволюционный процесс к формированию лучших особей. Так как именно фитнесс-функция делает возможным такой выбор, важно, чтобы она была хорошо спроектирована и обеспечивала точное значение пригодности индивидуума. Если фитнесс-функция не определена должным образом, может потребоваться больше времени, чтобы найти решение, удовлетворяющее минимальным критериям, или, возможно, вообще не удастся найти приемлемое решение.

Фитнесс-функция часто является “бутылочным горлышком” относительно всех остальных вычислительных компонентов генетического алгоритма. Поэтому важно, чтобы фитнесс-функция была оптимизирована, что поможет предотвратить появление узких мест и позволит алгоритму работать эффективно.

Каждая конкретная задача оптимизации требует уникальной разработанной фитнесс-функции. В нашем примере в задаче “all-ones” фитнесс-функция довольно проста, необходимо подсчитать количество единиц, обнаруженных в хромосоме индивидуума.

Далее добавляем метод ru.oshkin.GeneticAlgorithmHelper#calculateFitnessFunction в класс GeneticAlgorithmHelper.java. Этот метод должен подсчитывать количество единиц в хромосомах, а затем нормализовать выходные данные в диапазоне от нуля до единицы путем деления на длину хромосомы.

Нам также нужен простой вспомогательный метод для перебора каждого индивидуума в популяции и их оценки (т. е. вызова метода ru.oshkin.GeneticAlgorithmHelper#calculateFitnessFunction для каждого индивидуума). Назовем этот метод ru.oshkin.GeneticAlgorithmHelper#evaluatePopulation и опишем его также в классе GeneticAlgorithmHelper.java.

Проверка завершения

Далее необходимо проверить, было ли выполнено условие завершения. Существует много различных типов условий прекращения поиска оптимального решения. Иногда можно узнать, каково оптимальное решение (скорее, можно узнать значение пригодности оптимального решения), и в этом случае мы можем напрямую проверить правильное решение. Однако не всегда возможно определить точную пригодность наилучшего решения, поэтому мы работу алгоритма можно завершить и тогда, когда решение станет “достаточно хорошим”; то есть всякий раз, когда решение превышает некоторый порог пригодности. Мы также можем завершить работу программы досрочно, в случае если алгоритм работает долго (слишком много поколений), или мы можем объединить ряд факторов при принятии решения о завершении работы алгоритма.

Из-за простоты задачи “all-ones” и того факта, что мы знаем, что результат должен быть равен 1, в этом случае разумно завершить работу, когда будет найдено правильное решение, но так может быть не всегда. В реальности это случается крайне редко.

Далее опишем функцию ru.oshkin.GeneticAlgorithmHelper#isShouldStop, которая может проверить, выполняется ли условие завершения в классе ru.oshkin.GeneticAlgorithmHelper#isShouldStop. Описание цикла эволюции находится в основном классе программы BasicGA.java: ru.oshkin.BasicGA.

Вызов метода ru.oshkin.GeneticAlgorithmHelper#isShouldStop находится в цикле, что позволяет реализовать эволюционный цикл и проверять выходные данные. Также реализованы вызовы ru.oshkin.GeneticAlgorithmHelper#evaluatePopulation как до, так и во время цикла и определена переменная поколения (int generation), которая отслеживает номер поколения, а также используется отладочное сообщение, которое помогает узнать, как выглядит наилучшее решение в каждом поколении. При выходе из цикла мы напечатаем информацию об окончательном решении.

На этом этапе генетический алгоритм может быть запущен, но он никогда не будет эволюционировать. Мы застрянем в бесконечном цикле, если только нам не повезет настолько, что один из наших случайно сгенерированных индивидуумов окажется единственным. Это поведение можно увидеть, запустив программу на данном этапе; одно и то же решение будет представлено снова и снова, и цикл никогда не закончится. Программу потребуется завершить принудительно.

Для дальнейшей реализации генетического алгоритма, нам необходимо реализовать кроссовер и мутацию. Эти концепции фактически реализуют эволюцию популяции через случайные мутации и выживание наиболее приспособленных.

Скрещивание (кроссовер)

На этом этапе уже можно начать “развивать” популяцию, применяя мутации и скрещивания. Оператор скрещивания — это процесс, в ходе которого особи из популяции обмениваются генетической информацией, в надежде создать новую особь, которая содержит лучшие части геномов своих родителей.

Во время скрещивания каждая особь в популяции рассматривается для скрещивания; именно здесь используется параметр скорости скрещивания. Сравнивая частоту пересечений со случайным числом, мы можем решить, следует ли применять к данному индивиду пересечение или его следует сразу добавить в следующую популяцию, не затронутую пересечением. Если индивид выбран для скрещивания, то необходимо найти второго родителя. Чтобы найти второго родителя, нам нужно выбрать один из многих возможных методов отбора.

Метод рулетки

Отбор на колесе рулетки, также известный как пропорциональный отбор по пригодности — это метод отбора, который использует аналогию с колесом рулетки для отбора особей из популяции. Идея состоит в том, что отдельные люди из популяции помещаются на метафорическое колесо рулетки в зависимости от их фитнесс-функции. Чем лучше фитнесс-функция индивидуума, тем больше места ему отводится на колесе рулетки. Изображение ниже демонстрирует, как люди обычно позиционируются в этом процессе:

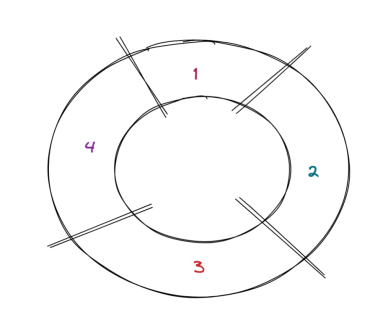
Рис. 1. Метод рулетки

Каждый цифра на колесе выше представляет отдельного человека из популяции. Чем лучше фитнесс-функция индивидуума, тем больше его доля в колесе рулетки. Если вы теперь представите, как вращаете это колесо, гораздо более вероятно, что будут выбраны более подходящие индивидуумы, потому что они занимают больше места на колесе. Вот почему этот метод отбора часто называют пропорциональным отбором пригодности; потому что решения отбираются на основе их пригодности пропорционально пригодности остальной части популяции.

Есть много других методов отбора, которые мы могли бы использовать:

1) турнирный отбор [4];

2) пропорциональный отбор [5];

3) отбор усечением [6];

4) случайный выбор [7];

5) стохастическая универсальная выборка [8].

Мы будем использовать один из наиболее распространенных методов выбора: метод рулетки.

Методы мутации

В дополнение к различным методам отбора, которые могут быть использованы во время скрещивания, существуют также различные методы обмена генетической информацией между двумя особями. Разные задачи имеют несколько разные свойства и лучше работают с конкретными методами пересечения. Например, для задачи “all-ones” просто требуется строка, полностью состоящая из единиц. Строка “00111” имеет то же значение пригодности, что и строка “10101” — они оба содержат три единицы. С генетическими алгоритмами такого типа это не всегда так. Представьте, что мы пытаемся создать строку, в которой по порядку перечислены числа от одного до пяти. В этом случае строка “12345” имеет значение пригодности, сильно отличающееся от “52431”. Это происходит потому, что мы ищем не только правильные цифры, но и правильный порядок. Для таких проблем, как эта, предпочтителен метод скрещивания, который учитывает порядок генов.

Реализуем метод равномерного скрещивания (uniform crossover). В этом методе каждый ген потомства имеет 50 %-ное изменение, исходящее либо от его первого родителя, либо от его второго родителя.

Таблица 1

Пример реализации равномерного скрещивания

Родитель 1	1	0	0	1	1
Родитель 2	0	0	1	1	0
Потомство	1	0	1	1	0

Псевдокод реализации скрещивания (кроссовера)

Определившись с методом отбора и методом мутации, определим псевдокод, который описывает процесс мутации для реализации:

ДЛЯ КАЖДОГО индивидуума В популяции: новаяПопуляция = новый массив; ЕСЛИ коэффициентМутации > рандом(): второйРодитель = выборРодителя(); потомство = мутация(индивидуум, второй родитель); новаяПопуляция.добавить(потомство); ИНАЧЕ: новоеПоколение.добавить(индивидуум); КОНЕЦ ЕСЛИ КОНЕЦ ЦИКЛА

Реализация метода скрещивания

Для реализации метода рулетки используем метод selectParent(), определенный в классе GeneticAlgorithmHelper.java:

Вызовом метода ru.oshkin.GeneticAlgorithmHelper#chooseParent запускается колесо рулетки в обратном порядке; в реальном казино на колесе уже есть разметка, а затем мы вращаем колесо и ждем, пока шарик опустится в нужное положение. Но в текущей реализации мы выбираем случайную позицию, а затем работаем в обратном направлении, чтобы выяснить, какой индивидуум находится в этой позиции. Такой подход проще для реализации. Выбираем случайное число от 0 до значения фитнесс-функции популяции, а затем повторяем цикл по каждому индивидууму, суммируя их фитнесс-функции по мере продвижения, пока не достигнем случайной позиции, которую вы выбрали в начале. Далее метод выбора родителя используется в определении метода мутации также в классе GeneticAlgorithmHelper.java.

В первой строке метода ru.oshkin.GeneticAlgorithmHelper#crossoverPopulation создается новая пустая популяция для следующего поколения. Затем совокупность зацикливается, и коэффициент кроссовера используется для рассмотрения каждого индивидуума на предмет кроссовера. Здесь также используется параметр “элитизма”, который детально будет рассмотрен далее. Если особь не проходит скрещивание, она добавляется прямо в следующую популяцию, в противном случае создается новая особь. Хромосома потомства заполняется путем перебора родительских хромосом и случайного добавления генов от каждого родителя в хромосому потомства. Когда этот процесс скрещивания завершается для каждой особи популяции, метод скрещивания возвращает популяцию следующего поколения. Метод ru.oshkin.GeneticAlgorithmHelper#crossoverPopulation реализован в классе BasicGA.java

Описанных методов достаточно для запуска и поиска решения. Одного скрещивания достаточно для развития популяции. Однако генетические алгоритмы без мутаций склонны застревать в локальных оптимумах, так и не найдя глобального оптимума. Мы не увидим, как это будет продемонстрировано в такой простой задаче, но в более сложных проблемных областях нам нужен какой-то механизм, чтобы отодвинуть популяцию от локальных оптимумов, чтобы попытаться посмотреть, есть ли лучшее решение в другом месте. Именно здесь вступает в игру случайность мутации: если решение застаивается вблизи локального оптимума, случайное событие может подтолкнуть его в правильном направлении и направить к лучшему решению.

Элитизм

Прежде чем переходить к мутации, давайте подробнее опишем параметр ru.oshkin.GeneticAlgorithmHelper#elitismCount, который мы ввели в методе скрещивания (кроссовера). Базовый генетический алгоритм часто теряет лучших особей в популяции между поколениями из-за эффектов операторов кроссовера и мутации. Однако нам нужно, чтобы эти операторы находили лучшие решения. Эту проблему можно увидеть в реальности, нужно добавить в код вывод пригодности наиболее приспособленной особи в каждом поколении. Обычно это значение повышается, но бывают случаи, когда наиболее подходящее решение теряется и заменяется менее оптимальным во время скрещивания и мутации.

Один из простых методов оптимизации, используемый для решения этой проблемы, заключается в том, чтобы всегда допускать добавление наиболее приспособленной особи или особей без изменений в популяцию следующего поколения. Таким образом, лучшие индивидуумы больше не теряются из поколения в поколение. Хотя к этим особям не применяется кроссовер, они все равно могут быть выбраны в качестве родителей для другого индивидуума, что позволяет передавать их генетическую информацию другим членам популяции. Этот процесс сохранения лучшего для следующего поколения называется элитизмом.

Как правило, оптимальное количество «элитных» особей в популяции будет составлять очень небольшую долю от общей численности популяции. Это связано с тем, что если значение слишком велико, это замедлит процесс поиска генетического алгоритма из-за отсутствия генетического разнообразия, вызванного сохранением слишком большого количества особей. Как и в случае с другими параметрами, рассмотренными ранее, важно найти баланс для оптимальной производительности.

Реализация элитизма проста как в контексте кроссовера, так и в контексте мутации. Давайте вернемся к условию в методе ru.oshkin.GeneticAlgorithmHelper#crossoverPopulation, которое проверяет, следует ли применять пересечение:

Пересечение применяется только в том случае, если соблюдены оба условия пересечения и индивидуум не считается элитным.

Что делает отдельного индивидуума элитой? На данный момент особи в популяции уже отсортированы по значению их фитнесс-функции, поэтому самые сильные особи имеют самые низкие индексы в массиве (то есть расположены в начале массива). Поэтому, если нам нужны три элитных индивидуума, мы должны исключить из рассмотрения индексы 0–3. Это сохранит самых сильных особей и позволит им перейти к следующему поколению неизменными. Мы будем использовать то же самое точное условие в последующем коде мутации.

Мутация

Последнее, что нам нужно добавить, чтобы завершить процесс эволюции — это мутация. Как и в случае с кроссовером, существует множество различных методов мутации на выбор [9]. При использовании двоичных строк один из наиболее распространенных методов называется мутацией с переворотом битов. Мутация с переворотом бита включает в себя изменение значения бита с 1 на 0 или с 0 на 1, в зависимости от его начального значения. Когда хромосома кодируется с использованием какого-либо другого представления, обычно применяется другой метод мутации, чтобы лучше использовать кодирование.

Одним из наиболее важных факторов при выборе методов мутации и скрещивания является уверенность в том, что выбранный вами метод по-прежнему дает верное решение. Мы увидим эту концепцию в действии в последующих главах, но для решения этой проблемы нам просто нужно убедиться, что 0 и 1 — единственные возможные значения, до которых ген может мутировать. Ген, мутирующий, скажем, до 7, дал бы нам неверное решение.

Этот совет кажется спорным и слишком очевидным, но рассмотрим другую простую задачу, в которой нужно упорядочить числа от одного до шести, не повторяясь (т. е. получить “123456”). Алгоритм мутации, который просто выбирает случайное число от одного до шести, может дать “126456”, используя “6” дважды, что было бы недопустимым решением, поскольку каждое число может быть использовано только один раз.

Аналогично скрещиванию (кроссовер), мутация применяется к индивидууму в зависимости от частоты мутаций. Если частота мутаций установлена равной 0.1, то каждый ген имеет 10 %-ную вероятность мутации. Функция мутации определена в классе GeneticAlgorithmHelper.java.

Метод ru.oshkin.GeneticAlgorithmHelper#mutatePopulation начинается с создания новой пустой популяции для мутировавших особей, а затем начинает перебирать текущую популяцию. Затем хромосома каждого индивидуума зацикливается, и каждый ген рассматривается на предмет мутации с переворотом бита, используя частоту мутаций. Когда вся хромосома индивидуума была зациклена, индивидуум затем добавляется к новой мутационной популяции. Когда все особи прошли через процесс мутации, мутировавшая популяция возвращается. Последний шаг цикла эволюции реализован вызовом метода ru.oshkin.GeneticAlgorithmHelper#mutatePopulation в основном цикле BasicGA.java.

На этом реализация базового генетического алгоритма завершена. Во время выполнения программа выводит информацию в консоль:

Также имеется возможность запускать программу с различными параметрами, которые определены в классе GeneticAlgorithmHelper.java:

1) ru.oshkin.GeneticAlgorithmHelper#populationSize;

2) ru.oshkin.GeneticAlgorithmHelper#mutationRate;

3) ru.oshkin.GeneticAlgorithmHelper#crossoverRate;

4) ru.oshkin.GeneticAlgorithmHelper#elitismCount.

Статистика определяет производительность генетических алгоритмов, поэтому мы не можем оценить производительность алгоритма или настроек только с помощью одного запуска — необходимо выполнить не менее 10 испытаний каждого отдельного параметра, прежде чем судить о его производительности.

Резюме

В данной работе приведен обзор базовых понятий и принципов необходимых для реализации генетического алгоритма на языках высокого уровня. Нами был использован язык Java, версия 11. Псевдокод в начале работы позволяет предоставить общую концептуальную модель для всех генетических алгоритмов: любой подвид генетического алгоритма инициализирует и выполняет оценку популяции, а затем запускает эволюционный цикл, в котором реализуется скрещивание, мутация и повторная оценка фитнесс-функции. Цикл завершается только в том случае, если выполняется условие завершения или определено условие достижения максимального числа поколений.

Необходимо отметить, что подмножество генетических алгоритмов используются для решения большого числа задач, с которыми сталкиваются в современном цифровом мире, они предназначены для решения задач оптимизации и моделирования путем последовательного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию. Внедряя генетические алгоритмы в приложения реального мира, можно решать проблемы, которые не поддаются определению традиционными вычислительными методами.

Литература:

1. Касаткина, Е. В. Разработка и тестирование генетического алгоритма для решения задачи маршрутизации / Е. В. Касаткина. — Москва: Синергия, 2021. — 448 c.
2. Карпенко, А. П. Современные алгоритмы поисковой оптимизации. Алгоритмы вдохновленные природой / А. П. Карпенко. — Москва: МГТУ им. Н. Э. Баумана, 2021. — 448 c.
3. Вирсански, Э. Генетические алгоритмы на Python / Э. Вирсански. — Москва: ДМК Пресс, 2021. — 286 c.
4. Рутковская, Д. Нейронные сети, генетические алгоритмы и нечеткие системы / Д. Рутковская, М. Пилиньский, Л. Рутковский. — Москва: Горячая Линия — Телеком, 2013. — 384 c.
5. Гладков, Леонид Генетические алгоритмы / Леонид Гладков. — Москва: Гостехиздат, 2020. — 868 c.
6. Рутковская, Д. Нейронные сети, генетические алгоритмы и нечеткие системы / Д. Рутковская, М. Пилиньский, Л. Рутковский. — Москва: Горячая Линия — Телеком, 2013. — 384 c.
7. Николенко, С. И. Глубокое обучение / С. И. Николенко, А. А. Кадурин. — Москва: Питер, 2022. — 480 c.
8. Николенко, С. И. Глубокое обучение / С. И. Николенко, А. А. Кадурин. — Москва: Питер, 2022. — 480 c.
9. Карпенко, А. П. Современные алгоритмы поисковой оптимизации. Алгоритмы вдохновленные природой / А. П. Карпенко. — Москва: МГТУ им. Н. Э. Баумана, 2021. — 448 c.
10. Ошкин, А. В. Репозиторий реализации генетического алгоритма / А. В. Ошкин. — Текст: электронный // https://github.com/: [сайт]. — URL: https://github.com/vchora96/genetic-algorithm (дата обращения: 07.06.2022).