Исследование поведения стохастической энтропии системы клеточного автомата от исходной конфигурации распределения живых клеток



Данное исследование направлено на углубленное понимание того, как начальные условия могут влиять на динамические характеристики клеточных автоматов, что может иметь значение для широкого круга приложений, включая моделирование сложных систем. Изучение динамики двумерного клеточного автомата позволяет нам глубже понять принципы самоорганизации и эмерджентного поведения в сложных системах в зависимости от параметров и начальной конфигурации живых клеток. Взаимодействие между клетками, их эволюция и формирование структур на базе простых правил предоставляют уникальную возможность исследовать процессы, которые могут быть применены для анализа реальных ситуаций, включая биологические, социальные и экономические системы. В работе показано, что начальная конфигурация распределения живых клеток существенно влияют на сценарии развития системы, а также на динамику изменения показателя стохастической энтропии. В случае начальной локализации живых клеток наблюдается экстремум энтропии, который указывает на критический момент в эволюции системы. Для случая хаотичного распределения живых клеток была зафиксирована экспоненциально убывающая зависимость показателя стохастической энтропии и последующий выход на стационарное состояние.

Ключевые слова: клеточный автомат, стохастическая энтропия, игра «Жизнь», двумерная система, время жизни, эмерджентные эффекты, дискретный набор вероятностей.

This study aims to gain a deeper understanding of how initial conditions can affect the dynamic characteristics of cellular automata, which may be important for a wide range of applications, including modeling of complex systems. Studying the dynamics of a two-dimensional cellular automaton allows us to gain a deeper understanding of the principles of self-organization and emergent behavior in complex systems depending on the parameters and initial configuration of living cells. The interactions between cells, their evolution, and the formation of structures based on simple rules provide a unique opportunity to study processes that can be applied to the analysis of real-world situations, including biological, social, and economic systems. The paper shows that the initial configuration of the distribution of living cells significantly affects the scenarios of system development, as well as the dynamics of changes in the stochastic entropy index. In the case of the initial localization of living cells, an entropy extremum is observed, which indicates a critical moment in the evolution of the system. For the case of a chaotic distribution of living cells, an exponentially decreasing dependence of the stochastic entropy index and a subsequent exit to a steady state were recorded.

Keywords: cellular automaton, stochastic entropy, game of Life, two-dimensional system, lifetime, emergent effects, discrete set of probabilities.

Введение

В истории научных исследований клеточные автоматы занимают важное место как абстрактные модели, позволяющие исследовать эмерджентное поведение и сложные системы. Одним из наиболее известных примеров клеточных автоматов является игра «Жизнь» (Life), предложенная Джоном Конвеем в 1970 году [1]. Игра «Жизнь» представляет собой исследование поведения двумерной системы на основе простых правил, смоделированных в виде клеточного автомата [2]. Концепция клеточных автоматов открывает широкие перспективы для изучения различных систем, начиная с простых моделей и заканчивая более сложными и реалистичными. Игра «Жизнь» является примером клеточного автомата, который привлекает внимание исследователей своей простотой правил и возможностью порождения разнообразных динамических структур. Анализировать динамику этой игры позволяет понять, как элементарные правила могут привести к сложному поведению системы в целом. Понимание этих процессов не только интересно с научной точки зрения, но и имеет практическое применение в различных областях, включая биологию [2], компьютерное моделирование [3], высокоскоростные генераторы псевдослучайных последовательностей [4] и кодирование информации [5,6].

Изучение динамики игры «Жизнь» также позволяет нам глубже понять принципы самоорганизации и эмерджентного поведения в сложных системах [6]. Взаимодействие между клетками, их эволюция и формирование структур на базе простых правил предоставляют уникальную возможность исследовать процессы, которые могут быть применены для анализа реальных ситуаций, включая биологические, социальные и экономические системы. Исследования в области клеточных автоматов, в том числе исследование игры «Жизнь», помогают расширить наши знания о самоорганизации, взаимодействии и возникновении сложности в природе и науке.

В данной статье мы сосредоточимся на анализе динамики игры «Жизнь», проведем исследование влияния исходной конфигурации распределения на время жизни и энтропию системы. Мы исследуем различные аспекты взаимодействия клеток, эволюцию конфигураций и вероятностные свойства таких систем. Ключевым аспектом исследования выступает показатель стохастической энтропии, или просто энтропия, которая является мерой неопределенности или случайности в системе и широко используется в областях, таких как термодинамика, теория информации и статистическая механика. В контексте двумерной системы, клеточных автоматах (Игра Жизни «Конвея»), энтропия может быть использована для анализа структуры и упорядоченности клеток [7]. Энтропия описывает, насколько непредсказуемым является исход случайного процесса, чем выше неопределенность, тем выше энтропия. В контексте двумерной системы, например, при анализе распределений состояний клеток в клеточном автомате, стохастическая энтропия позволяет оценить степень хаоса или порядка в системе [8].

Целью работы является доказательство того, что начальные условия распределения живых клеток существенно влияют на сценарии поведения развития систем, а также на динамику изменения показателя стохастической энтропии. Предполагается, что различные начальные состояния приведут к различным траекториям эволюции системы, что будет подробно проанализировано и представлено в работе. Данное исследование направлено на углубленное понимание того, как начальные условия могут влиять на динамические характеристики клеточных автоматов, что может иметь значение для широкого круга приложений, включая моделирование биологических систем, изучение сложных систем и исследование процессов самоорганизации.

Описание исследуемой системы и методов исследования

В рамках данного исследования будет рассмотрена система клеточного автомата с фиксированной размерностью сетки 100x100 и начальной концентрацией живых клеток, составляющей 0,25. Для анализа динамики и эволюции системы будут исследованы две различные конфигурации распределения живых клеток: хаотичное распределение и локализованное по центру. Объектом нашего исследования является показатель стохастической энтропии, который будет определяться для каждой из конфигураций. Мы проведем сравнительный статистический анализ двух моделей на выборке из серии экспериментов при одинаковых сценариях, чтобы выявить различия в их поведении и указать области наиболее вероятного развития исследуемых моделей.

Исходные распределения живых клеток в клеточном автомате, используемые в данной работе, представлены на рисунке 1, где можно видеть визуализацию начальных конфигураций. Дальнейший анализ будет ориентирован на выявление закономерностей в изменении стохастической энтропии для каждой из моделей, а также на оценку значимости полученных значений с использованием методов статистического анализа.

По мере эволюции клеточного автомата, мы можем отслеживать изменение энтропии на каждом шаге, что поможет анализировать, как структура и порядок системы меняются со временем. Полный пример такого подхода может быть включен в анимацию модели клеточного автомата, чтобы визуализировать динамику и отслеживать поведение систем с высоким и низким уровнем беспорядка.

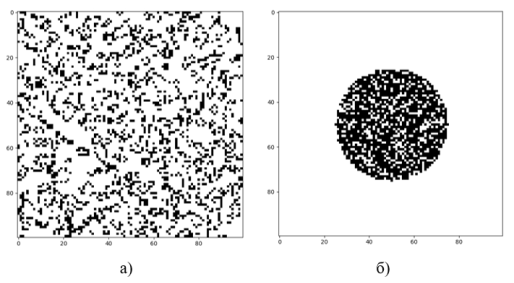
Рис. 1. Исходное распределение живых клеток по сетке клеточного автомата: А) Рандомное распределение; б) Локализация

Для расчета показателя стохастической энтропии дискретного набора вероятностей двумерной системы клеточного автомата воспользуемся формулой Шеннона [3]:

где: — энтропия случайной величины X,

— вероятность состояния n — количество возможных состояний.

Для расчета стохастической энтропии необходимо определить вероятности p _i каждого состояния. В нашем случае возможны два состояния: 0 и 1. Соответственно, нам нужно подсчитать:

– Вероятность нахождения клетки в состоянии 0 (p ₀ );

– Вероятность нахождения клетки в состоянии 1 (p ₁ );

Эти вероятности рассчитываются следующим образом:

Где — количество мертвых клеток, — количество живых клеток, N — общее количество клеток сетке клеточного автомата.

Высокая энтропия указывает на высокую степень беспорядка или случайности в сетке, в то время как низкая энтропия указывает на более упорядоченное состояние. Если все клетки мертвы или все живы, энтропия будет 0, так как нет неопределенности. В случае равного распределения живых и мертвых клеток (например, 50 % на 50 %), энтропия будет максимальной, так как случайность состояния существует на максимальном уровне.

Обсуждение результатов

В ходе данного исследования были проанализированы две различные конфигурации распределения живых клеток в модели клеточного автомата. Для каждой конфигурации был проведен ряд экспериментов, направленных на выявление областей динамики поведения системы во времени. Обе конфигурации были исследованы в одинаковых условиях: количество временных шагов было зафиксировано на уровне 1000 итераций для всех экспериментов. Это было сделано, чтобы обеспечить достаточное количество времени для выхода системы на стационарное состояние, при котором основные характеристики системы стабилизируются и перестают изменяться со временем.

На рисунке 2 представлены результаты моделирования системы клеточного автомата и тепловые карты развития для двух исследуемых типов конфигураций распределения живых клеток. Эти визуальные данные отражают различия в характере эволюции систем, обусловленные начальным распределением клеток. Анализ этих данных позволяет сделать выводы о влиянии начальных условий на динамику и конечное состояние системы. Для каждой конфигурации были построены тепловые карты, иллюстрирующие пространственно-временную эволюцию системы с динамикой активности живых клеток на исследуемом пространстве. Эти карты предоставляют наглядное представление о поведении клеточного автомата и позволяют сопоставить различные динамические сценарии в зависимости от начальных условий распределения живых клеток.

А) Исходное хаотичное распределение

Б) Исходная локализация

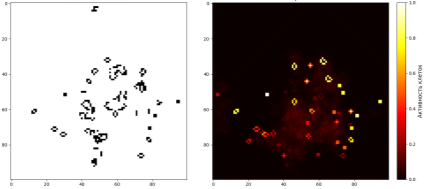
Рис. 2. Результаты моделирования системы клеточного автомата и тепловые карты развития для двух исследуемых типов конфигураций распределения живых клеток

В результате проведенной серии численных экспериментов для каждого типа начальных распределений живых клеток были построены графики, характеризующие динамику изменения количества живых клеток и поведения стохастической энтропии во времени (рисунки 3 и 4). Данные графики предоставляют подробное понимание процесса эволюции системы клеточного автомата при различных начальных условиях. На графиках также указаны области вероятного отклонения в 5 % и 10 %, что позволяет наглядно представить диапазон возможных флуктуаций в поведении численных экспериментов. Эти области вероятного отклонения важны для понимания степени разброса данных и оценки надежности полученных результатов.

а)

б)

Рис. 3. Динамика количества живых клеток от времени с указанными областями вероятного поведения: а — хаотичное распределение, б — исходная локализация живых клеток

а)

б)

Рис. 4. Динамика показателя стохастической энтропии для исследуемых систем: а — хаотичное распределение, б — локализация живых клеток

Анализ численных данных позволил выявить закономерности и определить соответствующие уравнения регрессии, которые будут использованы для дальнейшего статистического анализа исследуемых систем. Эти уравнения регрессии предоставляют математическую основу для статистического анализа модели клеточного автомата для описания изменений в таких параметрах, как количество живых клеток и стохастическая энтропия, с течением времени.

Проведенный анализ выявил значимые различия в поведении систем в зависимости от начальных условий распределения живых клеток. Например, системы с хаотичным распределением демонстрируют более сложные траектории изменения количества живых клеток и стохастической энтропии по сравнению с системами, где начальные распределения локализованы по центру. Эти различия были количественно оценены и подробно представлены в модели регрессионного анализа в Таблице 1.

Таблица 1

Статистический анализ исследуемых моделей клеточного автомата с различием по конфигурациям распределения

Исходное распределение	Время выхода на стационарное состояние	Дисперсия модели		Среднеквадратическое отклонение в данных
		Энтропия	Количество живых клеток	Энтропия	Количество живых клеток
Хаотичное	648 15	0,00918	10196	0,0958	100,798
Локализация	732 13	0,00602	1719,92	0,0775	41,47

В ходе проведенных численных экспериментов удалось выявить значительные различия в динамике изменения показателя энтропии для систем с различными исходными распределениями живых клеток. В случае начальной локализации живых клеток наблюдается экстремум энтропии, соответствующий моменту перехода от фазы роста к фазе убыли количества живых клеток. Этот экстремум указывает на критический момент в эволюции системы, когда структура распределения живых клеток достигает наивысшей сложности, после чего начинается процесс упорядочивания и снижения энтропии. Для случая хаотичного распределения живых клеток была зафиксирована явно экспоненциально убывающая зависимость показателя стохастической энтропии. Это свидетельствует о резком переходе системы к процессу убыли количества живых клеток и последующему выходу на стационарное состояние. В данном сценарии система быстро упрощается и стабилизируется, что отличает её поведение от случая с локализованным начальным распределением.

Анализ большого количества экспериментальных данных позволил выделить области вероятных колебаний соответствующих зависимостей поведения энтропии. Эти области дают представление о возможных вариациях в динамике систем, позволяя оценить степень вариабельности и надежности наблюдаемых закономерностей. Кроме того, подробное исследование показало, что причиной различий в динамике энтропии является неоднородность начальных условий, которая определяет характер взаимодействий между живыми клетками в процессе эволюции. Локализованные начальные условия способствуют более сложной динамике с появлением промежуточных состояний, тогда как хаотичное распределение ведет к быстрому упрощению и стабилизации системы.

В заключение, исследование продемонстрировало значимость начальных условий в модели клеточного автомата для различных типов распределения живых клеток. Полученные результаты могут быть полезны для дальнейшего изучения сложных систем и моделирования процессов самоорганизации в различных прикладных областях, включая биологические системы, физические модели и теорию информации.

Заключение

Доказано, что начальная конфигурация распределения живых клеток существенно влияют на сценарии эволюции системы, а также на динамику изменения показателя стохастической энтропии. В случае начальной локализации живых клеток наблюдается экстремум энтропии, соответствующий моменту перехода от фазы роста к фазе убыли количества живых клеток. Этот экстремум указывает на критический момент в эволюции системы, когда структура распределения живых клеток достигает наивысшей сложности, после чего начинается процесс упорядочивания и снижения энтропии. Для случая хаотичного распределения живых клеток была зафиксирована явно экспоненциально убывающая зависимость показателя стохастической энтропии. Это свидетельствует о резком переходе системы к процессу убыли количества живых клеток и последующему выходу на стационарное состояние.

Литература:

1. Wolfram S., Gad-el-Hak M. A new kind of science //Appl. Mech. Rev. — 2003. — Т. 56. — №. 2. — С. B18-B19.
2. Peña E., Sayama H. Life worth mentioning: complexity in life-like cellular automata //Artificial Life. — 2021. — Т. 27. — №. 2. — С. 105–112.
3. Wuensche A. Cellular automata encryption: the reverse algorithm, Z-parameter and chain-rules //Parallel Processing Letters. — 2009. — Т. 19. — №. 02. — С. 283–297.
4. Сухинин Б. М. Высокоскоростные генераторы псевдослучайных последовательностей на основе клеточных автоматов //Прикладная дискретная математика. — 2010. — №. 2 (8). — С. 34–41.
5. Евсютин О. О., Шелупанов А. А. Основные подходы к использованию математического аппарата теории клеточных автоматов для решения задач кодирования информации //Доклады Томского государственного университета систем управления и радиоэлектроники. — 2014. — №. 2 (32). — С. 60–65.
6. Евсютин О. О., Шелупанов А. А. Приложения клеточных автоматов в области информационной безопасности и обработки данных //Доклады Томского государственного университета систем управления и радиоэлектроники. — 2012. — №. 1–2 (25). — С. 119–125.
7. Нормантас В. Использование компрессии данных для оценки энтропии простейших клеточных автоматов //Новые информационные технологии в автоматизированных системах. — 2015. — №. 18. — С. 265–269.
8. Малинецкий Г. Г., Щадинский Д. М. Конструирование вычислительного устройства на основе игры «Жизнь» //Препринты Института прикладной математики им. МВ Келдыша РАН. — 2019. — №. 0. — С. 143–14.