Математическое моделирование процесса работы ротационного культиватора
Авторы: Захаров Павел Владимирович, Лысыч Михаил Николаевич, Шабанов Михаил Леонидович
Рубрика: 14. Общие вопросы технических наук
Опубликовано в
Дата публикации: 16.09.2014
Статья просмотрена: 284 раза
Библиографическое описание:
Захаров, П. В. Математическое моделирование процесса работы ротационного культиватора / П. В. Захаров, М. Н. Лысыч, М. Л. Шабанов. — Текст : непосредственный // Современные тенденции технических наук : материалы III Междунар. науч. конф. (г. Казань, октябрь 2014 г.). — Казань : Бук, 2014. — С. 77-81. — URL: https://moluch.ru/conf/tech/archive/123/6143/ (дата обращения: 03.04.2025).
При большом разнообразии машин для рыхления почвы и уничтожения сорняков в рядах и междурядьях лесных полос все они имеют ряд недостатков, снижающих качество ухода. В частности, орудия уплотняют почву ниже глубины обработки, сдвигают и засыпают часть лесных культур почвой, оставляют холмики, в которых почва недостаточно разрыхлена (не уничтожаются многолетние сорняки) [1]. С целью устранения перечисленных недостатков разработана конструкция ротационного рабочего органа (рис. 1, а), выполненный в виде установленной на наклонной оси свободно вращающейся звездочки с радиально расположенными пальцами.
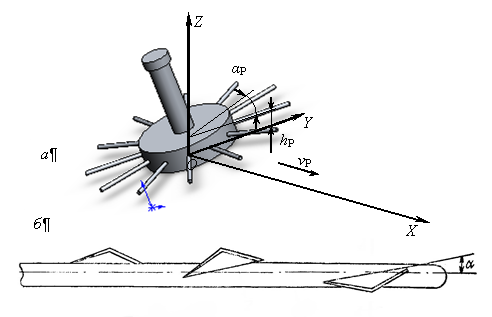
Рис. 1. Расположение системы координат по отношению к моделируемому механизму (а) и схема расположения рыхлящих элементов ротационного рабочего органа культиватора-рыхлителя (б)
В предложенном ротационном рабочем органе, для увеличения интенсивности рыхления почвы и улучшения самоочищения ротационных рабочих органов, на наклонной оси расположена коническая шестерня, входящая в зацепление с шестернями, установленными на внутренних концах радиальных пальцев (рис.1, б). На пальцах по винтовой линии расположены рыхлящие элементы, которые установлены с определенным смещением друг относительно друга [2].
Для теоретической проверки работоспособности разработанной конструкции и оптимизации параметров ротационного рабочего органа была разработана математическая модель, базирующаяся на методах классической динамики. Анализ механизма позволил составить систему дифференциальных уравнений, описывающую эволюцию механизма с течением времени под воздействием внешних воздействий: вращающего момента со стороны вала отбора мощности и сил сопротивления со стороны обрабатываемой почвы [3]. Система координат XYZ для описания механизма вводится так, чтобы поступательное движение осуществлялось вдоль оси OX (рис. 1, а), центр ротора находился на высоте hР над уровнем почвы (плоскостью XOY), а плоскость, в которой лежат пальцы ротора, была наклонена под углом αР к оси OY.
Ротационный рабочий орган представляется в модели состоящим из отдельных абсолютно твердых тел, взаимодействующих между собой в некоторых заданных точках. В модели необходимо учитывать движение следующих тел: ведущего вала, ведущей шестерни, корпуса рабочего органа, восьми (или другого количества) пальцев. Остановимся подробно на описании движения каждого из элементов механизма.
Вал механизма в рамках модели вращается с постоянной угловой скоростью:
ωВ = const. (1)
При этом угловое положение вала φВ в любой момент времени t можно рассчитать по формуле:
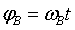 . (2)
. (2)
Шестерня совершает вращательное движение относительно оси вала механизма, при этом с валом осуществляется вязкоупругое вращательное взаимодействие MВШ (рис. 2, а). Кроме того, на шестерню действуют момент сил сухого трения в подшипнике MШТр (который может зависеть от некомпенсированных сил со стороны пальцев) и моменты сил FШПi в точках соприкосновения с ведомыми шестернями на пальцах.
В этом случае основное уравнение динамики вращательного движения записывается следующим образом:
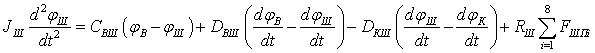 , (3)
, (3)
где JШ — момент инерции шестерни относительно оси; φВ, φШ и φК — текущие углы поворота вала, шестерни и корпуса; СВШ и DВШ — жесткость и коэффициент демпфирования вязкоупругого углового взаимодействия вала и шестерни; DКШ — коэффициент вязкого трения между шестерней и корпусом; RШ — радиус шестерни (расстояние от оси до точки контакта ведущей и ведомой шестерен); FШПi — касательная составляющая силы, действующей со стороны ведомой шестерни i на ведущую.
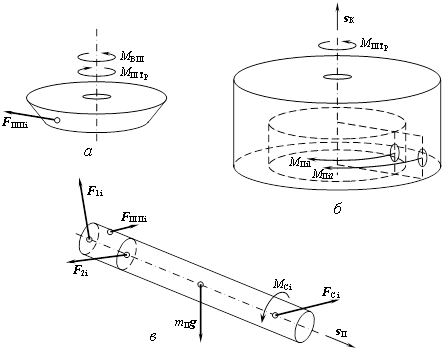
Рис. 2. Расчетные схемы к составлению уравнений движения шестерни (а), корпуса (б) и пальца (в)
При этом считаем, что момент трения между корпусом и валом зависит линейно от разности скоростей вращения корпуса и вала, но не зависит от изгибающих сил, возникающих в подшипнике.
В рамках модели считается, что корпус ротационного рабочего органа совершает только вращательное движение относительно оси механизма. На его вращение оказывают влияние моменты MПi1 и MПi2 сил, возникающих в подшипниках закрепления пальцев (рис. 2, б). Также в основном уравнении динамики вращательного движения необходимо учесть момент сил вязкого трения между корпусом и валом:
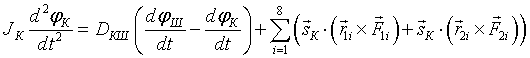 , (4)
, (4)
где JК — момент инерции корпуса относительно оси; sК — вектор направления оси корпуса;
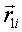 и
и 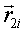 — радиус-векторы от центра корпуса до центров первого и второго подшипника крепления пальца i;
— радиус-векторы от центра корпуса до центров первого и второго подшипника крепления пальца i;
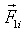 и
и 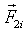 — силы в первом и втором подшипниках крепления пальца i.
— силы в первом и втором подшипниках крепления пальца i.
Каждый палец в процессе работы механизма совершает сложное движение — как вращательное, так и поступательное, и испытывает действие большого количества сил: в подшипниках закрепления, силы тяжести, сил со стороны разрыхляемой почвы (рис. 2, в). Уравнения движения пальца i записываются следующим образом:
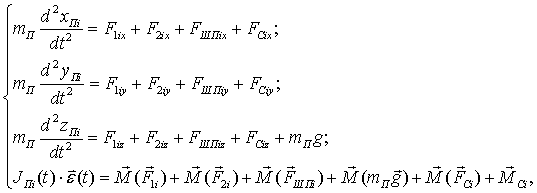 (5)
(5)
где mП — масса пальца; F1ix, F1iy, F1iz — декартовы составляющие силы в первом подшипнике; F2ix, F2iy, F2iz — декартовы составляющие силы во втором подшипнике; FШПix, FШПiy, FШПiz — декартовы составляющие силы взаимодействия с ведомой шестерней; FСix, FСiy, FСiz и MCi — декартовы составляющие силы и момент сопротивления со стороны почвы; mПg — сила тяжести.
При работе ротационного механизма каждый палец вращается как вокруг своей геометрической оси, так и вместе с корпусом вокруг оси вала. При этом получается, что в каждый момент времени t ось «мгновенного» вращения пальца не совпадает ни с геометрической осью пальца, ни с осью вала. Вследствие этого при расчете необходимо вычислять зависимость момента инерции пальца JП от направления мгновенной оси вращения для любого t. Так как палец имеет сложную конструкцию (цилиндрический стержень, ведомая шестерня, рыхлящие элементы) аналитический расчет момента инерции затруднен, и расчет момента инерции ведется на основе метода конечных элементов. Объем пальца разбивается на большое количество N элементарных кубов с учетом сложной формы пальца, затем момент инерции рассчитывается по формуле
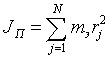 , (6)
, (6)
где mэ — масса элементарного куба; rj — расстояние от центра элементарного куба до оси вращения.
Каждый палец вращается в двух подшипниках, которые в свою очередь установлены в корпусе. Каждый подшипник в модели заменяется парой точек: одна точка на корпусе, другая на пальце. Обозначим точки на корпусе как K1i и K2i, а точки на i-пальце P1i и P2i. При смещении точки Pj относительно соответствующей точки Kj в подшипниках возникают силы, стремящиеся снова совместить точки Pj и Kj. Так как по природе это силы упругого взаимодействия стальных элементов подшипников, возникающие силы в модели учитываются следующим образом:
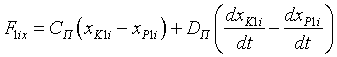 ;
;
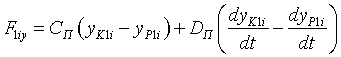 ; (7)
; (7)
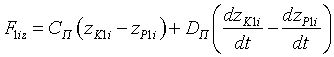 ,
,
где CП и DП — коэффициент упругости и коэффициент демпфирования; xK1i, yK1i, zK1i — координаты точки K1i; xP1i, yP1i, zP1i — координаты точки P1i.
Аналогичным образом вычисляются силы, возникающие в подшипнике 2 на i-м пальце.
При вращении корпуса координаты точек K1i и K2i постоянно изменяются. В модели координаты указанных точек, соответствующие текущему значению угла поворота корпуса φК рассчитываются следующим образом.
Во-первых, точки-подшипники распределяются равномерно по окружности корпуса:
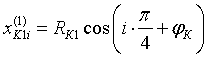 ;
; 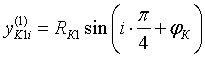 ;
; 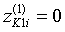 ; (8)
; (8)
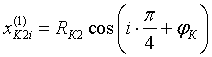 ;
; 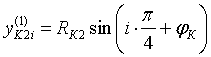 ;
; 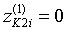 , (9)
, (9)
где i — индекс подшипника.
Во-вторых, необходимо учесть, что ротор установлен под углом αР к поверхности почвы. Для этого координаты пересчитываются следующим образом:
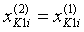 ;
; 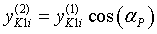 ;
; 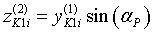 ; (10)
; (10)
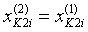 ;
; 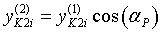 ;
; 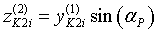 . (11)
. (11)
И, наконец, производится перемещение рабочего органа в горизонтальном направлении на расстояние vРt и в вертикальном — на расстояние hР:
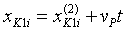 ;
; 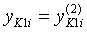 ;
; 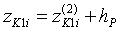 ; (12)
; (12)
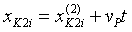 ;
; 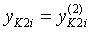 ;
; 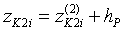 . (13)
. (13)
Координаты точек P1i и P2i зависят от положения и угла поворота пальца и в процессе численного интегрирования подлежат постоянному пересчету.
Силы в точке взаимодействия ведущей и ведомой шестерни рассчитываются следующим образом. Угловая скорость ведомой шестерни пропорциональна разности угловых скоростей ведомой шестерни и корпуса:
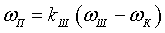 , (14)
, (14)
где kШ — передаточное отношение.
При отсутствии контакта пальцев с почвой корпус механизма старается раскрутиться так, чтобы корпус начал вращаться с одинаковой скоростью с ведущей шестерней. В этом случае потери на трение в подшипниках пальцев минимальны. В случае же торможения пальцев почвой скорость вращения корпуса становится меньше скорости вращения ведущей шестерни, и за счет разности скоростей ωШ и ωК раскручиваются пальцы.
В формуле для силы, возникающей в точке контакта ведущей и ведомой шестерен, необходимо учесть, что силы появляются вследствие несоответствия углов ведущей и ведомой шестерен:
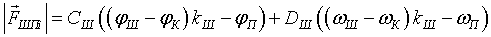 , (15)
, (15)
где CШ и DШ — коэффициенты упругости и демпфирования углового упругого взаимодействия шестерен; φП — угол поворота пальца относительно его оси; ωП — угловая скорость пальца, приведенная к его оси.
Так как возникающая сила FШПi перпендикулярна оси пальца и оси корпуса, направление силы вычисляется через векторное произведение направляющих векторов 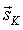 и
и 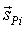 :
:
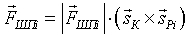 . (16)
. (16)
Рассчитанная таким образом сила 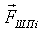 подставляется далее в уравнения движения шестерни (3) и пальца (5).
подставляется далее в уравнения движения шестерни (3) и пальца (5).
При моделировании взаимодействия рабочих органов с почвой последняя считается вязкой средой [4]. В первом приближении силу со стороны почвы можно рассчитать, учитывая скорость движения конца пальца и степень его заглубления в почву.
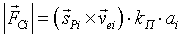 , (17)
, (17)
где 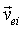 — скорость конца пальца; kП — коэффициент линейной вязкости почвы; ai — доля длины пальца, находящаяся в почве.
— скорость конца пальца; kП — коэффициент линейной вязкости почвы; ai — доля длины пальца, находящаяся в почве.
Подводя итог аналитическим выкладкам, отметим, что механизм в целом описывается системой дифференциальных уравнений (1–5), при этом переменные, входящие в систему, рассчитываются по формулам (6–17). Из-за громоздкости системы поиск ее аналитического решения затруднен, однако численное решение системы может быть найдено. Решение системы уравнений производили усовершенствованным методом Эйлера-Коши [5]. Шаг численного интегрирования Δt определяли путем многократного проведения экспериментов с последовательно уменьшающимся в два раза шагом и остановились на шаге, после которого результаты моделирования практически не изменяются (изменение составляет не более 1–2 %). Определенный таким образом шаг составил Δt = 2,0·10–4 с.
Для решения системы дифференциальных уравнений, положенной в основу модели, и удобства проведения различных компьютерных экспериментов с моделью составлена компьютерная программа «Программа для моделирования ротационного рабочего органа культиватора-рыхлителя» на языке Object Pascal в интегрированной среде программирования Borland Delphi 7.0 [6].
Программа позволяет задавать значения 20 основных конструктивных и технологических параметров культиватора [6].
Таким образом, разработана математическая модель ротационного рабочего органа на основе методов классической динамики, позволяющая на основе компьютерных экспериментов исследовать влияние на эффективность функционирования ротационного культиватора конструктивных параметров, параметров взаимодействия с почвой, технологических параметров. Модель позволила убедиться в работоспособности предложенной конструкции ротационного культиватора-рыхлителя и позволит в дальнейшем провести теоретическую оптимизацию его параметров.
Литература:
1. Бартенев, И. М. Борьба с сорной растительностью в защитных лесных насаждениях [Текст] / И. М. Бартенев. — М.: Колос, 1991. — 47 с.
2. А. с. 380256 СССР, МКИ A 01 В 35/16, A 01 В 39/16. Ротационный рабочий орган культиватора-рыхлителя [Текст] / И. М. Бартенев [и др.]; И. М. Бартенев, В. В. Попов, Ю. М. Жданов, В. Л. Аравийский; заявитель и патентообладатель: ВНИАЛМИ. — № 1702643; заявл. 04.10.1971; опубл. 15.05.73, Бюл. № 21. — 2 с.
3. Расчет и проектирование строительных и дорожных машин на ЭВМ [Текст] / Под ред. Е. Ю. Малиновского. — М.: Машиностроение, 1980. — 216 с.
4. Моделирование сельскохозяйственных агрегатов и их систем управления: [учеб. для вузов] [Текст] / под ред. А. Б. Лурье. — Л.: Колос, 1979. — 312 с.
5. Инженерные расчеты на ЭВМ: [Справочное пособие] [Текст] / Под ред. В. А. Троицкого. — Л.: Машиностроение, 1979. — 288 с.
6. Свидетельство о государственной регистрации программы для ЭВМ № 2009613046 «Программа для моделирования ротационного рабочего органа культиватора-рыхлителя».











