Трехмерная визуализация результатов томографического контроля

Введение

В медицинском обследовании и промышленной диагностике в настоящее время не известно более информативного метода исследования внутренней структуры, чем компьютерная томография (КТ). Независимо от вида проникающего излучения (ультразвук, рентгеновское и гамма-излучение, магнитные поля и пр.) результатом КТ является набор плоских сечений объекта исследования — серия томограмм. Хотя одна томограмма несет в себе достаточную информацию о внутренней структуре объекта в плоскости сечения — координаты, размеры внутренних элементов (органов) — она не позволяет определить их точную форму и протяженность в пространстве. В качестве примера рассмотрим куб, произвольно ориентированный в пространстве, и его сечения плоскостью Z = 0. При положении куба, параллельном секущей плоскости, сечение принимает форму квадрата (рис. 1, а), а при других положениях — треугольника (рис. 1, б), трапеции (рис. 1, в) и многоугольника (рис. 1, г).

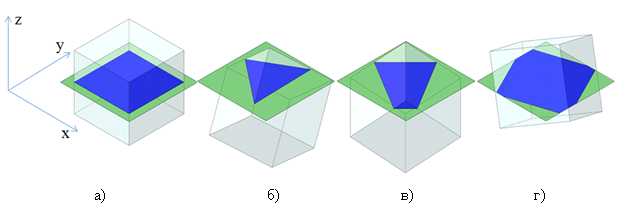Рис. 1. Сечения куба при различных его положениях в пространстве

Таким образом, один и тот же объект контроля, при различном положении в пространстве, дает различные изображения сечений, и возникают трудности при идентификации полученных изображений. Объемное представление объекта гораздо информативнее набора плоских сечений, поэтому особо актуальной является задача трехмерного отображения полученного объема.

Анализ существующих средств трехмерной визуализации

На данный момент существует большое количество программных продуктов для построения трехмерного изображения объекта по его плоским сечениям, как коммерческих (Avizo, Amira, VGStudio MAX), так и с открытым доступом (ImageVis3D, Voreen, VolView, 3D Slicer). Кроме того, существует огромное число методов объемного представления (рендеринга), которые могут быть использованы для разработки собственного средства визуализации. Объемная модель может быть получена прямым объемным рендерингом или косвенными методами — путем построения полигональной сетки на основе входных данных [1], проекционными методами [2, 3].

Наибольший интерес представляют методы прямого рендеринга, при котором каждому элементу объема приписывается определенная яркость, цвет и прозрачность при помощи передаточной функции, что позволяет одновременно выделить из исходного набора данных множество структур, имеющих различную плотность. Передаточная функция может задаваться кусочно-линейной функцией или таблицей значений.

Прямой рендеринг является сложной вычислительной задачей, которую можно выполнить двумя способами:

-        рендеринг прямого хода (back-to-front), к которому относятся методы множественных преобразований [4, 5], метод сплэттинга (splatting) [6, 7], сдвиговые алгоритмы (например, сдвиговая деформация (shear-warp) [8]), текстурный рендеринг (texture-based volume rendering) [9];

-        рендеринг обратного хода (front-to-back), к которому относятся методы трассировки (ray tracing) [10, 11] и отслеживания (ray casting) [11] лучей.

Разработка средства визуализации

На основе проведенного анализа существующих решений в области построения трехмерного объема основой разработки программы визуализации выбран метод текстурного рендеринга [9]. Этот метод основан на формировании объема путем наложения сечений друг на друга. В процессе наложения каждое сечение подвергается операции смешивания (blending) для комбинирования цвета выводимого пикселя с пикселем, который уже находится на экране. Кроме того, отбрасываются «черные» пиксели, которые представляют собой отсутствие объекта.

В среде программирования C++ Builder 6 c использованием библиотеки GLUT (OpenGL Utility Toolkit), входящей в состав API OpenGL, разработана программа трехмерной визуализации, входными данными для которой служит набор плоских сечений. Объем (до 512³) формируется путем генерации 2D текстур в каждой плоскости системы координат. Таким образом, имея в каждой плоскости набор изображений, возможно построение сечения объекта на основании данных изображений.

Рассмотрим процесс создания и наложения текстур в плоскости X = 0. В первую очередь выделяется память размером xsiz для хранения текстуры texturesX и создается текстура, которая будет сохранена в этой памяти: glGenTextures(xsiz, texturesX).

Затем указывается тип текстуры: glBindTexture(GL_TEXTURE_2D, texturesX [x]), в данном случае texturesX [] — это двумерная текстура (GL_TEXTURE_2D).

Включается режим наложения текстур: glEnable(GL_TEXTURE_2D).

Задается тип фильтрации для увеличенного и уменьшенного изображения:

glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR).

Создается фактическая 2D текстура: glTexImage2D(GL_TEXTURE_2D, 0, GL_INTENSITY, ysiz, zsiz, 0, GL_LUMINANCE, GL_UNSIGNED_BYTE, slice),

где ysiz, zsiz — ширина и высота текстуры; slice — указатель на данные в texturesX.

Изображение трехмерного объекта обычно представляется в виде куба, на грани которого накладываются изображение, поэтому необходимо определить какая текстура будет накладываться на каждую грань. Это выполняется с помощью команды:

glBindTexture(GL_TEXTURE_2D, texturesX [slice]),

где slice — номер текстуры из набора текстур texturesX [], используемой для наложения.

Команда glBindTexture() также позволяет строить сечения объекта, изменяя значение параметра slice.

После того, как выбрана нужная текстура, необходимо наложить ее на соответствующую грань куба, для этого используются команды glTexCoord2f() и glVertex3f() [12] для всех вершин грани.

Для реализации смешивания используется набор команд, включающих режим смешивания glEnable() и определяющих glBlendFunc(), как будет реализовано данное смешивание:

glEnable(GL_BLEND);

glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA).

Для плоскостей Y = 0 и Z = 0 выполняются аналогичные операции. Результаты работы разработанной консольной программы представлены на рис. 2.

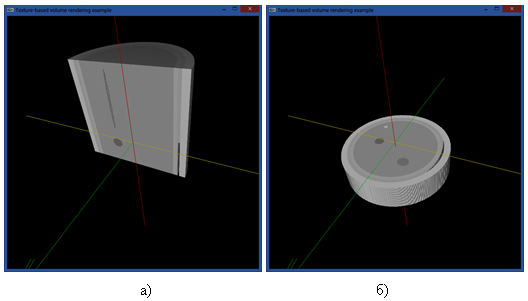
Рис. 2. Результаты визуализации объекта: а — сечение плоскостью Y = 0; б — сечение плоскостью Z = 0

В результате проведенной работы разработан гибкий инструмент трехмерной визуализации, позволяющий:

-        производить построение 3D модели на основе набора плоских сечений;

-        осуществлять вращение и масштабирование отображаемого объекта;

-        строить сечения объекта тремя плоскостями;

-        отбрасывать неинформативные данные, не принадлежащие объекту.

Литература:

1.      Marching Cubes: A High Resolution 3D Surface Construction Algorithm / William E. Lorensen, Harvey E.Cline — Computer Graphics (SIGGRAPH 87 Proceedings). Vol. 21, N. 4, 1987, pp. 163–169.

2.      Wallis J. W., Miller T. R. Three-dimensional display in nuclear medicine and radiology. J. Nucl. Med. Vol. 32 (3), 1991, pp. 532–546.

3.      Sato Y., Shiraga N., Nakajima S., Tamura S., Kikinis R.: Local Maximum Intensity Projection (LMIP): A New Rendering Method for Vascular Visualization // Journal of Computer Assisted Tomography. Vol. 22, N. 6, 1998, pp. 912–917.

4.      Vezina G., Fletcher P., Robertson P. K. Volume Rendering on the MasPar MP-1 // Proc. of 1992 Workshop on Volume Visualization. Boston, MA, 1992, pp. 3–8.

5.      Schroeder P., Salem J. B. Fast Rotation of Volume Data on Data Parallel Architecture // Proc. of Visualization'91, San Diego, 1991. P. 50.

6.      Westover L. A. Splatting: A Parallel, Feed-Forward Volume Rendering Algorithm: PhD thesis: The University of North Carolina at Chapel Hill, Department of Computer Science, July 1991.

7.      Huang J., Mueller K., Shareef N., Crawfis R. FastSplats: Optimized Splatting on Rectilinear Grid // Proc. of IEEE Visualization Conference. 2000, pp. 219–226.

8.      Lacroute P., Levoy M. Fast Volume Rendering Using a Shear-Warp Factorization of the Viewing Transformation // Proc. SIGGRAPH '94. 1994, pp. 451–458.

9.      Hibbard W., Santek D. Interactivity is the key // Chapel Hill Workshop on Volume Visualization, University of North Carolina, Chapel Hill, 1989, pp. 39–43.

10.  Levoy M. Efficient ray tracing of volume data // ACM Trans. on Graphics. Vol. 9 (3), 1990, pp. 245–261.

11.  Weiskopf D. GPU-Based Interactive Visualization Techniques // Springer Science & Business Media. 2006, p. 21.

12.  Баяковский Ю. М., Игнатенко А. В. и др. Графическая библиотека OpenGL // Учебно-методическое пособие. — М.: Изд-во ВМиК МГУ, 2003. — 132 с.