Математические модели и методы обработки информации в системах испытания электрооборудования на надежность
Авторы: Русин Александр Юрьевич, Абдулхамед Мохаммед Абдулкарим Номан
Рубрика: 3. Автоматика и вычислительная техника
Опубликовано в
IV международная научная конференция «Технические науки в России и за рубежом» (Москва, январь 2015)
Дата публикации: 18.12.2014
Статья просмотрена: 256 раз
Библиографическое описание:
Русин, А. Ю. Математические модели и методы обработки информации в системах испытания электрооборудования на надежность / А. Ю. Русин, Мохаммед Абдулкарим Номан Абдулхамед. — Текст : непосредственный // Технические науки в России и за рубежом : материалы IV Междунар. науч. конф. (г. Москва, январь 2015 г.). — Москва : Буки-Веди, 2015. — С. 36-42. — URL: https://moluch.ru/conf/tech/archive/124/6943/ (дата обращения: 23.04.2025).
Надежность технических изделий, из-за применения новых более прочных материалов, новых конструктивных решений, возрастает. Если не совершенствовать модели ускоренных испытаний оборудования на надежность, то время проведения испытаний возрастет и неизбежно приведет увеличению затрат на них.
Существует несколько разработанных планов испытаний. Рассмотрим план [N,U,T], который приведен в стандарте [1]. Согласно этому плану, одновременно испытывают N объектов, отказавшие во время испытаний объекты не восстанавливают и не заменяют, испытания прекращают по окончании времени окончания или достижения наработки Т для каждого не отказавшего объекта. В более новом стандарте [2], действующем в настоящее время, также существует план испытаний, подобный этому. Он называется планом, ограниченным продолжительностью наблюдений.
При проведении испытаний по плану [N,U,T] образуются однократно цензурированные выборки наработок на отказ. При параметрическом оценивании показателей надежности, например, средней наработки до отказа, по однократно цензурированным справа выборкам основным математическим методом является метод максимального правдоподобия. В условиях постоянного повышения надежности испытываемого оборудования и желаемого сокращения времени испытаний, становится актуальным вопрос исследования достоверности оценок максимального правдоподобия (МП).
В работе выполнены экспериментальные исследования точности оценок МП экспоненциального закона распределения по малым, однократно цензурированным справа выборкам, формирующимся по плану [N,U,T].
На ЭВМ моделировались однократно цензурированные справа выборки случайных величин объемом N=5, 10, 15, 20, 25. Генерирование выборок выполнялось при следующих ограничениях
6 £ N < 10, q ³ 0,5
10 £ N < 20, q ³ 0,3
20 £ N £ 50, q ³ 0,2,
где q — степень цензурирования выборки. Ограничения приняты в соответствии с рекомендациями [7].
Количество сформированных выборок для каждого значения N равно 3000. По каждой выборке методом максимального правдоподобия рассчитывались оценки экспоненциального распределения и их относительные отклонения d от истинных значений — значений, которые использовались при генерации выборки.
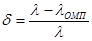 , (1)
, (1)
где 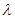 — истинное значение параметра экспоненциального распределения,
— истинное значение параметра экспоненциального распределения,
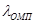 — оценка максимального правдоподобия экспоненциального распределения.
— оценка максимального правдоподобия экспоненциального распределения.
По результатам моделирование построены гистограммы относительных отклонений оценок максимального правдоподобия экспоненциального распределения. По оси ординат отложен процент оценок от общего количества, попавших в данный интервал. Полученные результаты приведены на рис. 1.
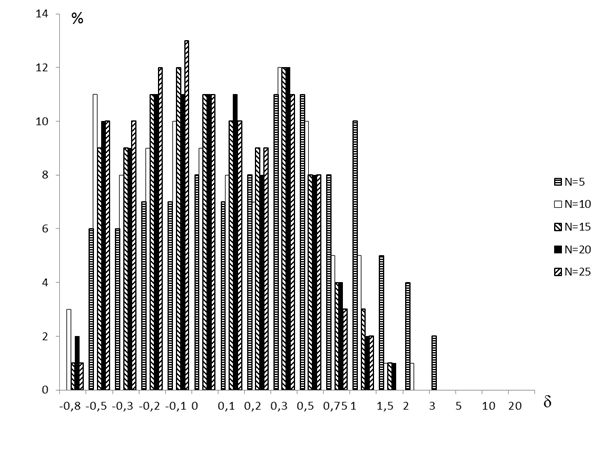
Рис. 1. Относительные отклонения оценки максимального правдоподобия.
Эти экспериментальные данные показывают, что большинство оценок максимального правдоподобия, полученные по малым, однократно цензурированным справа выборкам имеют значительные отклонения от истинных значений. Например, 2 % оценок экспоненциального распределения при N=5 имеют относительные отклонения от 3 до 5; 4 % — относительные отклонения от 2 до 3; 5 % — от 1,5 до 2. С увеличением объема выборки точность оценок возрастает. При N=25 относительные отклонения оценок экспоненциального закона распределения не превышают 1,5. Несмотря на это, 3 % оценок имеют относительные отклонения от 0,75 до 1; 8 % — от 0,5 до 0,75; 11 % — от 0,3 до 0,5.
На рис. 2 показаны графики, проходящие через вершины гистограммы для различных N при общем количестве выборок К=3000.
В целом можно сделать вывод, что точность метода максимального правдоподобия при значениях N < 25 низка. Относительное отклонение оценок от истинных значений может достигать 5 и более, а половина всех оценок имеет отклонения больше 0,3 в зависимости от объема выборки.
В ряде работ [3, 4, 5] проведены исследования, позволяющие установить зависимость точности оценки параметров законов распределения, полученных методом максимального правдоподобия, в зависимости от отдельных характеристик выборки наработок на отказ оборудования. В результате исследований получены зависимости смещения математического ожидания оценки МП от объема выборки N, коэффициента вариации V и степени усечения q. В работе [3] предложен способ введения поправок к оценке МП. Для заданных величин N, V и q по полученным зависимостям определяется смещение dсм оценки МП р'. Несмещенную оценку 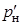 получают по формуле
получают по формуле 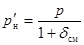 .
.
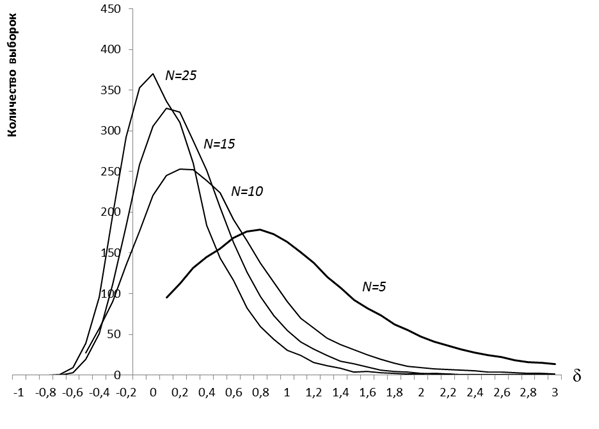
Рис. 2. Гистограммы относительных отклонений, представленные в виде графиков
В перечисленных работах рассматривается влияние на смещение оценки максимального правдоподобия небольшого количества (одного — двух) параметров выборки, что не позволяет глубоко изучить зависимость точности оценки максимального правдоподобия от структуры выборки. При этом дополнительная информация об оценке параметров распределения, содержащаяся в структуре выборки, используется незначительно.
Цель проведенных исследований в общем виде можно сформулировать следующим образом — получение математических моделей, устанавливающих связь между отклонением оценок МП от истинного значения параметра экспоненциального распределения и параметрами, характеризующими структуру выборки.
Решение поставленной задачи осуществлялось в пять этапов:
1. Моделирование на ЭВМ однократно цензурированных справа выборок случайных величин, распределенных по экспоненциальному закону, характерных для плана испытаний [N,U,T], и расчет параметров выборки, характеризующих ее структуру. Для описания структуры сформированной выборки случайных величин в работе использовались стандартные параметры и их производные:
- X1 — степень цензурирования;
- X2 — коэффициент вариации;
- X3 — коэффициент вариации полных случайных величин;
- X4 — эмпирический коэффициент асимметрии;
- X5 — коэффициент эксцесса.
Еще пять параметров представляют собой математические выражения, составленные из стандартных характеристик выборки:
- X6 — отношение математического ожидания полных случайных величин к математическому ожиданию всех членов выборки;
- X7- отношение математического ожидания цензурированных случайных величин к математическому ожиданию всех членов выборки;
- X8- относительное отклонение матожидания от середины вариационного размаха;
- X9 — отношение медианы к математическому ожиданию;
- X10 — отношение моды к математическому ожиданию.
Все параметры измеряются в относительных единицах и не зависят от абсолютных значений случайных величин. Это сделано для того, чтобы можно было применять полученные уравнения к оборудованию со средними наработками на отказ разной величины.
2. Расчет оценок максимального правдоподобия.
3. Расчет зависимого параметра — отклонение оценки максимального правдоподобия от истинного значения по формуле
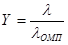 ,
,
4. Построение регрессионных зависимостей. В результате исследований построены регрессионные математические модели, устанавливающие связь между отклонением оценки МП от истинного значения и параметрами, характеризующими структуру выборки. Для каждого объема выборки N построено свое уравнение регрессии.
Математические модели построены в классе линейных уравнений регрессии вида
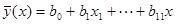 . (2)
. (2)
Полученные уравнения регрессии позволяют повысить точность оценки максимального правдоподобия введением к оценке МП поправки 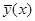 по формуле
по формуле
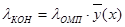 , (3)
, (3)
где 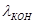 - конечная оценка параметра распределения;
- конечная оценка параметра распределения;
5. В исследованиях была проведена оценка эффективности построенных уравнений регрессии. Для каждой сгенерированной выборки по уравнениям регрессии (2) были рассчитаны поправки к оценке МП и конечная оценка параметра распределения по выражению (3).
Результаты исследований эффективности применения построенных уравнений регрессии для экспоненциального закона распределения показаны на рис. 2 — рис.6.
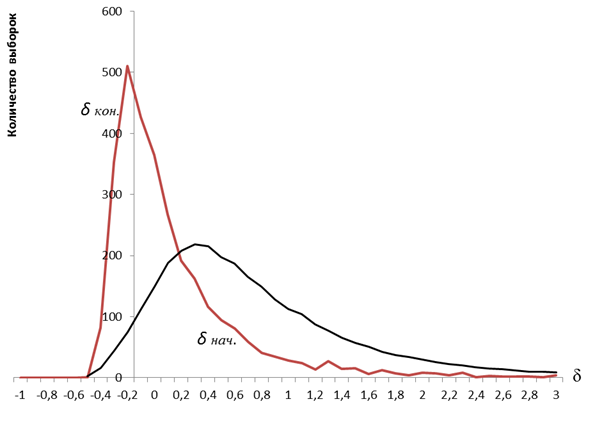
Рис.2. Начальные и конечные отклонения оценок МП для N=5
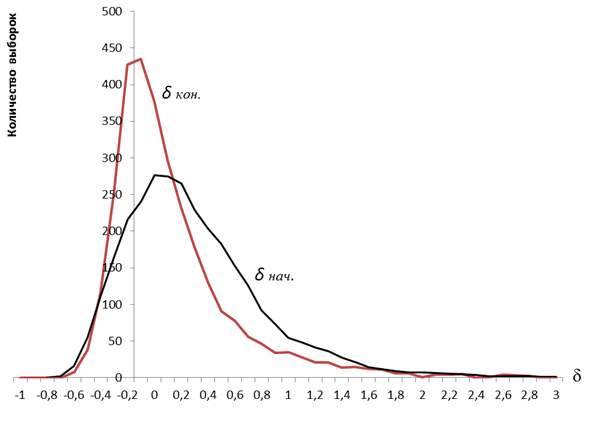
Рис.3. Начальные и конечные отклонения оценок МП для N=10
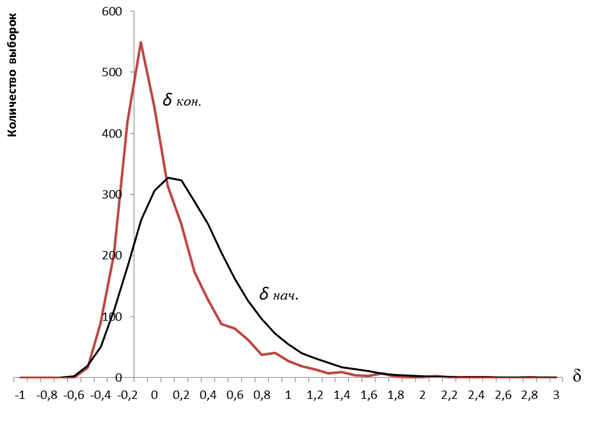
Рис.4. Начальные и конечные отклонения оценок МП для N=15
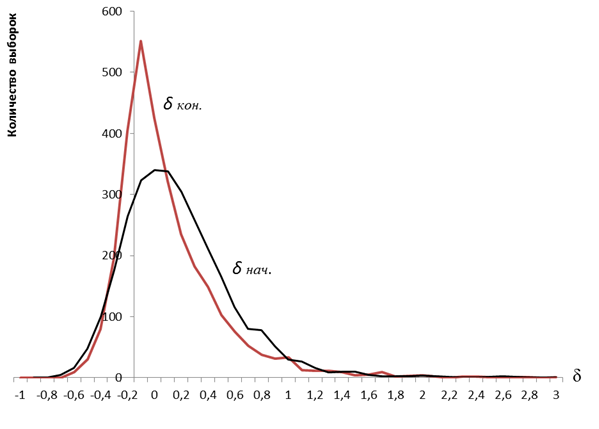
Рис.5. Начальные и конечные отклонения оценок МП для N=20
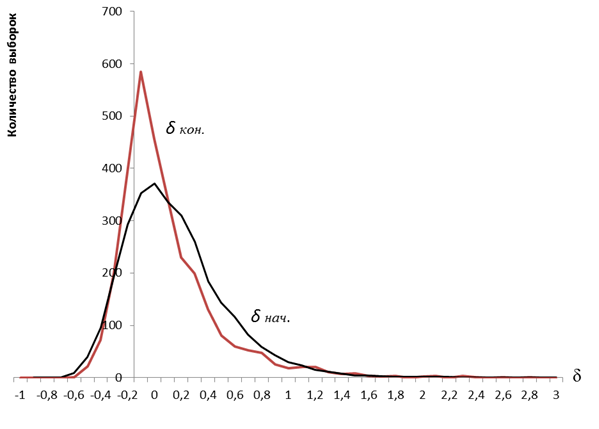
Рис.6. Начальные и конечные отклонения оценок МП для N=25
Графики, приведенные на рис.2 — рис.6 показывают, что точность оценок МП после применения разработанных моделей и введения поправки значительно возрастает. После введения поправки, относительные отклонения оценок от истинного значения параметров распределения, в зависимости от объема выборки N, не превышают 0,3–0,5, в то время как начальные отклонения могут быть больше 3. Наибольший эффект от введения поправок оценкам максимального правдоподобия экспоненциального распределения достигается при числе членов выборки N=5. Окончательно можно сделать вывод о том, что введение поправок позволяет повысить точность оценок максимального правдоподобия, в зависимости от объема выборки, в 2–3 раза.
Литература:
1. ГОСТ 27.410–87. Надежность в технике. Методы контроля показателей надежности и планы контрольных испытаний на надежность. — М: Издательство стандартов, 1987 г.
2. ГОСТ 27.402–95. Планы испытаний для контроля средней наработки до отказа (на отказ). Часть 1. Экспоненциальное распределение. — М: Издательство стандартов, 2002 г.
3. Баталова З. Г., Благовещенский Ю. Н. О точности оценок ресурсов элементов изделий методом максимума правдоподобия при случайном усечении длительностей наблюдений // Надежность и контроль качества.- 1979.- N 9. с.12–20.
4. Бурдасов Е. И., Зарифьянц И. Д., Дворникова Н. Н. Об оценке параметров нормального распределения по случайно цензурированной выборке // Надежность и контроль качества.- 1978.- N 6.- С.10–16.
5. Бурдасов Е. И., Зарифьянц И. Д., Дворникова Н. Н., Аронов И. З. Исследование оценок параметров распределений при анализе результатов незавершенных испытаний.// Надежность и контроль качества, 1980.- N 12. с.47–55.
6. Петрович М. Л., Давидович М. И. Статистическое оценивание и проверка гипотез на ЭВМ.- М.: Финансы и статистика, 1989.189 с.
7. Русин А. Ю. Имитационное моделирование процессов возникновения отказов электрооборудования с целью повышения эффективности системы технического обслуживания и ремонта. Дисс. на соиск. канд. техн. наук. — Тверь: ТГТУ, 1999. 214 с.











