Моделирование физических процессов

Человек издавна использует моделирование для исследования объектов, процессов, явлений в различных областях. Результаты этих исследований служат для определения и улучшения характеристик реальных объектов и процессов; для понимания сути явлений и выработки умения приспосабливаться или управлять ими; для конструирования новых объектов или модернизации старых. Моделирование помогает человеку принимать обоснованные и продуманные решения, предвидеть последствия своей деятельности. [1]

Физика, как учебная дисциплина, предоставляет наиболее широкий спектр применения ЭВТ в качестве средства обучения. Это моделирование физических процессов (демонстрационное и лабораторное), обучающие системы, компьютерный контроль, тренажеры, генераторы индивидуальных заданий при решении задач. Также это могут быть справочно-информационные системы, системы управления экспериментом и, наконец, проведение различных расчетов (в частности, при обработке результатов лабораторного практикума). [2]

Использование компьютера как инструмента учебной деятельности дает возможность переосмыслить традиционные подходы к изучению многих вопросов естественнонаучных дисциплин, усилить экспериментальную деятельность, приблизить процесс обучения к реальному процессу познания, основанному на технологии моделирования. [3]

Решение задач из различных областей деятельности человека на компьютере базируются не только на знаниях технологии моделирования, но, естественно, и на знаниях данной предметной области. Создание компьютерных моделей физических явлений и процессов является одной из эффективных форм реализации практической и исследовательской деятельности учащихся.

Рассмотрим моделирование построения изображения в собирающей и рассеивающей линзе.

Собирающая линза. В средней части толще и отклоняет лучи к оптической оси, если показатель преломления линзы больше показателя преломления среды (рис. 1).

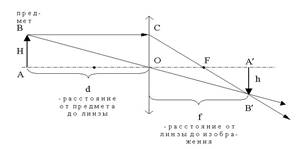
Рис. 1. Собирающая линза

 

Формула тонкой линзы:

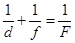                                                                                                                    (1)

находим расстояние от предмета до линзы:

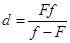                                                                                                                      (2)

расстояние от линзы до изображения:

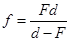                                                                                                                     (3)

здесь d — расстояние от предмета до линзы;

f — расстояние от линзы до изображения

F- фокус

Для нахождения высоты изображения используем формулу (1), выразим из нее h.

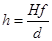                                                                                                                          (4)

где H — высота предмета,

d — расстояние от линзы до предмета,

f — расстояние от линзы до изображения.

Таким образом, что бы найти расстояние от линзы до изображения необходимо воспользоваться формулой (3), а для нахождения высоты изображения формулой (4).

Рассеивающая линза (рис. 2). Формулу рассеивающей линзы можно получить из формулы (1). Для этого условимся считать положительными величины d (от предмета до линзы), f (от линзы до изображения) и F (от линзы до фокуса), если они направлены в сторону падающих лучей. Тогда в формуле (1) для собирающей линзы все члены положительны, для рассеивающей — расстояние от предмета до линзы положительно, d > 0, а расстояния от линзы до изображения и до фокуса отрицательны (f < 0, F < 0). Если перейти к абсолютным значениям расстояний, то получим

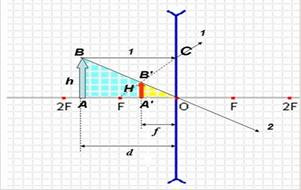
Рис. 2. Рассеивающая линза

 

Для начало в переменные d, h1,f1 считываем данные из соответствующих Edit, при этом переводим значения из строковых величин в числовые.

d:=strtoint(edit1.Text);

Очищаем Image1 для этого свойству Picture присваиваем пустую ссылку

image1.Picture:=nil;

Находим середину Image

x0:=image1.width div 2;

y0:=image1.height div 2;

Для рисования оси Ox устанавливаем у карандаша цвет серый и толщину пера 2.

Pen.Color:=clSilver;

Pen.Width:=2;

С помощью процедур MoveTo и LineTo строим ось Ox MoveTo(10, y0); LineTo(2*x0–10, y0);

Далее меняем цвет пера на синий и строим линзу в зависимости от выбранной линзы: рассеивающую и собирающую.

Pen.Color:=clBlue;

if radiogroup1.ItemIndex =0 then

with image1.Canvas do

begin

MoveTo(x0, 20); LineTo(x0, 2*y0–20);

MoveTo(x0, 20); LineTo(x0–5, 10);

MoveTo(x0, 20); LineTo(x0+5, 10);

MoveTo(x0, 2*y0–20); LineTo(x0+5,2*y0–10);

MoveTo(x0, 2*y0–20); LineTo(x0–5,2*y0–10);

end

else begin

with image1.Canvas do

begin

MoveTo(x0, 10); LineTo(x0, 2*y0–10);

MoveTo(x0, 10); LineTo(x0–5, 20);

MoveTo(x0, 10); LineTo(x0+5, 20);

MoveTo(x0, 2*y0–10); LineTo(x0+5,2*y0–20);

MoveTo(x0, 2*y0–10); LineTo(x0–5,2*y0–20);

end;

После построения линзы строим 2 луч. Первый луч проходит через вершину объекта и параллелен оси Ox, второй луч проходит через вершину объекта и центр линзы.

MoveTo(x0-d,y0-h1); LineTo(x0–1,y0-h1);

MoveTo(x0–5,y0-h1–3); LineTo(x0–1,y0-h1);

MoveTo(x0–5,y0-h1+3); LineTo(x0,y0-h1);

MoveTo(x0-d,y0-h1); LineTo(x0+d,y0+h1);

MoveTo(x0+d,y0+h1); LineTo(x0+d-2,y0+h1–7);

MoveTo(x0+d,y0+h1); LineTo(x0+d-7,y0+h1+1);

И строим луч, проходящий через фокус и точку пересечения луча параллельного оси Ox и линзы. При этом стиль линий меняем на штрихпунктирный

pen.Style:=psDot;

MoveTo(x0-f1,y0);LineTo(x0,y0-h1);

pen.Style:=psSolid;

MoveTo(x0,y0-h1);LineTo(x0+f1 div 4,y0-h1-h1 div 4);

MoveTo(x0+f1 div 4,y0-h1-h1 div 4);

LineTo(x0+f1 div 4–7,y0-h1-h1 div 4+2);

MoveTo(x0+f1 div 4,y0-h1-h1 div 4);

LineTo(x0+f1 div 4–2,y0-h1-h1 div 4+7);

Далее строим объект в виде стрелочки, и заливаем его синим цветом.

MoveTo(x0-d+3,y0); LineTo(x0-d+3,y0-h1+6);

MoveTo(x0-d-3,y0); LineTo(x0-d-3,y0-h1+6);

MoveTo(x0-d+3,y0-h1+6); LineTo(x0-d+7,y0-h1+6);

MoveTo(x0-d-3,y0-h1+6); LineTo(x0-d-7,y0-h1+6);

MoveTo(x0-d-7,y0-h1+6); LineTo(x0-d,y0-h1);

MoveTo(x0-d+7,y0-h1+6); LineTo(x0-d,y0-h1);

MoveTo(x0-d-3,y0); LineTo(x0-d+3,y0);

Brush.Color:=clBlue;

FloodFill(x0-d,y0–5,clBlack, fsBorder);

Для построения изображения вначале находи высоту изображения и расстояние до него от линзы.

f2:=round(1/(1/d+1/f1));

h2:=round(h1*f2/d);

После этого строим изображение и закрашиваем его красным цветом

MoveTo(x0-f2+3,y0); LineTo(x0-f2+3,y0-h2+4);

LineTo(x0-f2+5,y0-h2+4);

LineTo(x0-f2,y0-h2);

MoveTo(x0-f2–3,y0); LineTo(x0-f2–3,y0-h2+4);

LineTo(x0-f2–5,y0-h2+4);

LineTo(x0-f2,y0-h2);

MoveTo(x0-f2–3,y0); LineTo(x0-f2+3,y0);

Brush.Color:=clRed;

FloodFill(x0-f2,y0–5,clBlack, fsBorder);

Построения изображения для рассеивающий линзы происходит аналогичным образом.

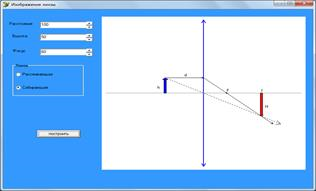
Рис. 3. Интерфейс приложения для изображения в тонкой линзе

 

Литература:

 

1.         Особенности компьютерного моделирования. (http://life-prog.ru/1_14515_osobennosti-kompyuternogo-modelirovaniya.html)

2.         Ахметов A. K., Калманова Д. М., Мендалиева Ш. О. «Компьютерное моделирование физических процессов». (http://www.rusnauka.com/14_NPRT_2011/Informatica/3_87168.doc.htm)

3.                  Компьютерное моделирование и реальный эксперимент на уроках физики как повышение мотивации к изучению предмета. (http://nsportal.ru/shkola/fizika/library/2012/01/28/kompyuternoe-modelirovanie-i-realnyy-eksperiment-na-urokakh-fiziki)