Расчет распределения тока в плоском индукционном нагревателе с емкостной связью
Авторы: Захарова Евгения Игоревна, Науман Ольга Александровна, Захаров Игорь Вячеславович
Рубрика: 4. Электротехника
Опубликовано в
III международная научная конференция «Актуальные вопросы технических наук» (Пермь, апрель 2015)
Дата публикации: 05.02.2015
Статья просмотрена: 315 раз
Библиографическое описание:
Захарова, Е. И. Расчет распределения тока в плоском индукционном нагревателе с емкостной связью / Е. И. Захарова, О. А. Науман, И. В. Захаров. — Текст : непосредственный // Актуальные вопросы технических наук : материалы III Междунар. науч. конф. (г. Пермь, апрель 2015 г.). — Пермь : Зебра, 2015. — С. 70-76. — URL: https://moluch.ru/conf/tech/archive/125/7324/ (дата обращения: 24.04.2025).
Проблема снижения реактивной мощности электротехнических нагревательных устройств возможна за счет совмещения свойств электрического нагрева и повышения собственного Cos j установки. Примером такого совмещения может служить плоский индуктор с емкостной связью [1], позволяющий отказаться от средств искусственной компенсации, составляющих до третьей части индукционной установки в целом.
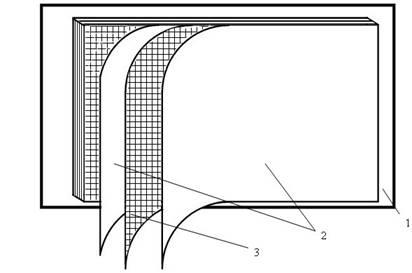
Рис. 1. Эскиз системы «плоский индукционный нагреватель с емкостной связью — нагреваемая поверхность»: 1 — нагреваемая поверхность; 2- разноименные проводниковые ленты; 3 — диэлектрическая лента
В самом простом случае конструкция, поясняющая принцип действия включает в себя следующее. Два проводника одной полярности соединены между собой и между ними размещен третий проводник противоположной полярности (в другом случае не три, а n проводников). Проводники изолированы друг от друга слоем диэлектриком.
Токи в ленточных проводниках имеют одинаковое направление, а магнитные поля, создаваемые этими токами складываются. Ток в ленточных проводниках существует в виде тока проводимости и замыкается через диэлектрик в виде тока смещения. Интенсивность суммарного магнитного поля зависит от числа витков и тока индуктора и выбирается исходя из активной мощности, требуемой для нагрева загрузки.
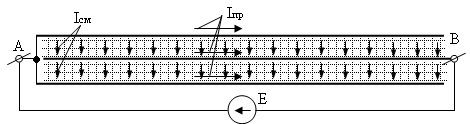
Рис. 2. Принципиальная упрощенная схема устройства
Для получения значений токов (в данном случае — I1, I2, I3) в проводниках устройства рассмотрим схему, изображенную на рисунке 3. Анализ показал, что наиболее эффективным будет получение итогового решения по методу контурных токов.
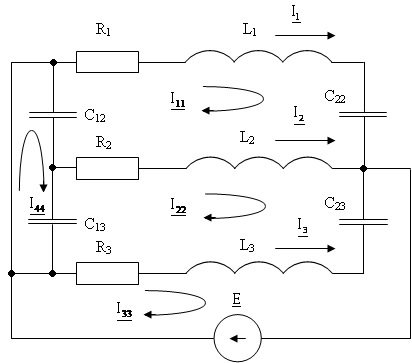
Рис. 3. Электрическая схема замещения устройства
Задаемся направлением токов ветвей и обозначаем их на схеме. Произвольно выбираем направление действительных токов в прооводниках (I1, I2, I3). Затем выделяем четыре контура и указываем направление контурных токов I11, I22, I33, I44. Направление контурных токов принимаем по часовой стрелке. Далее определяем собственные и взаимные сопротивления элементов схемы. Расчеты проводим по известным (2,3) формулам.
При расчете индуктивности обмотки необходимо учитывать, что плотность тока в аксиальном направлении уменьшается от места ввода тока к периферии, т. е. jа = f(x). Таким образом, индуктивность плоской секции L1, Гн, можно считать эквивалентной проводнику прямоугольного сечения, имеющего те же размеры, что и секция и рассчитать по формуле (2)
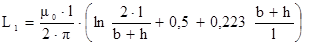 , (1)
, (1)
где l – длина секции, см;
h – высота секции, см;
b – толщина секции, см.
Так как все проводники секции индуктора работают в электромагнитном поле, созданном током индуктора, то взаимное влияние этих проводников друг на друга определится как взаимная индуктивность двух одинаковых прямоугольников с параллельными сторонами
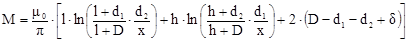 (2)
(2)
где d– толщина диэлектрика, см.
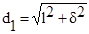 , (3)
, (3)
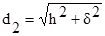 , (4)
, (4)
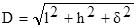 . (5)
. (5)
Собственная емкость секции индуктора С1, пФ, рассчитывается по формуле (3) для плоской многопластинчатой секции, собранной из N проводников, соединенных через один параллельно
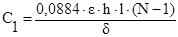 . (6)
. (6)
Активное сопротивление R, Ом определяется по формуле
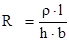 , (7)
, (7)
где r – удельное электрическое сопротивление материала проводника, Ом м.
Определяем независимые контуры и их нумеруем. При наличии в схеме источников тока независимые контуры, для которых составляем уравнения метода контурных токов, можно определить, если мысленно удалить источники тока. Выбираем направление контурных токов (целесообразно в одну сторону) и составляем уравнения по методу контурных токов, обходя каждый контур в направлении его контурного тока. Контурный ток, проходящий через источник тока, известен и равен току источника тока (через источник тока проходит только один контурный ток). Полученную систему алгебраических уравнений решаем относительно неизвестных контурных токов.
Составляем систему уравнений контурных токов. В левой части уравнений входят падения напряжений в контуре, а в правой ЭДС данного контура.
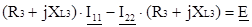
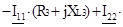
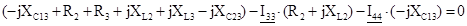
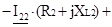
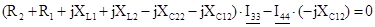 (8)
(8)
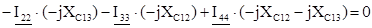
Определители системы уравнений (8)
D = 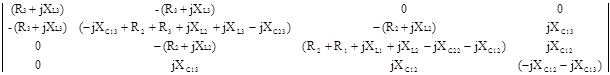
D1 = 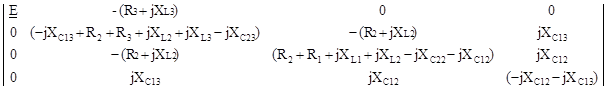
D2 = 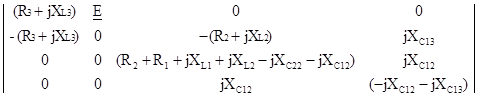
D3 = 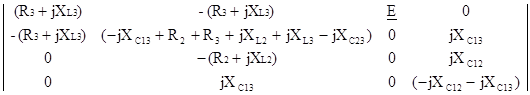
D4 = 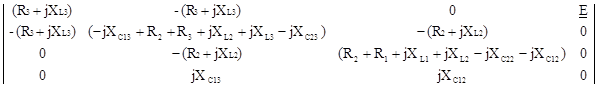
Токи в контурах с 1 по 4 определяются как
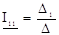 ;
; 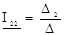 ;
; 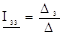 ;
; 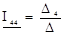 .
.
Токи в проводниках индукционного нагревателя определяются как
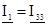 ;
; 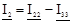 ;
; 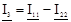 .
.
Представленная методика расчета реализована в виде программы REZCUR (рисунок 4), созданной в программной среде Borland DELPHI.
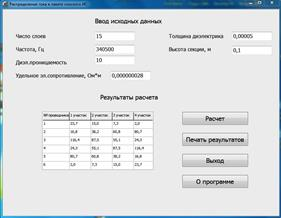
Рис. 4. Панель исполнительного модуля программы «REZCUR»
С использованием указанной программы проведен расчет распределения тока в проводниках и диэлектрике плоского индуктора с емкостной связью.
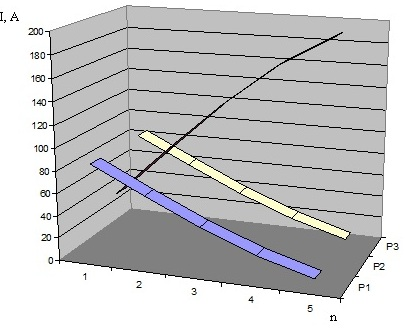
Рис. 5. Зависимость изменения тока I по длине проводников L (n) плоского индуктора с емкостной связью при трехпроводниковой конструкции
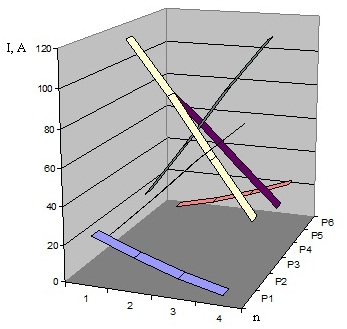
Рис. 6. Зависимость изменения тока I по длине проводников L (n) плоского индуктора с емкостной связью при шестихпроводниковой конструкции
При исследовании распределения тока по длине проводниковых лент замечена симметрия, ось которой проходит по центральной части конструкции: в случае нечетного количества проводников — по центральному проводнику, в случае четного количества проводников — между двумя центральными проводниками. При этом конструкция условно делится на верхнюю и нижнюю идентичные части (рис. 5, рис. 6).
Изменение тока, как в его нарастании, так и в снижении происходит в основном линейно. Некоторая нелинейность замечена в правой части конструкции.
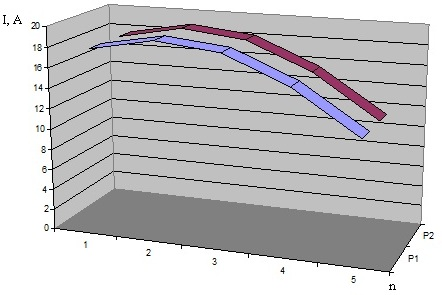
Рис. 7. Зависимость изменения тока I в диэлектрике по его длине L (n) в плоском индукторе с емкостной связью при трехпроводниковой конструкции
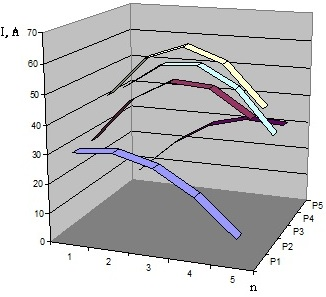
Рис. 8. Зависимость изменения тока I в диэлектрике по его длине L (n) в плоском индукторе с емкостной связью при шестипроводниковой конструкции
Наиболее токонагруженная часть устройства включает в себя проводники из центральной зоны конструкции. Остальные проводники попарно взаимно-противоположно уменьшают токовые значения до периферии.
Характерно, что сумма токовых значений в пределах одной зоны проводников есть величина постоянная по всей их длине, т. е. 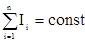 .
.
При исследовании распределения тока по длине диэлектрика конструкции также отмечена симметрия, ось которой проходит по центральной части конструкции (рис. 7, рис. 8). В трехпроводниковой конструкции ток в диэлектрике от входа несколько увеличивается, затем снижается до конца диэлектрика. Существенная токонагруженность соответствует 2/5 всей длины диэлектрика. В конструкции, представленной на рис.8, центральная значительно токонагруженная часть приходится на среднюю зону с ярко выраженным максимумом.
Таким образом, исследования помогли выяснить, что наиболее токонагруженная зона конструкции приходится на центральную ее часть. Этот фактор необходимо учитывать при проектировании устройства с целью обеспечения допустимого теплового режима.
Литература:
1. Мухаметшин Р. Р., Науман О. А., Захаров И. В. Исследование резонансного режима плоских индукционных систем с емкостной связью. Технические науки в России и за рубежом: материалы III Mеждународной научной конференции, Москва, 2014. — М.: Буки-Веди, 2014.
2. Калантаров П. Л., Цейтлин Л. А. Расчет индуктивностей: Справочная книга. — Л.: Энегоатомиздат. Ленингр. отд-ние, 1986.
3. Расчет электрической емкости/Ю. Я. Иоссель, Э. С. Кочанов, М. Г. Струнский. — Л.: Энергоиздат, Ленингр. отд-ние,1981.











