Методы приближения функций параболическими сплайнами
Автор: Рахимов Бахтияр Саидович
Рубрика: 3. Автоматика и вычислительная техника
Опубликовано в
III международная научная конференция «Актуальные вопросы технических наук» (Пермь, апрель 2015)
Дата публикации: 08.04.2015
Статья просмотрена: 592 раза
Библиографическое описание:
Рахимов, Б. С. Методы приближения функций параболическими сплайнами / Б. С. Рахимов. — Текст : непосредственный // Актуальные вопросы технических наук : материалы III Междунар. науч. конф. (г. Пермь, апрель 2015 г.). — Пермь : Зебра, 2015. — С. 65-67. — URL: https://moluch.ru/conf/tech/archive/125/7351/ (дата обращения: 24.04.2025).
Значительное место при обработке результатов наблюдений занимают задачи интерполяции и аппроксимации данных измерений, заданных на дискретных сетках (обычно в форме таблиц отсчетов). Теория интерполяции функций полиномами целых неотрицательных степеней
P(x) = a0+ a1x + a2x2+ … + amxm (1)
где ai — коэффициенты полинома (i = 0, 1, …, m), m — степень полинома, дает нам один из наиболее широких классов математических моделей процессов.
Вместе с тем для многих традиционных задач построения полиномов высоких степеней m, интерполирующих одной «глобальной» формулой заданные функции в узлах отрезка конечной длины, характерны малоприятные явления, заключающиеся в быстром росте величин ошибок между узлами интерполяции с ростом степени полиномов. Они ведут к тому, что отсутствует сходимость интерполирующих полиномов к функции.
Оценки точности приближения функций кусочно-полиномиальными интерполянтами зависят от дифференциальных свойств интерполируемых функций, от их гладкости и от способа разбиения на малые интервалы полного отрезка [a,b], на котором задана функция f(x). Создается сетка узлов интерполяции
a£ x0< x1< … <xi< … <xn£ b, (2)
которая является равномерной, если шаг интерполяции h выбирается по формуле
h= xi+1 — xi= const, (3)
и становится неравномерной, если разбиение отрезка производится на интервалы произвольной длины.
Оценки максимальных значений ошибок интерполяции кусочными полиномами различных степеней в литературе по численному анализу получены в результате исследования остаточных членов формул для полиномов, построенных в соответствии с методами Ньютона и Лагранжа. Если метрика задана в пространстве С(m), то имеют место следующие неравенства для кусочных полиномов различных степеней [3,8]:
1) для полиномов нулевой степени (кусочно-постоянных функций):
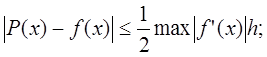 (4)
(4)
2) для полиномов 1-й степени (ломаных или кусочно-линейных функций):
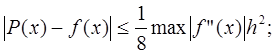 (5)
(5)
3) для полиномов 2-й степени (кусочно-квадратических функций):
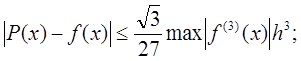 (6)
(6)
4) для полиномов 3-й степени (кусочно-кубических функций):
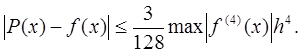 (7)
(7)
В случае не равноотстоящих узлов неравенства (4) — (7) также пригодны для оценки точности интерполяции. Отличие состоит в том, что в правые части выражений подставляется максимальное значение шага hmax.
Недостатком методов интерполяции кусочными полиномами является отсутствие гладкости интерполянтов в некоторых точках, поскольку имеют место разрывы производных в узлах. Приведем здесь математическое определение понятия гладкой функции [3].
Функция f(x) называется гладкой на отрезке [a,b], если она непрерывна на этом отрезке и имеет на нем непрерывную производную f’(x).
Наряду с этим определением с целью подчеркнуть способность функций к многократному непрерывному дифференцированию, употребляется термин «степень гладкости». Он означает величину порядка наивысшей производной, которая непрерывна на данном отрезке.
Введем еще несколько необходимых определений:
Функция f(x) называется кусочно-непрерывной на отрезке [a,b], если она определена и непрерывна всюду на [a,b], за исключением, быть может, конечного числа точек xi(a< x1<x2< …< xn< b), в которых существуют пределы f справа и слева. Таким образом, кусочно-непрерывная на [a,b] функция непрерывна на каждом из интервалов (xi, xi+1).
Функция f(x) называется кусочно гладкой на отрезке [a,b], если она кусочно-непрерывна и имеет кусочно непрерывную производную f’(x) на этом отрезке.
Частным случаем кусочно-гладкой функции является непрерывная кусочно гладкая на отрезке [a,b] функция. Она представляет собой функцию, которая непрерывна на [a,b], и кроме того, существует разбиение отрезка на частичные отрезки [xi,xi+1], при котором функция является гладкой на каждом из этих отрезков.
Понятие гладкости тесно связано с понятием кривизны и радиуса кривизны. Если функция f(x) в окрестности точки x имеет непрерывную производную и в самой точке вторую производную, то радиус кривизны подчиняется следующему соотношению [6]:
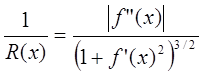 . (8)
. (8)
Кривизной радиуса R называется число 1/R. При малых значениях f’(x) (f’<<1) радиус приближенно равен R(x)@1/f”(x).
Сплайны как класс кусочных функций вследствие ряда преимуществ перед другими методами аппроксимации находят все более широкое применение при разработке аппаратных и программных средств анализа и восстановления сигналов, расширяя рамки традиционных подходов к приближению функций [3,4].
К этим преимуществам относятся:
- устойчивость сплайнов относительно локальных возмущений, в отличие от полиномиальной интерполяции;
- хорошая сходимость сплайн-интерполяции в отличие от интерполяции многочленами;
- экстремальные свойства сплайнов. Сплайны обеспечивают значения функционалов, доставляющими минимальную гладкость функций в гильбертовом пространстве и в пространстве ограниченных функций.
- построение интерполяционных сплайнов сводится к решению ленточных (квазидиагональных) систем линейных алгебраических уравнений (СЛАУ), для которых в численном анализе разработаны эффективные методы и алгоритмы решений.
Понятие «сплайн» происходит от английского слова «spline», что в чертежном деле означает в переводе «рейка, гибкая линейка». Если разбить отрезок [a,b] оси абсцисс точками a=x0<x1<…<xn=b, называемыми узлами сетки, на интервалы [xi,xi+1], то определение сплайна можно привести в следующей форме:
полиномиальным сплайном степени m называется функция Sm(x), обладающая следующими свойствами [7–10]:
1) функция Sm(x) непрерывна на отрезке [a,b] вместе со всеми своими производными до некоторого порядка r;
2) на каждом интервале [xi,xi+1] функция Sm(x) совпадает с алгебраическим полиномом Pm,i(x) степени m:
Sm(x) = Pm,i(x) = ao,i + a1,i(x-xi) + a2,i(x-xi)2 +…+ am,i(x-xi)m (9)
Разность между степенью сплайна и наивысшим порядком r (m-r целое число) непрерывной на отрезке [a,b] производной называется дефектом сплайна [3].
Литература:
1. Агевич С. Н. Сплайн-Виленкина-Крестенсона функции в представлении сигналов./Научное приборостроение. 2002, Т. 12, № 1, С.79–89.
2. Алгоритмы и программы восстановления зависимостей /Под.ред. В. Н. Вапника. -М.: Наука, 1984. — 816 с.
3. Ахмед Н., Рао К. Ортогональные преобразования при обработке цифровых сигналов. -М.: Связь, 1980. — 248 с.
4. Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. Численные методы. М.: Наука, 1987.
5. Верлань А. Ф., Абдусаттаров Б. Б., Акбаров Ш. А. Алгоритмические и структурные методы повышения быстродействия специализированных устройств при реализации интегральных моделей нелинейных динамических объектов // Электронное моделирование. — 1987. — № 6. — С. 42–44.
6. Зайнидинов Х. Н., Алгоритмы быстрых спектральных преобразований и их применение для восстановления сигналов. // Актуальные проблемы радиотехники, электроники и связи. (Секция вычислительной техники). Тезисы докл. научн. — техн. конференции. Санкт-Петербург, 1992 С.
7. Зайнидинов Х. Н., Рахимов Б. С. Хамдамов У. Р. Программный комплекс для обработки одномерных и многомерных геофизических сигналов в кусочно — полиномиальных базисах.// Совместный выпуск по материалам респ. науч. конф. «Современное состояние и пути развития информационных технологий» 11–13 октября 2006, г.Ташкент, с.205–207
8. Касымов С. С., Зайнидинов Х. Н., Рахимов Б. С. Аппаратно — ориентированный алгоритм вычисления коэффициентов в кусочно — квадратических базисах // ДАН РУЗ. 2003. № 3, -С. 18–21.
9. Касымов С. С., Зайнидинов Х. Н., Рахимов Б. С. Применение базисных сплайнов для предварительной обработки экспериментальных данных // Тезисы докл. XVI — Международная научная конф., Санкт — Петербург, 2003.
10. Малоземов В. Н., Певный А. Б. Дискретные периодические B-сплайны // Вестник СПбГУ. Сер. 1. 1997. Вып. 4 (№ 22). С. 14–19.
11. Микропроцессорных комплект БИС серии К 1815 для цифровой обработки сигналов: Справочник /А. И. Белоус, О. В. Подрубный, В. М. Журба; под ред. А. И. Сухопарова. — М.: Радио и связь, 1992. — 256 с.
12. Мусаев М. М., Ходжаев Л. К. Спектральный метод полиномиальной аппроксимации для цифровой обработки сигналов.// Электронное моделирование. — 1987. -N6, — С. 30–33.
13. Ракощиц В. С., Козлов А. В., Можаев И. А. и др. Специализированные микропроцессоры, реализующие быстрые преобразования // Цифровая обработка сигналов: сб. статьей. — М.: Наука, 1981. — С. 206–217.
14. Рахимов Б. С. Применение кусочно — постоянных, кусочно — линейных и кусочно — квадратических базисных функций Уолша для спектральной обработки сигналов. // Тезисы докл. сб. науч. статьей., Ташкент, -С 319–320.
15. Рахимов Б. С. Проектирование спецпроцессов для обработки сигналов на основе матричной диаграммы занятности.// Научно — технический журнал Ферганского политехнического института. 2003, № 4, — С 31–34.
16. Рахимов Б. С. Кусочно — полиномиальные методы на основе функций Уолша.// Актуальные вопросы в области технических и социально-экономических наук. Межвузовский сб. научн. трудов. Ташкент 2006, вып.1., — С. 42–43.
17. Смолов В. Б., Свиньин С. Ф., Зенцов В. А. Аппроксимация системами кусочно-полиномиальных функций в задачах цифровой обработки сигналов. //Изв.АН СССР, Техническая кибернетика, 1982. — N2. -С. 202–209.
18. Kasymov S. S., Zaynidinov H. N., Rahimov B. S. Methods of the organization of parallel computing structures and processes on the basics of basic splines // Proceedings of the 1st Seminar «The opportunities for Application of Information Technologies for Development of Education and Economic Growth». Tashkent, july 3–5, 2003., p. 97–98.











