Анализ методов вычисления коэффициентов приближения параболическими сплайнами
Авторы: Рахимов Бахтияр Саидович, Собирова Сабохат Кабуловна, Кадирова Наргиза Илхомбаевна
Рубрика: 3. Автоматика и вычислительная техника
Опубликовано в
III международная научная конференция «Актуальные вопросы технических наук» (Пермь, апрель 2015)
Дата публикации: 08.04.2015
Статья просмотрена: 330 раз
Библиографическое описание:
Рахимов, Б. С. Анализ методов вычисления коэффициентов приближения параболическими сплайнами / Б. С. Рахимов, С. К. Собирова, Н. И. Кадирова. — Текст : непосредственный // Актуальные вопросы технических наук : материалы III Междунар. науч. конф. (г. Пермь, апрель 2015 г.). — Пермь : Зебра, 2015. — С. 62-65. — URL: https://moluch.ru/conf/tech/archive/125/7720/ (дата обращения: 03.04.2025).
Построение полиномиальных интерполяционных сплайнов Sm(x) степени m ³ 2 связано с решением СЛАУ определенного вида, причем важную роль играют дополнительные условия, возникающие на концах интервалов и называемые поэтому краевыми или граничными [1,3]. Без их учета система уравнений получается не полностью определенной, так как тогда число уравнений, равное n-1, получается меньшим, чем число неизвестных, которое равно n+1.
На практике при интерполяции сплайнами обычно задаются следующие варианты граничных условий [3,2,8]:
1) Если в граничных точках известны значения первой производной f’(a) и f’(b), то естественно положить S’0 = f’(a) и S’n = f’(b). Добавление этих условий приводит к системе, которая может быть решена одним из эффективных методов, например методом прогонки [2, 7, 8].
2) Если на концах интервала известны значения второй производной f’’(a) и f’’(b), то их можно принять в качестве граничных значений на значения второй производной сплайна S’’m(a) и S’’m(b) в этих же точках.
3) Если задать граничные условия f’’(a) = f’’(b) = 0, то получается система алгебраических уравнений, соответствующих так называемому естественному сплайну.
4) Если нет никакой дополнительной информации о значениях производных от функции на концах отрезка, то используется так называемое условие «отсутствия узла». Выбор наклонов S’i производится таким образом, чтобы сплайн на втором интервале являлся продолжением сплайна, строящегося на первом интервале, а сплайн на интервале с номером n соответственно стал продолжением сплайна, заданного на интервале с номером n-1. Для этого достаточно потребовать совпадения в узлах x1 и xn-1 значений третьих производных:
S(3)1(x1) = S(3)2(x1), S(3)n-1(xn-1) = S(3)n(xn-1). (1)
Важную роль в алгоритмах вычисления параметров аппроксимации функций сплайнами играют свойства матриц коэффициентов систем соответствующих алгебраических уравнений. В частности, фактором, определяющим существование и устойчивость решения, является свойство диагонального доминирования (преобладания).
Так как функции Вm,i(X), линейно независимы и на отрезке [a, b] являются сплайнами степени m с узлами в точках сетки, то любой сплайн Sm(X) из Sm,i(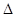 ) можно единственным образом представить в виде
) можно единственным образом представить в виде
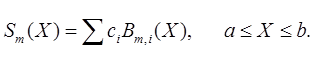
 (2)
(2)
Дополним сетку точками 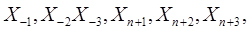 :
:

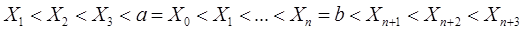
Например, можно положить 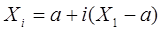 i=-1, -2, -3,
i=-1, -2, -3, 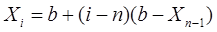 i=n+1, n+2, n+3.Пусть
i=n+1, n+2, n+3.Пусть


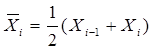 , i =-2, -1, 0, 1, …, n+3.
, i =-2, -1, 0, 1, …, n+3.
Качестве 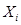 в общем случае можно выбрать точки, удовлетворяющие неравенствам
в общем случае можно выбрать точки, удовлетворяющие неравенствам

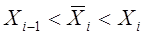 , i =-2, -1, 0, 1, …, n+3.
, i =-2, -1, 0, 1, …, n+3.
Мы дадим здесь представление интерполяционных параболических сплайнов через В-сплайны, определяемые равенством при m=3
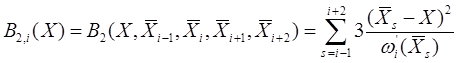 ,
,
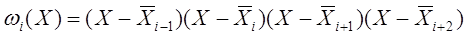
Как указывалось, любой сплайн 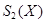 , определенной на [а,в] и имеющий узлы
, определенной на [а,в] и имеющий узлы 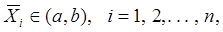 единственным образом представим в виде
единственным образом представим в виде
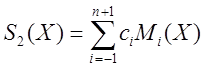 (3)
(3)
где
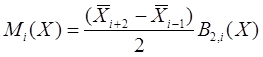 (4)
(4)
в отличие от (1), мы воспользовались представлением через Мi(X), а не через В2,i(X) в силу при 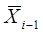 , близком к
, близком к 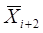 , функция В2,i(X) принимает в некоторых точках большие значения, порядка
, функция В2,i(X) принимает в некоторых точках большие значения, порядка 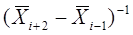 , а в дальнейшем расстояние между узлами будет уменьшаться. Как будет видно из дальнейшего, коэффициенты сi в (5) будут близки к значениям интерполируемой функции в соответствующих точках.
, а в дальнейшем расстояние между узлами будет уменьшаться. Как будет видно из дальнейшего, коэффициенты сi в (5) будут близки к значениям интерполируемой функции в соответствующих точках.
Удобства представления (5) заключается в том, что для запоминания 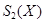 можно хранить лишь множества
можно хранить лишь множества 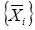 и
и 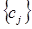
Исходя из условий интерполяции и краевых условий, выведем системы уравнений для определения коэффициентов сi в (5). Учитывая свойства (6) имеем
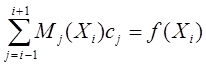 , i = 0, 1, …, n (5)
, i = 0, 1, …, n (5)
Краевые условия добавляют к (7) следующие уравнения:
А) периодический случай
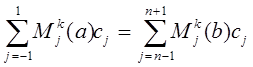 k=1,2; (6)
k=1,2; (6)
Б) краевые условия (5):
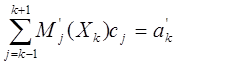 k=0,n;
k=0,n; 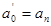
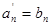 (7)
(7)
B) краевые условия (6):
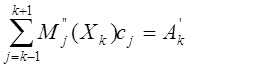 k=0,n;
k=0,n; 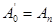
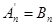 (8)
(8)
Г) краевые условия (7):
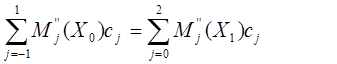
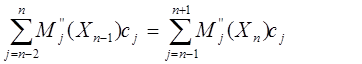 (9)
(9)
Уравнения (7) вместе с двумя уравнениями характеризующими краевые условия, дают систему 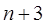 уравнений с
уравнений с 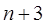 неизвестными. Определитель этой системы отличен от нуля, так как в силу единственности представления (5) система имеет единственное решение.
неизвестными. Определитель этой системы отличен от нуля, так как в силу единственности представления (5) система имеет единственное решение.
Достоинством интерполяционных сплайнов является их высокая точность, а недостаток — необходимость решения систем уравнений, что связано с большим временными затратами. Для систем, функционирующих в реальном масштабе времени актуальны те методы, которые позволяют избегать решение систем уравнений.
Значительно упрощаются вычислительные проблемы при обращении к методам локальной сплайн — аппроксимации, в которых значения приближающей функции на каждом отрезке зависят только от значений аппроксимируемой функции из некоторой окрестности этого отрезка. Необходимый объем вычислений не зависит от числа узлов сетки, а определяется лишь степенью сплайна [4,12].
Для параболических базисных сплайнов приведем локальные формулы в готовом виде:
1. Трехточечная формула
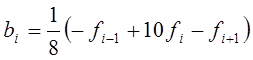
2. Пятиточечная формула

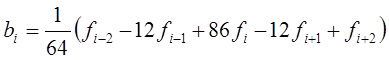
Эти формулы сохраняют свойства гладкости приближений, а значения параметров не зависят от отсчетов в точках, достаточно удаленных от текущей точки с индексом i. Они являются симметричными, но работают только внутренних точках области [a,b].
Литература:
1. Ахмед Н., Рао К. Ортогональные преобразования при обработке цифровых сигналов. -М.: Связь, 1980. — 248 с.
2. Верлань А. Ф., Абдусаттаров Б. Б., Акбаров Ш. А. Алгоритмические и структурные методы повышения быстродействия специализированных устройств при реализации интегральных моделей нелинейных динамических объектов // Электронное моделирование. — 1987. — № 6. — С. 42–44.
3. Зайнидинов Х. Н., Рахимов Б. С. Хамдамов У. Р. Программный комплекс для обработки одномерных и многомерных геофизических сигналов в кусочно — полиномиальных базисах.// Совместный выпуск по материалам респ. науч. конф. «Современное состояние и пути развития информационных технологий» 11–13 октября 2006, г.Ташкент, с.205–207
4. Касымов С. С., Зайнидинов Х. Н., Рахимов Б. С. Аппаратно — ориентированный алгоритм вычисления коэффициентов в кусочно — квадратических базисах // ДАН РУЗ. 2003. № 3, -С. 18–21.
5. Касымов С. С., Зайнидинов Х. Н., Рахимов Б. С. Применение базисных сплайнов для предварительной обработки экспериментальных данных // Тезисы докл. XVI — Международная научная конф., Санкт — Петербург, 2003.
6. Мусаев М. М., Ходжаев Л. К. Спектральный метод полиномиальной аппроксимации для цифровой обработки сигналов.// Электронное моделирование. — 1987. -N6, — С. 30–33.
7. Ракощиц В. С., Козлов А. В., Можаев И. А. и др. Специализированные микропроцессоры, реализующие быстрые преобразования // Цифровая обработка сигналов: сб. статьей. — М.: Наука, 1981. — С. 206–217.
8. Рахимов Б. С. Применение кусочно — постоянных, кусочно — линейных и кусочно — квадратических базисных функций Уолша для спектральной обработки сигналов. // Тезисы докл. сб. науч. статьей., Ташкент, -С 319–320.
9. Рахимов Б. С. Проектирование спецпроцессов для обработки сигналов на основе матричной диаграммы занятности.// Научно — технический журнал Ферганского политехнического института. 2003, № 4, — С 31–34.
10. Рахимов Б. С. Кусочно — полиномиальные методы на основе функций Уолша.// Актуальные вопросы в области технических и социально-экономических наук. Межвузовский сб. научн. трудов. Ташкент 2006, вып.1., — С. 42–43.
11. Смолов В. Б., Свиньин С. Ф., Зенцов В. А. Аппроксимация системами кусочно-полиномиальных функций в задачах цифровой обработки сигналов. //Изв.АН СССР, Техническая кибернетика, 1982. — N2. -С. 202–209.
12. Kasymov S. S., Zaynidinov H. N., Rahimov B. S. Methods of the organization of parallel computing structures and processes on the basics of basic splines // Proceedings of the 1st Seminar «The opportunities for Application of Information Technologies for Development of Education and Economic Growth». Tashkent, july 3–5, 2003., p. 97–98.











