Аппаратно-ориентированный алгоритм вычисления коэффициентов в базисах J-функций
Авторы: Рахимов Бахтияр Саидович, Жуманиёзов Сардор Пирназарович
Рубрика: 3. Автоматика и вычислительная техника
Опубликовано в
III международная научная конференция «Актуальные вопросы технических наук» (Пермь, апрель 2015)
Дата публикации: 08.04.2015
Статья просмотрена: 57 раз
Библиографическое описание:
Рахимов, Б. С. Аппаратно-ориентированный алгоритм вычисления коэффициентов в базисах J-функций / Б. С. Рахимов, С. П. Жуманиёзов. — Текст : непосредственный // Актуальные вопросы технических наук : материалы III Междунар. науч. конф. (г. Пермь, апрель 2015 г.). — Пермь : Зебра, 2015. — С. 59-62. — URL: https://moluch.ru/conf/tech/archive/125/7721/ (дата обращения: 24.04.2025).
Широкая популярность сплайн — методов объясняется тем, что они служат универсальным инструментом приближения функций и по сравнению с другими математическими методами при равных с ними информационных и аппаратных затратах обеспечивают большую точность вычислений [1, 2, 3, 4].
Любой сплайн Sm (x) степени m дефекта 1, интерполирующий заданную функцию f (x), может быть единственным образом представлен В — сплайнами в виде суммы [1,3,6]:
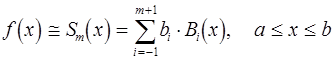 (1)
(1)
где bi — коэффициенты.
Существуют различные способы вычисления коэффициентов [2, 3, 4, 7].
В случае применения параболических В-сплайнов по формуле (1) требуются три базисных слагаемых. Будем считать, что значения аргумента приведены к диапазону [0,1], тогда значение функции вычисляется по формуле:
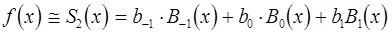 (2)
(2)
Остальные базисные В-сплайны на этом под интервале равны нулю, и следовательно, в образовании суммы они не участвуют.
Одним из важных свойств параболических сплайнов является непрерывность ее производных первого и второго порядка. Это свойство может быть использована для разработки аппаратно-ориентированного алгоритма вычисления коэффициентов в кусочно — квадратических базисах, что позволяет получить высокопроизводительные вычислительные структуры для кусочно полиномиальной обработки сигналов и функций, отличающееся также высокой точностью [2, 4, 5, 6].
Например, первая и вторая производные от параболического базисного сплайна:
1) на отрезке -1,5 £ х < -0,5
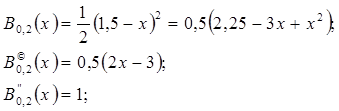
2) на отрезке -0,5 £ х < 0,5
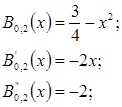
3) на отрезке 0,5 £ х < 1,5
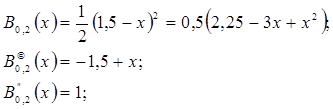
Подставляя значения производных второй степени вместо значений базисных сплайнов, получим формулу:
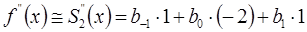 (3)
(3)
Полученный массив представляет собой значения производной второго порядка от исходной функции. Отметим, что формула (3) даёт возможность определить производную второй степени даже если аналитическая форма исходной функции неизвестна. Вычислить значения аппроксимирующего сплайна 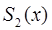 по формуле (3).
по формуле (3).
Таким образом, в результате сочетания хороших дифференциальных свойств базисных сплайнов и возможностей быстрых преобразований Уолша можно предложить следующий алгоритм вычисления коэффициентов в базисах J — функций [3,4,6]:
1. Ввод исходной функциональной зависимости, т. е. ввод массива реальных экспериментальных данных.
2. Определить b-коэффициенты
3. Формировать массив 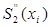
4. Над элементами полученного массива выполнить быстрые преобразования Уолша и определить коэффициенты. Эти коэффициенты уже являются коэффициентами в базисе J — функций.
5. Вывести массив коэффициентов.
На рис 1. приведена блок-схема алгоритма вычисления коэффициентов в базисах J — функций.
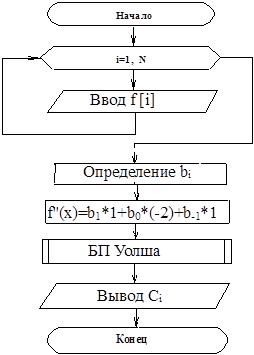
Рис 1. Блок-схема алгоритма вычисления коэффициентов в базисах J-функций
Проведенные численные эксперименты позволяют сделать вывод о том, что число нулевых коэффициентов при обработке массивов геофизических данных, полученных в результате магниторазведки составляет от 5 % до 15 %, а при обработке элементарных функций (а также функций состоящих из их комбинаций) этот показатель составляет от 5 % до 85 %. В табл. 1 приведены результаты численных экспериментов. Были проведены исследования по определению сравнительных характеристик полученных кусочно — квадратических базисов и кусочно-постоянных базисов Уолша. Результаты этого исследования приведены в таблице 1.
Таблица 1
Результаты численных экспериментов
|
№ |
Функция |
КП |
КЛ |
КК |
|
1 |
|
46,8 % |
81,2 % |
85,6 % |
|
2 |
y=Х*Sin X |
5,4 % |
28,1 % |
64,0 % |
|
3 |
y=eX |
29,6 % |
65,6 % |
85,4 % |
|
4 |
y=Ln(1+X) |
33,5 % |
70,3 % |
81,2 % |
|
5 |
y=e-X |
39,8 % |
75,0 % |
82,4 % |
|
6 |
y=Sin 2 |
52,3 % |
59,3 % |
76,5 % |
|
7 |
Данные вибрационных испытаний |
5,6 % |
7,0 % |
14,7 % |
Таким образом, предложенный алгоритм является аппаратно-ориентированным и позволяет применить существующие алгоритмы быстрых преобразований Уолша в базисах ортогональных кусочно-постоянных функций для расчета коэффициентов как кусочно-линейных, так и кусочно-квадратических базисах Уолша.
Литература:
1. Ахмед Н., Рао К. Ортогональные преобразования при обработке цифровых сигналов. -М.: Связь, 1980. — 248 с.
2. Верлань А. Ф., Абдусаттаров Б. Б., Акбаров Ш. А. Алгоритмические и структурные методы повышения быстродействия специализированных устройств при реализации интегральных моделей нелинейных динамических объектов // Электронное моделирование. — 1987. — № 6. — С. 42–44.
3. Касымов С. С., Зайнидинов Х. Н., Рахимов Б. С. Применение базисных сплайнов для предварительной обработки экспериментальных данных // Тезисы докл. XVI — Международная научная конф., Санкт — Петербург, 2003.
4. Ракощиц В. С., Козлов А. В., Можаев И. А. и др. Специализированные микропроцессоры, реализующие быстрые преобразования // Цифровая обработка сигналов: сб. статьей. — М.: Наука, 1981. — С. 206–217.
5. Рахимов Б. С. Применение кусочно — постоянных, кусочно — линейных и кусочно — квадратических базисных функций Уолша для спектральной обработки сигналов. // Тезисы докл. сб. науч. статьей., Ташкент, -С 319–320.
6. Рахимов Б. С. Проектирование спецпроцессов для обработки сигналов на основе матричной диаграммы занятности.// Научно — технический журнал Ферганского политехнического института. 2003, № 4, — С 31–34.
7. Рахимов Б. С. Кусочно — полиномиальные методы на основе функций Уолша.// Актуальные вопросы в области технических и социально-экономических наук. Межвузовский сб. научн. трудов. Ташкент 2006, вып.1., — С. 42–43.







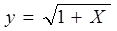
 Х
Х



