Разностно-потенциальные коэффициенты как параметры схемы замещения электрического процесса в ванне многоэлектродных печей
Автор: Ильгачёв Анатолий Николаевич
Рубрика: 4. Электротехника
Опубликовано в
III международная научная конференция «Актуальные вопросы технических наук» (Пермь, апрель 2015)
Дата публикации: 05.04.2015
Статья просмотрена: 46 раз
Библиографическое описание:
Ильгачёв, А. Н. Разностно-потенциальные коэффициенты как параметры схемы замещения электрического процесса в ванне многоэлектродных печей / А. Н. Ильгачёв. — Текст : непосредственный // Актуальные вопросы технических наук : материалы III Междунар. науч. конф. (г. Пермь, апрель 2015 г.). — Пермь : Зебра, 2015. — С. 76-79. — URL: https://moluch.ru/conf/tech/archive/125/7789/ (дата обращения: 03.04.2025).
Работа многих действующих трёхфазных руднотермических печей (РТП) происходит в условиях несимметричности электрического режима печного контура и ванны, которая может наблюдаться как в переходных, так и в стационарных режимах. Несимметричность электрического режима РТП обусловлена действием различных причин геометрического, электрического и технологического характера. Проявление этих факторов обнаруживается в отсутствии равенства действующих значений токов в электродах и мощностей в фазах и участках ванны, в различии значений и знака переносимой мощности с фазы на фазу и, как следствие, в перекосе активных и реактивных мощностей фаз, появлении «дикой» и «мертвой» фаз [1, 2]. При этом наблюдается неодинаковое относительно электродов распределение электрической мощности по объёму ванны, приводящее к неодинаковым условиям протекания электротехнологических процессов вокруг них. Все это ведет к ухудшению энергетических и технологических показателей работы установок.
В значительной части электродных РТП тепло в технологических зонах выделяется в основном за счет протекания тока по нагретым электропроводящим материалам среды ванны. Такие печи являются установками резистивного объемного нагрева. Существующие методы исследования электрических процессов в печном контуре и характеристик электрического поля ванн электродных установок резистивного нагрева не позволяют с необходимой точностью выявлять, учитывать и устранять действия факторов, приводящих к несимметричности электрического режима. Важной задачей повышения энергетической эффективности рассматриваемых установок является разработка методов исследования параметров схем замещения ванн в этих условиях.
При решении задач анализа и синтеза электрических режимов РТП в случае гармонической формы питающих ванну токов токоподвод, электроды, шихтовые, шлаковые материалы и расплав, расположенные в ванне, необходимо рассматривать как единую систему и производить расчёт электромагнитного поля одновременно для всей системы решением квазиволнового уравнения
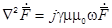 ,
,
где 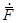 — вектор электрической или магнитной напряжённости поля в комплексной форме; mm0 — магнитная проницаемость среды; g — удельная проводимость среды; w — круговая частота переменного тока.
— вектор электрической или магнитной напряжённости поля в комплексной форме; mm0 — магнитная проницаемость среды; g — удельная проводимость среды; w — круговая частота переменного тока.
При пренебрежении влиянием поверхностного эффекта в шлаке и шихте ванны и предположении однородности удельной электрической проводимости их материалов электрическое поле ванны является потенциальным, квазистационарным, описывается уравнением Лапласа и может быть рассчитано без учета действия магнитного поля.
В настоящее время для характеристики ванны электродных печей резистивного нагрева как приёмника электрической энергии и анализа её взаимодействия с токоподводом и источником питания находят применение две разновидности схем её замещения: 1) в виде звезды входных сопротивлений; 2) в виде полного многоугольника с частичными проводимостями. Достоинство первой схемы замещения состоит в простоте представления и определения характеристик ванны как приёмника электроэнергии. Вместе с тем она обладает недостатком, состоящим в том, что параметры её элементов зависят не только от геометрии ванны, формы, пространственного расположения электродов и электрических свойств расположенных в ней материалов шихты, но и от режима питания, например от соотношения напряжений на электродах,
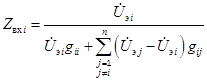 , i = 1, 2, …, n, (1)
, i = 1, 2, …, n, (1)
где gii, gij — частичные проводимости схемы замещения ванны, 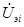 — напряжение на участке «электрод — подина» i-го электрода.
— напряжение на участке «электрод — подина» i-го электрода.
При изменении электрического режима многоэлектродной установки вследствие переключения ступени напряжения печного трансформатора изменяются напряжения на электродах относительно подины, что ведёт в соответствии с (1) к изменению входных сопротивлений ванны, и тем самым создаётся трудность анализа взаимодействия ванны с источником питания с применением входных сопротивлений. Зависимость входных сопротивлений ванны от напряжений на участках «электрод — подина» усиливается с уменьшением расстояния между осями соседних электродов и увеличением площади их поперечного сечения, площади рабочей поверхности электродов. В условиях несимметричности электрического режима входные сопротивления схемы замещения ванны для электрического поля содержат как активные, так и реактивные составляющие.
При ранее принятых допущениях для электрического процесса в ванне частичные проводимости её схемы замещения не зависят от режима питания ванны. Исследование электрического режима многоэлектродных печей с использованием такой схемы замещения ванны связано с составлением и решением системы уравнений, число которых достаточно велико. Поэтому для анализа взаимодействия ванны с источником питания и токоподводом эта схема замещения ванны не получила столь широкого распространения.
Согласно принципу суперпозиции, справедливому для линейных систем, к которым следует отнести при принятых допущениях ванну многоэлектродной печи, напряжение на участке ванны «электрод — подина» можно представить алгебраической суммой частичных напряжений, каждое из которых обусловлено действием тока, протекающим в одном из электродов
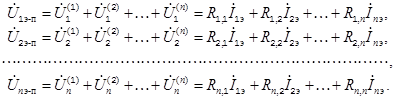
где n — количество электродов; 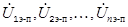 — напряжения на участках ванны «электрод — подина» в комплексной форме,
— напряжения на участках ванны «электрод — подина» в комплексной форме, 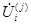 , j = 1, 2, …, n — частичные напряжения на участке ванны «i-й электрод — подина»,
, j = 1, 2, …, n — частичные напряжения на участке ванны «i-й электрод — подина», 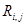 , i, j = 1, 2, …, n — коэффициенты пропорциональности, имеющие размерность сопротивления и названные в [3] разностно-потенциальными коэффициентами (РПК) схемы замещения ванны.
, i, j = 1, 2, …, n — коэффициенты пропорциональности, имеющие размерность сопротивления и названные в [3] разностно-потенциальными коэффициентами (РПК) схемы замещения ванны.
РПК 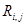 , i, j = 1, …. n определяют связь между частичными напряжениями
, i, j = 1, …. n определяют связь между частичными напряжениями 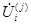 на участках ванны «электрод-подина» и токами электродов печи
на участках ванны «электрод-подина» и токами электродов печи 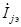 , j = 1, …. n. При принятых выше допущениях они зависят от формы и геометрических размеров ванны, формы рабочих поверхностей, размеров, взаимного расположения и заглублений электродов, а также от электрической проводимости материалов среды ванны [4]. В зависимости от того к каким электродам относятся частичное напряжение
, j = 1, …. n. При принятых выше допущениях они зависят от формы и геометрических размеров ванны, формы рабочих поверхностей, размеров, взаимного расположения и заглублений электродов, а также от электрической проводимости материалов среды ванны [4]. В зависимости от того к каким электродам относятся частичное напряжение 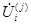 на участке ванны и ток электрода
на участке ванны и ток электрода 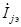 , различают собственные и взаимные РПК. Например, собственный РПК
, различают собственные и взаимные РПК. Например, собственный РПК 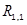 ванны электродной печи определяет связь между частичным напряжением
ванны электродной печи определяет связь между частичным напряжением 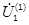 участка ванны «первый электрод — подина», наводимым током первого электрода за счет его растекания по материалам среды ванны, и значением тока этого электрода. В свою очередь, взаимный РПК
участка ванны «первый электрод — подина», наводимым током первого электрода за счет его растекания по материалам среды ванны, и значением тока этого электрода. В свою очередь, взаимный РПК 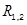 устанавливает связь между частичным напряжением
устанавливает связь между частичным напряжением 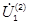 участка ванны «первый электрод — подина» и током, протекающим во втором электроде.
участка ванны «первый электрод — подина» и током, протекающим во втором электроде.
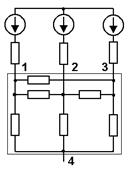
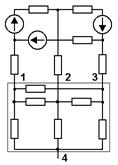
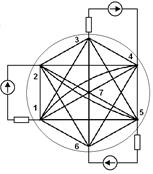
Предлагается символически обозначать РПК схемы замещения ванны, используя известные графические элементы для изображения резисторов и взаимных индуктивных сопротивлений. Например, для печи с тремя электродами схема замещения ванны с РПК будет выглядеть так, как показано на рис 1.
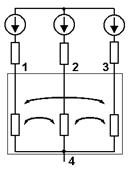
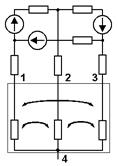
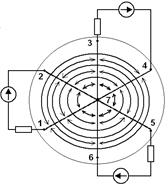
С использованием физической (водяной) модели электрических процессов в ванне печи и опытов холостого хода ванны (рис. 2) можно определить РПК схемы замещения ванны [4].
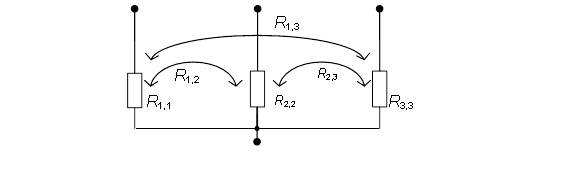
Рис. 1. Схема замещения ванны с использованием РПК трехэлектродной печи
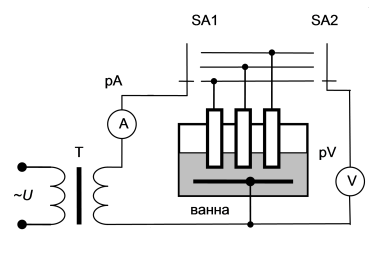
Рис. 2. Электрическая схема физической модели ванны трёхэлектродной печи для определения РПК схемы замещения
Сущность опыта холостого хода ванны модели состоит в том, что её питание осуществляется путём подключения вывода источника питания к одному из электродов, а другой его вывод подключается к подовому электроду. Оставшиеся электроды оставляют не подключенными к электрической цепи источника питания модели. В процессе моделирования фиксируется пространственное положение электродов в ванне и к каждому из них поочередно с помощью переключателя SA1 подключается вывод вторичной обмотки трансформатора T, второй вывод которого постоянно подсоединён к металлической пластине, расположенной на дне ванны. С помощью амперметра pA измеряются ток, протекающий в электроде. Переключатель SA2 коммутирует электрод и вольтметр pV, посредством которого измеряют напряжения на участках «электрод — подина». По результатам измерения определяют РПК схемы замещения ванны:
- собственные РПК — 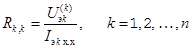 ;
;
- взаимные РПК — 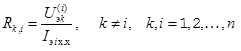 .
.
В таблице приведены данные о количестве ветвей Nв, узлов Nу и контуров Nк электрических цепей с частичными проводимостями, входными сопротивлениями или РПК схем замещения ванн РТП, рассчитанные для некоторых многоэлектродных электрических печей.
Сравнение параметров электрических цепей многоэлектродных печей для различных схем замещения ванн
|
n |
С частичными проводимостями |
С входными сопротивлениями или разностно-потенциальными коэффициентами |
|
||||||
|
Схема |
Nв |
Nу |
Nк |
Схема |
Nв |
Nу |
Nк |
||
|
3 |
|
9 |
5 |
5 |
|
3 |
2 |
2 |
|
|
3 |
|
12 |
7 |
6 |
|
6 |
4 |
3 |
|
|
6 |
|
24 |
7 |
18 |
|
3 |
1 |
3 |
|
Эти данные показывают, что применение РПК в качестве элементов схемы замещения ванны позволяет значительно уменьшить число узлов, ветвей и контуров электрической цепи печи по сравнению с использованием частичных проводимостей при сохранении преимущества перед входными сопротивлениями ванны — независимости параметров элементов схемы замещения от электрического режима. Это преимущество усиливается с увеличением числа электродов печи.
Литература:
1. Струнский Б. М. Расчеты руднотермических печей. М.: Металлургия. 1982.
2. Данцис Я. Б. Методы электротехнических расчетов мощных электропечей. Л.: Энергоиздат, Ленингр. отд-ние. 1982. 232 с.
3. Ильгачёв А. Н. Разностно-потенциальные коэффициенты ванн многоэлектродных печей резистивного нагрева / А. Н. Ильгачёв // Вестник Чувашского университета. 2006. № 2. С. 227–235.
4. Ильгачёв А. Н. Исследование разностно-потенциальных коэффициентов ванн многоэлектродных печей резистивного нагрева // Региональная энергетика и электротехника: проблемы и решения: сб. науч. тр. Вып. 7. Чебоксары: Изд-во Чуваш. ун-та, 2011. С. 196–209.