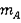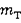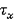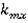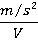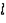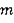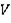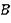Исследование динамики машин
Автор: Эрдэнэ-Очир Мял Уулд
Рубрика: 14. Общие вопросы технических наук
Опубликовано в
III международная научная конференция «Актуальные вопросы технических наук» (Пермь, апрель 2015)
Дата публикации: 07.04.2015
Статья просмотрена: 109 раз
Библиографическое описание:
Эрдэнэ-Очир, Мял Уулд. Исследование динамики машин / Мял Уулд Эрдэнэ-Очир. — Текст : непосредственный // Актуальные вопросы технических наук : материалы III Междунар. науч. конф. (г. Пермь, апрель 2015 г.). — Пермь : Зебра, 2015. — С. 174-177. — URL: https://moluch.ru/conf/tech/archive/125/7832/ (дата обращения: 19.12.2024).
Введение
Одна из возможностей увеличить производительность грузового крана – это уменьшение движения качения груза при транспортировке. Уменьшение качения груза влияет и на качество штабеловки.
1. Метод и методика
Мы создали математическую модель движения качения груза, используя уравнение Лагранжа второго рода.
Для контроля модели мы использовали готовое уравнение [4]:
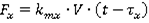
Для разработки уравнения использовали матлав.
2. Математическая модель
На рисунке 1 показана наша расчетная схема крана.
Наша система имеет две степени свободы. Выберем в качестве обобщенных координат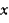 
- координаты тележки и угол 
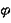, характеризующий отклонение троса, скрепленного с грузом 
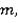от вертикали.
Связь идеальная голономная. Активные силы: силы тяжести, действующие на груз и тележку, сила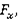 
движущая тележку.
Потенциальная энергия тележки равна нулю: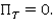 
Координаты груза и тележки:
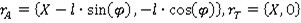
Вычисляем проекции скорости
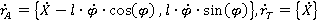
Кинетическая энергия системы
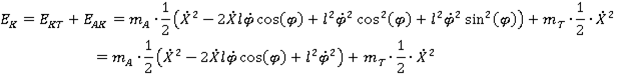
Потенциальная энергия системы
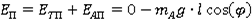
Функция Лагранжа
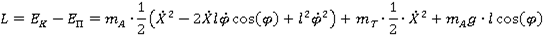
Выполним операции дифференцирования, необходимые для составления уравнений Лагранжа
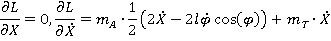
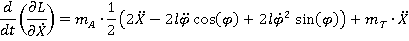
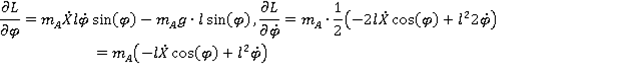
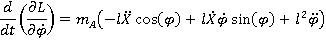
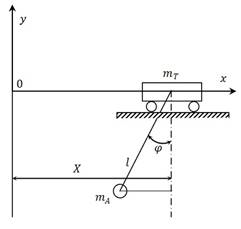
Рис 1. Расчетная схема
Уравнения Лагранжа системы имеют вид
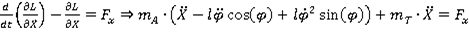(1)
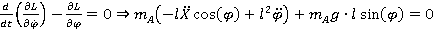(2)
Если (2) делить на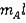 
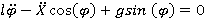(3)
Сила 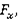движущая тележку: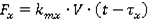 
Таблица 1
Параметры системы
|
Параметры |
Обозначение |
Разметность |
Значение |
|
Масса груза |
|
кг |
0.32 |
|
Масса тележки |
|
кг |
0.7 |
|
Константа времени |
|
с |
0.024 |
|
Время |
t |
c |
3 |
|
Коэффициент ускорения |
|
|
5.8808 |
|
Длина троса |
|
|
1 |
|
Напряжение двигателя |
|
|
20 |
Ограничимся рассмотрением малых колебаний качения груза, поэтому в полученных уравнениях сохраним лишь линейные слагаемые:
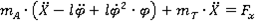
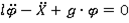
Запишем уравнения движения в виде:
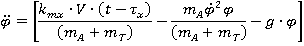
Мы решим уравнения, используя программу Matlab.
Преобразуем уравнение в уравнение 1-ого порядка. Обозначим:
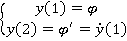
Зададим начальные условия
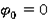
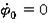
Уравнение имеет вид
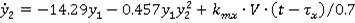
На рисунке 2 показан m-файл для разработки движения.
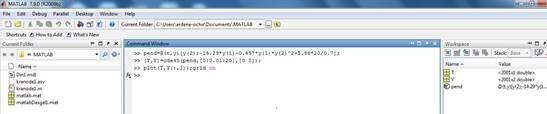
Рис 2. m-файл
На рисунке 3 показан получившийся график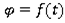
без контроля.
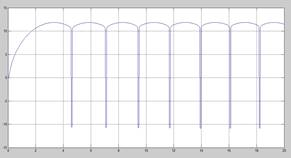
Рис 3. 
На рисунке 4 – график, использующий контрольную функцию.
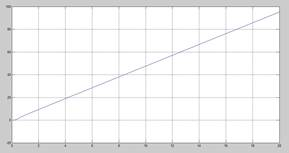
Рис 4. с контрольной функцией
Вывод: Используя контрольную функцию, уменьшили качение груза.
Литература:
1. Oleg Vinogradob. Fundamentals of kinematics and dynamics of machines and mechanisms. CRC Press. 2000.
2. Мещерский И. В. Задачи по теоретической механике. Изд-во “Лань”, 1998. -448 с.
3. Л. А. Мироновский, К. Ю. Петрова. Введение в матлав. Санкт-Петербург. 2005 г.
4. FAISAL ALTAF. Modeling and Event-Triggered Control of Multiple 3D Tower Cranes over WSNs. Stockholm, Sweden October 2010
