Применение системы уравнений Юла — Уолкера для имитации изотропных случайных полей
Авторы: Андриянов Никита Андреевич, Дементьев Виталий Евгеньевич
Рубрика: 1. Информатика и кибернетика
Опубликовано в
IV международная научная конференция «Современные тенденции технических наук» (Казань, октябрь 2015)
Дата публикации: 04.10.2015
Статья просмотрена: 1657 раз
Библиографическое описание:
Андриянов, Н. А. Применение системы уравнений Юла — Уолкера для имитации изотропных случайных полей / Н. А. Андриянов, В. Е. Дементьев. — Текст : непосредственный // Современные тенденции технических наук : материалы IV Междунар. науч. конф. (г. Казань, октябрь 2015 г.). — Казань : Бук, 2015. — С. 2-6. — URL: https://moluch.ru/conf/tech/archive/163/8920/ (дата обращения: 24.04.2025).
Рассмотрена возможность использования двумерных систем уравнений Юла — Уолкера для расчета коэффициентов корреляции по заданной корреляционной функции. Выполнено сравнение для трехточечных и восьмиточечных моделей.
Ключевые слова: модели изображений, оценивание параметров, уравнения Юла — Уолкера
Широкое распространение различных систем регистрации земной поверхности обеспечивает человека огромным количеством информации и, вместе с тем, требует разработки качественно новых алгоритмов обработки получаемых данных. Такими данными, в частности, являются данные дистанционного зондирования Земли из космоса. Вообще говоря, спутниковые снимки могут быть описаны в четырехмерном пространстве: первая координата и вторая координата — собственно пространственные координаты; третья — время, т. е. имеются последовательности изображений; четвертая — номер спектрального диапазона, т. к. съемка происходит в различных частотных диапазонах. В связи с этим желательно, чтобы разрабатываемые алгоритмы вместе с высокой эффективностью работы сочетали бы в себе и быстродействие. Возникает задача цифровой обработки многомерных сигналов [1].
Вместе с тем, на начальном этапе исследования подобных многомерных массивов данных допустимо упрощение, заключающееся в переходе к двумерным сигналам. Действительно, зачастую предлагаются модели изображений, в которых функция яркости является функцией двух переменных: пространственных координат по осям X и Y соответственно. В их числе авторегрессионные модели [2,3]. Основным преимуществом таких моделей является удобное математическое описание, что позволяет достаточно быстро исследовать их свойства. Тем не менее, для описания пространственно-неоднородного материала авторегрессионные модели являются малоприменимыми. Решение этой проблемы может быть получено с переходом к дважды стохастическим моделям изображений [4–6]. С помощью авторегрессионных моделей достаточно хорошо описываются анизотропные случайные поля (СП), однако их использование для описания изотропных СП вызывает трудности.
Таким образом, цель данной работы — определение таких параметров авторегрессионных моделей, которые бы позволяли получить СП, близкие по характеристикам к изотропным. При этом предлагается использовать системы уравнений Юла — Уолкера, т. к. с их помощью по заданной корреляционной функции (КФ) могут быть найдены коэффициенты корреляции.
В начале рассмотрим, например, модель Хабиби
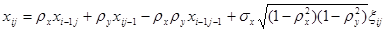 , (1)
, (1)
где 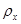 и
и 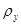 — корреляционные параметры по строке и столбцу;
— корреляционные параметры по строке и столбцу; 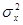 — дисперсия формируемой модели;
— дисперсия формируемой модели; 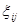 — случайная величина, математическое ожидание которой равно нулю, а дисперсия — единице.
— случайная величина, математическое ожидание которой равно нулю, а дисперсия — единице.
Запишем ковариационную функцию модели (1)
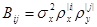 . (2)
. (2)
Анализ выражения (2) показывает, что имитируемое СП является анизотропным, а оценка корреляционных параметров может быть успешно произведена по отдельным осям.
Для описания изотропного СП будем исходить из предположения о том, что модель состоит из нескольких точек. Соответственно, сколько точек, столько и коэффициентов корреляции. Представим модель в виде
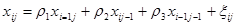 . (3)
. (3)
Здесь коэффициенты 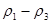 уже не представляют собой корреляционные параметры по строке и по столбцу, а дисперсия случайной величины
уже не представляют собой корреляционные параметры по строке и по столбцу, а дисперсия случайной величины 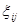 зависит от значений коэффициентов
зависит от значений коэффициентов 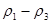 .
.
Для полной реализации модели (3) необходимо несколько начальных условий. Получим их из значений ковариационной функции изотропного СП
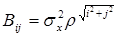 . (4)
. (4)
Или, выполняя нормировку выражения (4), запишем его как
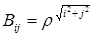 .
.
Далее необходимо построить и решить систему уравнений Юла — Уолкера [7]. При этом необходимо обобщить ее одномерную запись на двумерный случай.
Пусть имеется модель
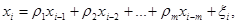
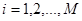 , (5)
, (5)
где m — порядок авторегрессии, 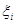 — случайная величина с гауссовым распределением,
— случайная величина с гауссовым распределением, 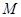 — длина последовательности.
— длина последовательности.
С помощью подбора коэффициентов 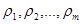 можно получить гауссовские случайные последовательности
можно получить гауссовские случайные последовательности 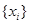 ,
, 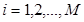 , с разнообразными корреляционными свойствами. Показано [7], что для значений КФ можно использовать соотношение:
, с разнообразными корреляционными свойствами. Показано [7], что для значений КФ можно использовать соотношение:
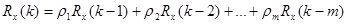 ,
, 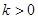 (6)
(6)
Подстановка в (6) значений k = 1, 2, …, m дает известную систему уравнений Юла — Уолкера, которая, например, для систем второго порядка примет вид:
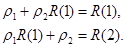
Решение этой системы позволяет найти коэффициенты 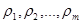 уравнения авторегрессии (5) по, заданным заранее или оцененным на основе эксперимента, значениям Rx(1), Rx(2), …, Rx(m) корреляционной функции случайного процесса.
уравнения авторегрессии (5) по, заданным заранее или оцененным на основе эксперимента, значениям Rx(1), Rx(2), …, Rx(m) корреляционной функции случайного процесса.
Аналогичную связь корреляционных параметров и значений КФ легко записать также для двумерного процесса или изображения.
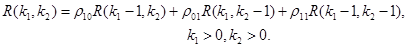
Для увеличения числа коэффициентов запишем модель в следующем виде
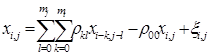 ,
, 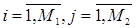 ,
,
где 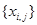 — реализация СП (изображения);
— реализация СП (изображения); 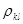 - коэффициенты корреляции для элементов, отстающих друг от друга по осям i и j на k и l пикселей соответственно;
- коэффициенты корреляции для элементов, отстающих друг от друга по осям i и j на k и l пикселей соответственно; 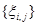 — двумерная случайная последовательность независимых гауссовских случайных величин с нулевым средним
— двумерная случайная последовательность независимых гауссовских случайных величин с нулевым средним 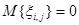 и дисперсией
и дисперсией 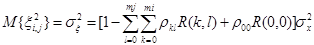 ; mi и mj — порядки авторегрессий; M1 и M2 — размеры изображения.
; mi и mj — порядки авторегрессий; M1 и M2 — размеры изображения.
Тогда выражение для расчета значений КФ
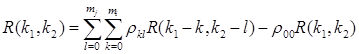 ,
, 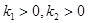 .
.
С помощью статистического моделирования в Matlab сравним результаты для трехточечной и восьмиточечной моделей. При этом КФ изотропного СП рассчитаем для коэффициента 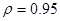 . Начальные условия в этом случае
. Начальные условия в этом случае
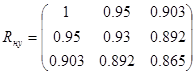 .
.
Тогда, решая систему уравнений, находим вектора коэффициентов корреляции
- 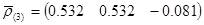 — для трехточечной модели;
— для трехточечной модели;
- 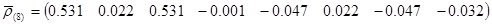 для восьмиточечной модели.
для восьмиточечной модели.
Используя полученные коэффициенты, выполним реализацию модели (размер 200x200). Затем по полученной модели рассчитаем ее ковариационную функцию. Будем сравнивать значения экспериментальной ковариационной функции со значениями теоретической функции изотропного СП. Результаты имитации представлены в таблице 1 (трехточечная модель) и таблице 2 (восьмиточечная модель)
Таблица 1
Сравнительная характеристика КФ трехточечной модели и изотропного СП
|
КФ трехточечной модели |
КФ изотропного СП |
||||||||||
|
i j |
1 |
2 |
3 |
4 |
5 |
i j |
1 |
2 |
3 |
4 |
5 |
|
1 |
0.930 |
0.687 |
0.467 |
0.303 |
0.190 |
1 |
0.930 |
0.892 |
0.850 |
0.809 |
0.770 |
|
2 |
0.687 |
0.655 |
0.542 |
0.411 |
0.296 |
2 |
0.892 |
0.865 |
0.831 |
0.795 |
0.759 |
|
3 |
0.467 |
0.542 |
0.523 |
0.453 |
0.365 |
3 |
0.850 |
0.831 |
0.804 |
0.774 |
0.741 |
|
4 |
0.303 |
0.411 |
0.453 |
0.440 |
0.392 |
4 |
0.809 |
0.795 |
0.774 |
0.748 |
0.720 |
|
5 |
0.190 |
0.296 |
0.365 |
0.392 |
0.381 |
5 |
0.770 |
0.759 |
0.741 |
0.720 |
0.696 |
Таблица 2
Сравнительная характеристика КФ восьмиточечной модели и изотропного СП
|
КФ восьмиточечной модели |
КФ изотропного СП |
||||||||||
|
i j |
1 |
2 |
3 |
4 |
5 |
i j |
1 |
2 |
3 |
4 |
5 |
|
1 |
0.930 |
0.892 |
0.713 |
0.507 |
0.347 |
1 |
0.930 |
0.892 |
0.850 |
0.809 |
0.770 |
|
2 |
0.892 |
0.865 |
0.751 |
0.598 |
0.459 |
2 |
0.892 |
0.865 |
0.831 |
0.795 |
0.759 |
|
3 |
0.713 |
0.751 |
0.714 |
0.621 |
0.514 |
3 |
0.850 |
0.831 |
0.804 |
0.774 |
0.741 |
|
4 |
0.507 |
0.598 |
0.621 |
0.586 |
0.521 |
4 |
0.809 |
0.795 |
0.774 |
0.748 |
0.720 |
|
5 |
0.347 |
0.459 |
0.514 |
0.521 |
0.494 |
5 |
0.770 |
0.759 |
0.741 |
0.720 |
0.696 |
Анализ полученных результатов позволяет сделать следующие выводы:
- применение уравнений Юла — Уолкера для двумерного случая позволяет получить СП с корреляционными свойствами, близкими по форме к свойствам изотропных СП;
- убывание статистической связи в таких моделях по строке и по столбцу в целом происходит быстрее, чем по диагонали;
- точность, полученных в результате имитации, моделей увеличивается при переходе от трехточечной модели к восьмиточечной. Дисперсии ошибки результатов таблицы 1 и таблицы 2: 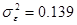 и
и 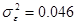 соответственно.
соответственно.
На рис. 1 представлены, полученные при моделировании, изображения.


а б
Рис. 1 Моделирование свойств изотропных СП с помощью трехточечной (а) и восьмиточечной (б) моделей
Таким образом, предложен способ формирования изотропных СП на основе авторегрессионных моделей с коэффициентами, рассчитанными из уравнений Юла — Уолкера. При этом, чем больше коэффициентов в модели, тем точнее будет приближение к заданной КФ.
Литература:
1. Даджион Д., Мерсеро Р. Цифровая обработка многомерных сигналов. — М.: Мир, 1988, 488 с.
2. Васильев К. К., Ташлинский А. Г., Крашенинников В. Р., Статистический анализ последовательностей многомерных изображений // Наукоемкие технологии, 2013, № 5, с. 5–11
3. Васильев К. К., Дементьев В. Е. Авторегрессионные модели многомерных изображений // Наукоемкие технологии, 2013, т. 14, № 15, с. 12–15
4. Васильев К. К., Дементьев В. Е., Андриянов Н. А. Оценивание параметров дважды стохастических случайных полей // Радиотехника. — 2014. — № 7, с. 103–106
5. Андриянов Н. А., Дементьев В. Е. Формирование временных последовательностей дважды стохастических моделей изображений // Современные проблемы проектирования, производства и эксплуатации радиотехнических систем: Сборник научных трудов девятой Всероссийской научно-практической конференции (с участием стран СНГ), г. Ульяновск, 1–2 октября 2015 г. — Ульяновск, УлГТУ, 2015. — с. 89–93.
6. Андриянов Н. А. Идентификация параметров дважды стохастических авторегрессионных моделей случайных процессов / Н. А. Андриянов, К. К. Васильев, В. Е. Дементьев // 16-я Международная конференция “Цифровая обработка сигналов и ее применение — DSPA-2014”, Москва, Россия. Доклады, 2014. Т. 1. c. 109 -113.
7. Васильев К. К. Методы обработки сигналов: учебное пособие / К. К. Васильев. — Ульяновск, 2001. — 80 с.
Ключевые слова
оценивание параметров, модели изображений, уравнения Юла — УолкераПохожие статьи
Описание нестационарных случайных процессов с помощью модели с переменными параметрами
В настоящей статье представлен алгоритм моделирования неоднородных случайных процессов, основанный на применении моделей с изменяющимися параметрами. При этом внимание уделяется моделям на основе базового набора возможных значений корреляционных пара...
Программное обеспечение и математическая реализация фрактального распознавания искусственных и природных объектов
Использование фрактальных сигнатур для задач обнаружения и идентификации различных целей является основой перспективных методов. Предложен адаптивный алгоритм для фрактального распознавания искусственных объектов, основанный на концепции сглаживания ...
Математическая модель распространения электромагнитных волн на границе раздела «лед — вода»
Разработана математическая модель распространения сферических электромагнитных волн внутри слоя льда. В основе модели лежат направленные функции Грина с неоднородными по углу граничными условиями. Такая модель позволяет представить неоднородную повер...
Сравнение точности методов численного интегрирования на примере элементарных функций
В статье авторы проводят вычислительный эксперимент, посредством которого производится сравнение возможностей различных методов численного интегрирования на примере элементарной функции.
Анализ методов решения уравнения Баклея — Леверетта
В статье выполнено сравнение методов Лакса-Вендрофа, Лакса-Фридрихса и Противопоточного метода решения уравнения Баклея-Леверетта.
О численных методах решения эволюционных уравнений на примере математической модели «хищник-жертва»
Поставлена математическая задача о двух взаимодействующих на отрезке популяциях по принципу хищник-жертва. Математическая модель представляет собой краевую задачу для системы двух нелинейных уравнений в частных производных. Исследуется устойчивость с...
Вероятностная оценка ковариационной матрицы для фильтра Кальмана при полярных системах координат
При измерении позиции объекта радаром возникает вопрос о точности измерения. Чтобы минимизировать ошибку измерения используется Фильтр Калмана. Для этого необходимо чтобы измерение было бы выполнено в Декартовых системах координат, но большинство рад...
Математическая модель конкуренции двух популяций на линейном ареале
Поставлена математическая задача о конкуренции на линейном ареале двух популяций. Математическая модель представляет собой краевую задачу для системы двух нелинейных дифференциальных уравнений в частных производных. Исследуется устойчивость стационар...
Математическая модель синтеза антенной решетки из пяти точечных источников в свободном пространстве
Разработана математическая модель синтеза антенных решеток из пяти точечных излучателей. В основе модели лежат направленные функции Грина, удовлетворяющие граничным условиям неразрывности по угловым координатам. С помощью предложенной модели проведен...
О математических моделях симбиоза
Дается краткий анализ трех моделей симбиоза двух популяций, представленных задачами Коши для обыкновенных дифференциальных уравнений. Математическая модель симбиоза двух популяций на отрезке представлена краевой задачей для системы двух нелинейных ур...
Похожие статьи
Описание нестационарных случайных процессов с помощью модели с переменными параметрами
В настоящей статье представлен алгоритм моделирования неоднородных случайных процессов, основанный на применении моделей с изменяющимися параметрами. При этом внимание уделяется моделям на основе базового набора возможных значений корреляционных пара...
Программное обеспечение и математическая реализация фрактального распознавания искусственных и природных объектов
Использование фрактальных сигнатур для задач обнаружения и идентификации различных целей является основой перспективных методов. Предложен адаптивный алгоритм для фрактального распознавания искусственных объектов, основанный на концепции сглаживания ...
Математическая модель распространения электромагнитных волн на границе раздела «лед — вода»
Разработана математическая модель распространения сферических электромагнитных волн внутри слоя льда. В основе модели лежат направленные функции Грина с неоднородными по углу граничными условиями. Такая модель позволяет представить неоднородную повер...
Сравнение точности методов численного интегрирования на примере элементарных функций
В статье авторы проводят вычислительный эксперимент, посредством которого производится сравнение возможностей различных методов численного интегрирования на примере элементарной функции.
Анализ методов решения уравнения Баклея — Леверетта
В статье выполнено сравнение методов Лакса-Вендрофа, Лакса-Фридрихса и Противопоточного метода решения уравнения Баклея-Леверетта.
О численных методах решения эволюционных уравнений на примере математической модели «хищник-жертва»
Поставлена математическая задача о двух взаимодействующих на отрезке популяциях по принципу хищник-жертва. Математическая модель представляет собой краевую задачу для системы двух нелинейных уравнений в частных производных. Исследуется устойчивость с...
Вероятностная оценка ковариационной матрицы для фильтра Кальмана при полярных системах координат
При измерении позиции объекта радаром возникает вопрос о точности измерения. Чтобы минимизировать ошибку измерения используется Фильтр Калмана. Для этого необходимо чтобы измерение было бы выполнено в Декартовых системах координат, но большинство рад...
Математическая модель конкуренции двух популяций на линейном ареале
Поставлена математическая задача о конкуренции на линейном ареале двух популяций. Математическая модель представляет собой краевую задачу для системы двух нелинейных дифференциальных уравнений в частных производных. Исследуется устойчивость стационар...
Математическая модель синтеза антенной решетки из пяти точечных источников в свободном пространстве
Разработана математическая модель синтеза антенных решеток из пяти точечных излучателей. В основе модели лежат направленные функции Грина, удовлетворяющие граничным условиям неразрывности по угловым координатам. С помощью предложенной модели проведен...
О математических моделях симбиоза
Дается краткий анализ трех моделей симбиоза двух популяций, представленных задачами Коши для обыкновенных дифференциальных уравнений. Математическая модель симбиоза двух популяций на отрезке представлена краевой задачей для системы двух нелинейных ур...











