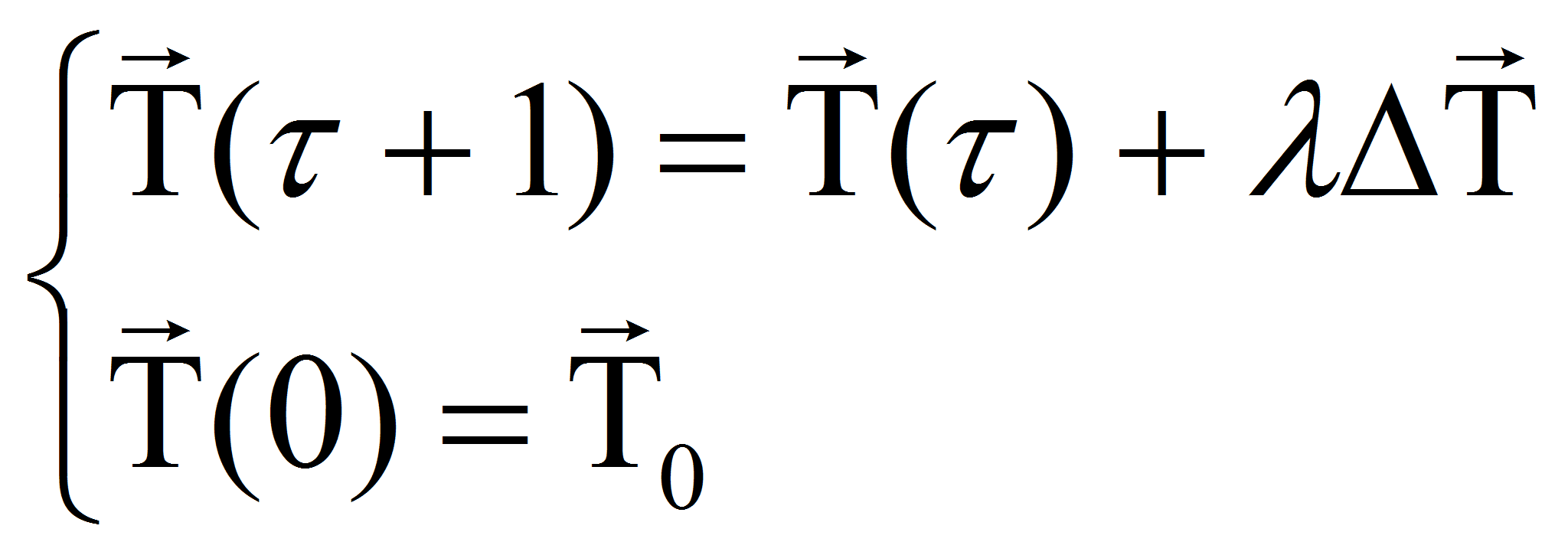Итерационная процедура высокоточного совмещения аффинно-преобразованных изображений

Известные [1-2] точные методы совмещения изображений, основанные чаще всего на вычислении взаимно корреляционных функций анализируемых изображений, обладают большой вычислительной сложностью и, вследствие этого, мало приспособлены для реализации в реальном времени, особенно при идентификации параметров сложного, «аффинного», движения.

В работе для получения высокоточных оценок параметров геометрического рассогласования положения (взаимного смещения) аффинно-преобразованных изображений предложен компенсационный вариант метода функционализации [3]. Метод является обобщением известного градиентного метода вычисления «оптического потока» [4] и основан на использовании соотношения (ФС - уравнения), функционально связывающего параметры движения наблюдаемого объекта с изменениями измеримых характеристик изображения. Под измеримыми понимаются характеристики изображения, значения которых определены на подобластях изображения ненулевой меры. Здесь этот метод используется для определения параметров движения изображения, обладающего тремя степенями свободы (аффинно-преобразованного изображения без растяжения).

Постановка задачи

На анализируемом изображении, заданном равномерно ограниченной и дифференцируемой почти всюду по всем своим аргументам функцией распределения освещенности изображения яркостного объекта ( - вектор смещения в системе координат плоскости изображения, Т – операция транспонирования матрицы), выделяются подобласти – последовательные во времени кадры и ( - начальный момент времени, - кадровый период). Причем является результатом преобразования :

, (1)

- оператор вращения [4], - перенос.

При этом в каждом кадре рассматриваются изображения и соответственно.

Задачей является нахождение оператора , обратного для оператора .

Итерационная процедура определения параметров рассогласования положения изображений

В компенсационном варианте метода функционализации [5-6] для совмещения изображений используют итерационную процедуру, которая заключается в следующем. На каждой итерации (,) кадр трансформируется в кадр с помощью оператора, являющегося оценкой оператора на шаге .

П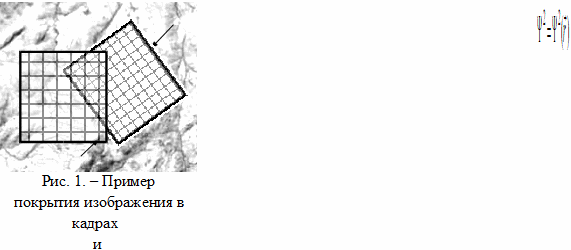о изображениям, покрываемым кадрами и методом функционализации уточняют оценку обратного оператора .

При этом каждый кадр изображения покрывают идентичной системой окон анализа ( – номер окна анализа, - номер кадра) (рис. 1) и для каждой одноименной пары окон , формируют уравнения функциональной связи вида [5]:

, (2)

где 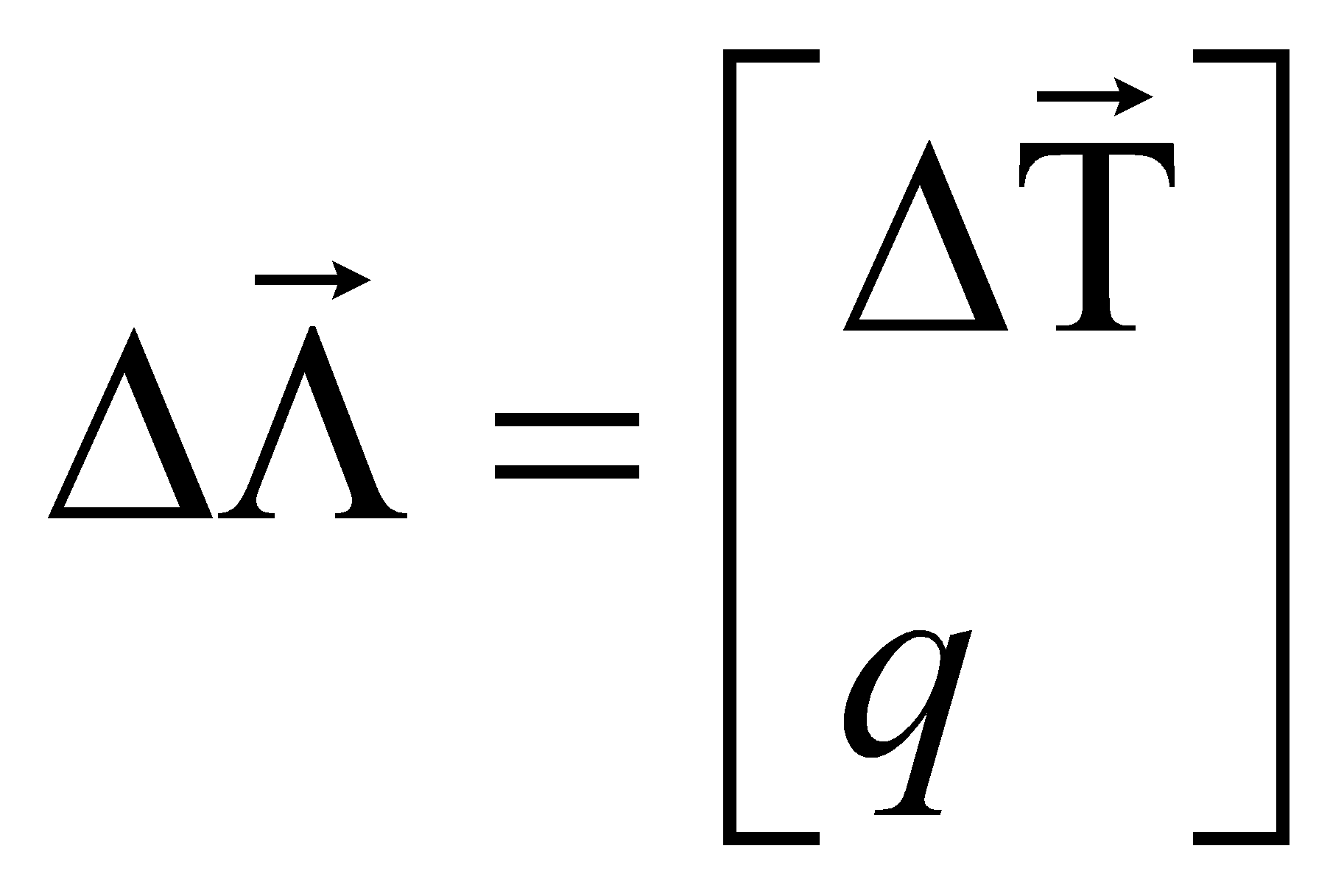- вектор-столбец, - вектор смещения, q –переменная характеризующая изменение освещенности сцены [6];

, - функционал вида:

, (3)

- непрерывная и дифференцируемая почти всюду по всем своим аргументам функция веса;

– матрица коэффициентов, элементы которой определяют из выражений:

;

;

;

;

;

– число ФС-уравнений.

Система (2) в общем случае является переопределенной. Она дает оценки составляющих вектора смещения изображения . Система решается методом квазиобращения [5]. Итерационную процедуру

, (4)

где 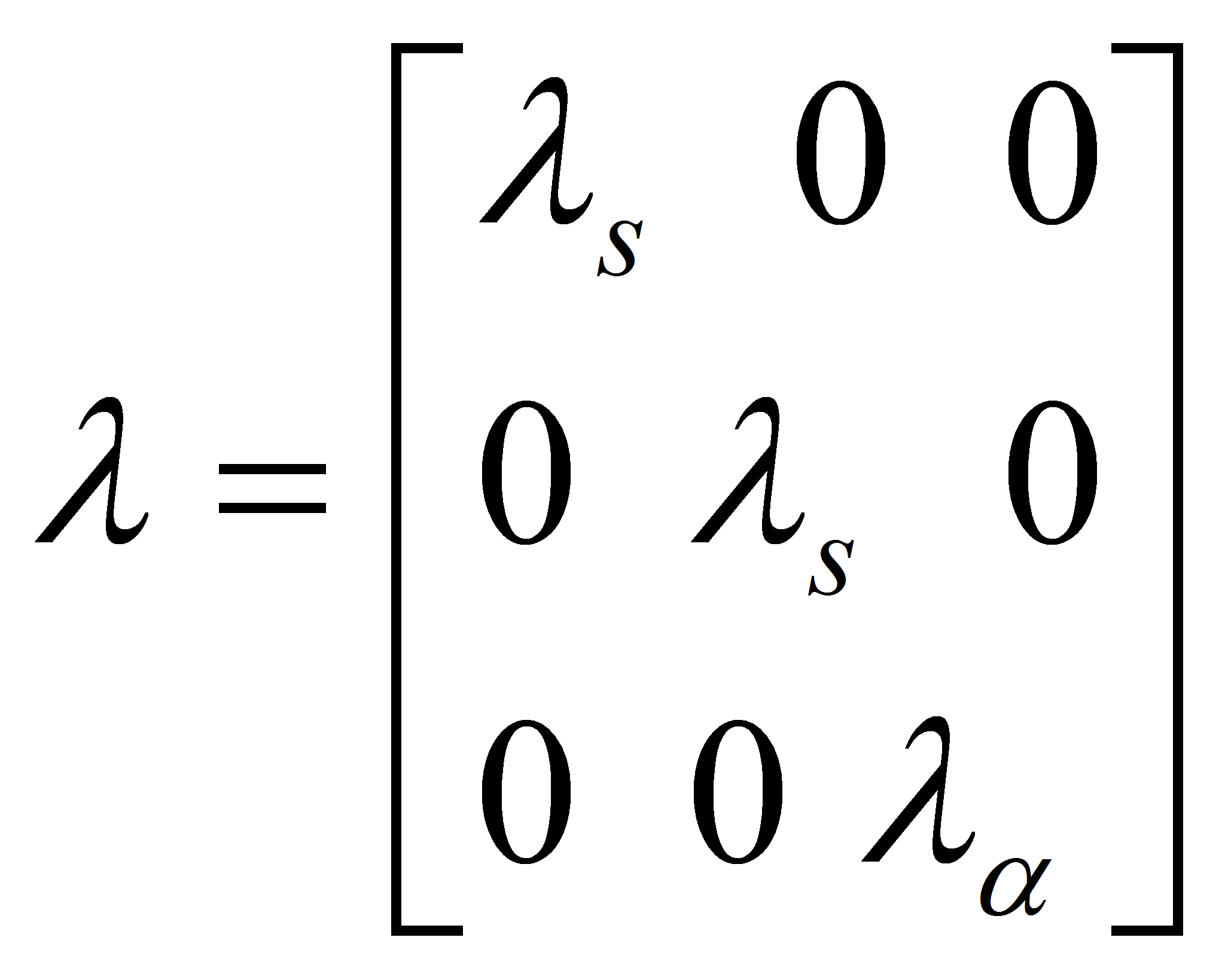– матрица «коэффициентов обратной связи»; – предполагаемая оценка смещения изображения кадра относительно кадра , повторяют до тех пор, пока компоненты вектора смещения на n - ом шаге не станут меньше заданных величин , и .

Приведенный алгоритм требует настройки параметров и размеров окон анализа по условиям сходимости процедуры.

В [6] дана аналитическая оценка сходимости итерационного метода на примере тестового моночастотного изображения вида

(5)

отдельно для плоско-параллельного движения () и вращения в плоскости движения изображения.

Достаточным условием сходимости итерационной процедуры для случая плоско-параллельного движения является выполнение следующих условий, накладываемых на начальное рассогласование положения (перенос) объекта в анализируемых кадрах и значение коэффициента в (4):

. (6)

Таким образом, процесс сходится, если начальное рассогласование кадров и не превышает трети периода тестового изображения.

Условием сходимости итерационного процесса для случая чистого вращения при изменении угла поворота в пределах является:

(7)

где – приращение оценки угла поворота на итерации с номером .

Обозначим через максимальное (критическое) значение, отвечающее достаточному признаку сходимости (7). Считаем, что окна анализа имеют форму квадрата.

В таблице 1 приведена аналитическая оценка зависимости количества итераций итерационного процесса (4) от частоты тестового сигнала при критическом значении коэффициента обратной связи . Условие (7) является лишь достаточным.

Таблица 1

Нетрудно показать, что значение может быть увеличено, при этом скорость сходимости увеличивается.

Результаты исследования влияния на процесс сходимости итерационной процедуры (7) для тестового изображения вида (5) представлены в таблице 2.

При увеличении сначала увеличивается количество итераций, а затем процесс (5) теряет устойчивость. Таким образом, можно сделать вывод, что наилучшая сходимость с точки зрения максимального быстродействия итерационного процесса достигается при . В таблице 2 приведены результаты, соответствующие допустимой погрешности . При других значениях значение остается в тех же пределах.

Таблица 2

Заключение

В статье предложен компенсационный метод определения параметров движения изображений, основанный на итерационной процедуре совмещения изображений. Получены аналитические оценки сходимости и быстродействия метода для аффинного движения изображения, позволяющие существенно расширить область сходимости по начальным данным и уменьшить количество итераций итерационного процесса.

Литература:

1. Fleet David J., Jepson Allan D. Computation of component image velocity from local phase information. //Int. J. Comput. Vision. 1990. - 5. N1.- pp. 77-104.

2. Miike Hidetoshi, Nomura Atsushi, Koga Kazutoshi. Determining image flow from multiple frames based on the continuity equation. //Technol. Repts Yamaguchi Univ. - 1991. - 4. № 5. - P. 387-397.

3. Кузнецов П.К., Семавин В.И. Метод определения параметров движения яркостного поля//Известия ВУЗов. Приборостроение. – 1990. - №6. - С. 26 – 30.

4. Black M.J., Anandan P. A framework for the robust estimation of optical flow// ICCV’93, May. – 1993. - P. 231 - 236.

5. Кузнецов П.К., Мартемьянов Б.В., Семавин В.И., Чекотило Е.Ю. Метод определения вектора скорости движения подстилающей поверхности// Вестник Самарского государственного технического университета. Серия Технические науки. – 2008. - № 2(22). – С. 96 - 110.

6. Кузнецов П.К., Чекотило Е.Ю., Мартемьянов Б.В. Исследование сходимости итерационной процедуры определения параметров движения изображений методом функционализации// Вестник Самарского государственного технического университета. Серия Технические науки. – 2010. - №2(26). – С. 80 - 85.